Illustrative Math Alignment: Grade 7 Unit 4

Proportional Relationships and Percentages

Lesson 10: Tax and Tip

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Nodes
Closed Captioned Video: Percents: Calculating Tax	Closed Captioned Video: Percents: Calculating Tax Topic Percents Description This video covers tax calculations for purchases, property, and VAT. Examples include grocery bills, iPad purchases, and real estate property taxes. Applications highlight the importance of understanding tax rates for budgeting and financial management.	Percents
Closed Captioned Video: Percents: Percent Decrease	Closed Captioned Video: Percents: Percent Decrease Topic Percents Description This video covers calculating percent decreases in scenarios such as price reductions, vehicle depreciation, and cube dimension changes. Examples demonstrate the relationship between linear decreases and their exponential effects on surface area and volume. Applications include consumer goods, real estate, and geometry.	Percents
Closed Captioned Video: Percents: Percent Increase	Closed Captioned Video: Percents: Percent Increase Topic Percents Description The video explains how to calculate percent increases, focusing on changes in school enrollments, asset values, and cube dimensions. Examples highlight the non-linear effects of changes on surface area and volume. Applications include finance, education, and geometry, emphasizing understanding growth trends.	Percents
Definition--Financial Literacy--Capital Gains Tax	Capital Gains Tax Topic Financial Literacy Definition Capital gains tax is a tax on the profit realized from the sale of a non-inventory asset.	Numerical and Algebraic Expressions
Definition--Financial Literacy--Federal Income Tax	Federal Income Tax Topic Financial Literacy Definition Federal income tax is a tax levied by the government on the annual earnings of individuals, corporations, and other legal entities.	Numerical and Algebraic Expressions
Definition--Financial Literacy--Income Tax	Income Tax Topic Financial Literacy Definition Income tax is a tax levied by governments on personal income.	Numerical and Algebraic Expressions
Definition--Financial Literacy--State Income Tax	State Income Tax Topic Financial Literacy Definition State income tax is a tax levied by individual states on the income of residents and businesses operating within the state.	Numerical and Algebraic Expressions
Definition--Financial Literacy--Tax	Tax Topic Financial Literacy Definition Tax is a mandatory financial charge imposed by a government on individuals or entities to fund public expenditures. Description Taxes are essential for funding government operations and public services, such as infrastructure, education, and healthcare. Understanding taxes is crucial for personal financial planning and compliance with legal obligations. In real-world applications, taxes influence spending, saving, and investment decisions. Math education helps students understand how taxes are calculated and their impact on net income. A teacher might explain, "Taxes are money you pay to the government, which helps fund services like schools and roads."	Numerical and Algebraic Expressions
Definition--Financial Literacy--Tax Credit	Tax Credit Topic Financial Literacy Definition A tax credit is an amount that taxpayers can subtract directly from taxes owed to the government.	Numerical and Algebraic Expressions
Definition--Financial Literacy--Tax Deduction	Tax Deduction Topic Financial Literacy Definition A tax deduction is an expense that can be subtracted from gross income to reduce the amount of income that is subject to tax.	Numerical and Algebraic Expressions
Definition--Financial Literacy--Taxable Income	Taxable Income Topic Financial Literacy Definition Taxable income is the portion of an individual's or business's income that is subject to taxation after all deductions and exemptions are applied.	Numerical and Algebraic Expressions
Definition--Ratios, Proportions, and Percents Concepts--Calculating Tax	Calculating Tax Topic Ratios, Proportions, and Percents Definition Calculating tax involves determining the percentage amount to be added to the base price of a product or service. Description Calculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy. For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 50 × 0.08 = 4 Therefore, the total cost is	Applications of Ratios, Proportions, and Percents
INSTRUCTIONAL RESOURCE: Algebra Application: Cicada Cycles	INSTRUCTIONAL RESOURCE: Algebra Application: Cicada Cycles In this Algebra Application, students study the life cycles of 13- and 17-year cicadas, as well as the populations of bird predators. Students develop a mathematical model using spreadsheets and investigate why the prime number life cycles help the cicadas. The math topics covered include: Mathematical modeling, Data gathering and analysis, Percent increase and decrease, Prime numbers and composites. This real world application of math concepts will engage your students.	Applications of Ratios, Proportions, and Percents, Percents and Numerical Expressions
Math Clip Art--Ratios, Proportions, Percents--Percent Change 01	Math Clip Art--Ratios, Proportions, Percents--Percent Change 01 Topic Ratios, Proportions, and Percents Description The image introduces the concept of percent change with the formula: Percent Change = (New - Original) / Original * 100%. It establishes the formula as the foundation for understanding percent change throughout the sequence. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
Math Clip Art--Ratios, Proportions, Percents--Percent Change 02	Math Clip Art--Ratios, Proportions, Percents--Percent Change 02 Topic Ratios, Proportions, and Percents Description This image explains that percent increase measures the change from one number to a greater number. It provides context for when to apply the concept of percent increase in real-life scenarios. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
Math Clip Art--Ratios, Proportions, Percents--Percent Change 03	Math Clip Art--Ratios, Proportions, Percents--Percent Change 03 Topic Ratios, Proportions, and Percents Description This image highlights that the numerical increase is the difference between the new and original values. It adds clarity by breaking down the calculation into a numerical difference. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
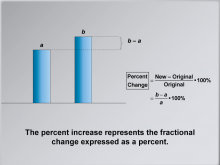
Math Clip Art--Ratios, Proportions, Percents--Percent Change 04	Math Clip Art--Ratios, Proportions, Percents--Percent Change 04 Topic Ratios, Proportions, and Percents Description This image demonstrates how numerical increase is represented as fractional change using the formula: (b - a) / a. It bridges numerical increase to fractional change, setting up for conversion to percent increase. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
Math Clip Art--Ratios, Proportions, Percents--Percent Change 05	Math Clip Art--Ratios, Proportions, Percents--Percent Change 05 Topic Ratios, Proportions, and Percents Description This image shows the formula for percent change as a fractional change expressed as a percentage: (b - a) / a * 100%. It reinforces the connection between fractional change and percent increase as part of the calculation process. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
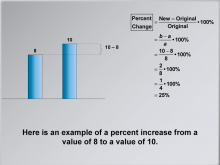
Math Clip Art--Ratios, Proportions, Percents--Percent Change 06	Math Clip Art--Ratios, Proportions, Percents--Percent Change 06 Topic Ratios, Proportions, and Percents Description This image provides an example of a percent increase calculation from 8 to 10, resulting in 25%. It offers a practical example to illustrate how the formula is applied to real numbers. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
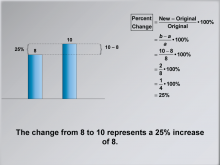
Math Clip Art--Ratios, Proportions, Percents--Percent Change 07	Math Clip Art--Ratios, Proportions, Percents--Percent Change 07 Topic Ratios, Proportions, and Percents Description This image reiterates the example calculation, emphasizing that the change from 8 to 10 is a 25% increase. It reinforces understanding by repeating the example with emphasis on the interpretation of the result. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
Math Clip Art--Ratios, Proportions, Percents--Percent Change 08	Math Clip Art--Ratios, Proportions, Percents--Percent Change 08 Topic Ratios, Proportions, and Percents Description This image defines percent decrease as the change from one number to a lesser number. It introduces the complementary concept of percent decrease to show both directions of percent change. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
Math Clip Art--Ratios, Proportions, Percents--Percent Change 09	Math Clip Art--Ratios, Proportions, Percents--Percent Change 09 Topic Ratios, Proportions, and Percents Description This image explains that numerical decrease is the difference between the new and original values. It mirrors the earlier explanation of numerical increase, ensuring consistency in presenting both cases. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
Math Clip Art--Ratios, Proportions, Percents--Percent Change 10	Math Clip Art--Ratios, Proportions, Percents--Percent Change 10 Topic Ratios, Proportions, and Percents Description This image demonstrates fractional change for a decrease using the formula: (b - a) / a. It completes the explanation of percent change by connecting numerical decrease to fractional representation. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
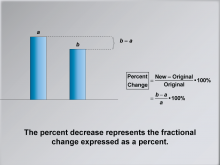
Math Clip Art--Ratios, Proportions, Percents--Percent Change 11	Math Clip Art--Ratios, Proportions, Percents--Percent Change 11 Topic Ratios, Proportions, and Percents Description This image explains that percent decrease represents fractional change expressed as a percentage: (b - a) / a * 100%. It extends the explanation to show how fractional change can be converted to percent decrease. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
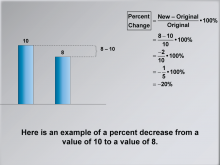
Math Clip Art--Ratios, Proportions, Percents--Percent Change 12	Math Clip Art--Ratios, Proportions, Percents--Percent Change 12 Topic Ratios, Proportions, and Percents Description This image provides an example of a percent decrease calculation from 10 to 8, resulting in -20%. It offers a practical example illustrating the application of the formula to calculate percent decrease. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
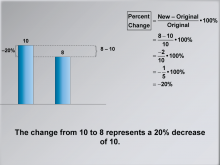
Math Clip Art--Ratios, Proportions, Percents--Percent Change 13	Math Clip Art--Ratios, Proportions, Percents--Percent Change 13 Topic Ratios, Proportions, and Percents Description This image reiterates the example, emphasizing that the change from 10 to 8 represents a 20% decrease. It reinforces understanding by summarizing the example with focus on the final interpretation of the result. Math clip art provides a visual and engaging way to explore complex mathematical concepts such as percent change. These examples illustrate how numbers, fractions, and percentages are interconnected, helping to build students' numerical reasoning skills.	Percents
Math Example--Math of Money--Calculating Tax--Example 1	Math Example--Math of Money--Calculating Tax--Example 1 Topic The Math of Money Description What is the tax due on a $1000 purchase when the sales tax rate is 5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations.	Percents
Math Example--Math of Money--Calculating Tax--Example 10	Math Example--Math of Money--Calculating Tax--Example 10 Topic The Math of Money Description What is the tax due on a $9999.99 purchase when the sales tax rate is 9.9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations.	Percents
Math Example--Math of Money--Calculating Tax--Example 2	Math Example--Math of Money--Calculating Tax--Example 2 Topic The Math of Money Description What is the tax due on a $1500 purchase when the sales tax rate is 6%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations.	Percents
Math Example--Math of Money--Calculating Tax--Example 3	Math Example--Math of Money--Calculating Tax--Example 3 Topic The Math of Money Description What is the tax due on a $2550 purchase when the sales tax rate is 7%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations.	Percents
Math Example--Math of Money--Calculating Tax--Example 4	Math Example--Math of Money--Calculating Tax--Example 4 Topic The Math of Money Description What is the tax due on a $999 purchase when the sales tax rate is 8%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations.	Percents
Math Example--Math of Money--Calculating Tax--Example 5	Math Example--Math of Money--Calculating Tax--Example 5 Topic The Math of Money Description What is the tax due on a $999.99 purchase when the sales tax rate is 9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations.	Percents
Math Example--Math of Money--Calculating Tax--Example 6	Math Example--Math of Money--Calculating Tax--Example 6 Topic The Math of Money Description What is the tax due on a $1250 purchase when the sales tax rate is 6.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations.	Percents
Math Example--Math of Money--Calculating Tax--Example 7	Math Example--Math of Money--Calculating Tax--Example 7 Topic The Math of Money Description What is the tax due on a $1399 purchase when the sales tax rate is 7.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations.	Percents
Math Example--Math of Money--Calculating Tax--Example 8	Math Example--Math of Money--Calculating Tax--Example 8 Topic The Math of Money Description What is the tax due on a $1575.50 purchase when the sales tax rate is 8.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations.	Percents
Math Example--Math of Money--Calculating Tax--Example 9	Math Example--Math of Money--Calculating Tax--Example 9 Topic The Math of Money Description What is the tax due on a $1999.99 purchase when the sales tax rate is 9.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations.	Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 1	Math Example--Math of Money--Calculating Tips and Commissions--Example 1 Topic The Math of Money Description Calculate a 15% tip on a $50 restaurant bill. The problem requires finding 15% of 50. To calculate the tip, multiply the cost (50) by the tip rate (0.15). Tip = 50 * 0.15 = 7.50. The answer is $7.50. In general, the topic 'The Math of Money' covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved.	Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 10	Math Example--Math of Money--Calculating Tips and Commissions--Example 10 Topic The Math of Money Description Calculate a 9.5% sales commission on a $350,999 sale. The problem requires finding 9.5% of 350,999. To calculate the commission, multiply the sale amount (350,999) by the commission rate (0.095). Commission = 350,999 * 0.095 ≈ 33,344.91. The answer is approximately $33,344.91.	Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 2	Math Example--Math of Money--Calculating Tips and Commissions--Example 2 Topic The Math of Money Description Calculate a 16% tip on a $55 restaurant bill. The problem requires finding 16% of 55. To calculate the tip, multiply the cost (55) by the tip rate (0.16). Tip = 55 * 0.16 = 8.8. The answer is $8.80. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved.	Percents
Math Example--Math of Money--Calculating Tips and Commissions--Example 3	Math Example--Math of Money--Calculating Tips and Commissions--Example 3 Topic The Math of Money Description Calculate an 18% tip on a $75.50 restaurant bill. The problem requires finding 18% of 75.50. To calculate the tip, multiply the cost (75.50) by the tip rate (0.18). Tip = 75.50 * 0.18 = 13.59. The answer is $13.59. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved.	Percents

Illustrative Math Alignment: Grade 7 Unit 4

Proportional Relationships and Percentages

Lesson 10: Tax and Tip

Topic

Description

Topic

Description

Topic

Description

Topic

Definition

Topic

Definition

Topic

Definition

Topic

Definition

Topic

Definition

Description

Topic

Definition

Topic

Definition

Topic

Definition

Topic

Definition

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic

Description

Topic