Illustrative Math Alignment: Grade 7 Unit 5

Topic

Rational Functions

Topic

Inequalities

Description

This video models an inequality to explain how floodgates in Venice prevent flooding during storms. The key concept is the activation threshold, where the water level exceeds a critical value. Vocabulary includes inequality, threshold, variable, and model. Using a TI-Nspire, the video demonstrates creating a random variable for water levels and a function to evaluate if floodgates should activate. It illustrates real-world applications in engineering and environmental management.

Topic

Rational Functions

Topic

Rational Functions

Description

Explains submarine pressure and volume relationships using rational functions, illustrating depth impacts on vessel integrity and scuba safety.

This video provides a detailed explanation of explains submarine pressure and volume relationships using rational functions, illustrating depth impacts on vessel integrity and scuba safety. and its significance in understanding rational functions.

Topic

Rational Functions

Description

Examines surface area to volume ratios in animals using rational functions, connecting these ratios to evolutionary adaptations in different climates.

This video provides a detailed explanation of examines surface area to volume ratios in animals using rational functions, connecting these ratios to evolutionary adaptations in different climates and its significance in understanding rational functions.

Topic

Rational Functions

Description

Demonstrates the optics of the Hubble telescope through rational functions, analyzing lens properties and asymptotes for image clarity.

This video provides a detailed explanation of demonstrates the optics of the Hubble telescope through rational functions, analyzing lens properties and asymptotes for image clarity and its significance in understanding rational functions.

After briefly reviewing the concept of inverse variation, this video explores Boyle’s law, a real world example of an inversely proportional relationship between pressure and volume of a gas. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, it goes on to examine similarities and differences among rational functions and numbers. Finally, it takes a look at rational functions graphs and ends with a delightful example merging Euclidean and analytic geometry, thanks to the TI-Nspire technology. Concepts explored: functions, rational expressions, rational functions, asymptotes

In this Investigation we look at an application of rational functions: Boyle's Law. This video is Segment 1 of a 4 segment series related to Algebra Nspirations: Rational Functions and Expressions. Segments 1 and 2 are grouped together.

In this Investigation we look at graphs of rational functions. This video is Segment 3 of a 4 segment series related to Algebra Nspirations: Rational Functions and Expressions. Segments 3 and 4 are grouped together.

In this TI Nspire tutorial, the Graph window is used to create a slider-based graph of a rational function. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. .

Topic

Ratios

Description

This video covers converting units using rates, with examples like speed conversion, currency exchange, and calculating seconds in a year. It emphasizes multiplication by conversion rates to transition between units effectively.

Topic

Ratios

Description

Rates are linked to slopes in linear functions. The video explores calculating rates of change for graphs of speed, savings growth, and loan repayment. It highlights using the slope formula to interpret and solve practical problems.

Topic

Ratios

Description

This video demonstrates calculating rates from data sets, focusing on patterns like distance-time relationships and wages. Examples include determining car speeds, hourly wages, and unit costs of gasoline. Data tables are used to visualize and compute rates.

Topic

Ratios

Description

The video explores working with ratios involving decimals, such as finding unit costs for salmon or recycling rates. Scientific notation and multi-step conversions are used to calculate speeds of spacecraft like Voyager I.

Topic

Ratios

Description

Ratios are connected to percentages in this video. Examples include finding percentages of colored socks or non-green items in collections. It develops a formula for converting part-to-whole ratios into percentages.

Topic

Ratios

Description

The video focuses on unit rates, where the denominator equals one. It includes practical examples like finding the cost per pound of bananas or determining hourly wages. Applications extend to conversions and scaling calculations for various real-world tasks.

Topic

Ratios

Description

This video illustrates converting ratios to percents using visual aids like area models and grids. Examples include determining percentages of colored eggs, fruit types, and combinations of colored lights.

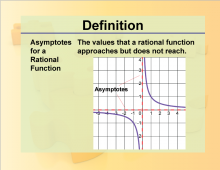
Topic

Rationals and Radicals

Definition

An asymptote is a line that a graph approaches but never touches.

Description

Asymptotes are significant in the study of Rational Numbers, Expressions, Equations, and Functions. They help in understanding the behavior of graphs of rational functions, particularly as the values of the variables approach certain limits. Horizontal asymptotes indicate the value that the function approaches as the input grows infinitely large or small. Vertical asymptotes show the values that the function cannot take because they cause division by zero.

Topic

Rationals and Radicals

Definition

An extraneous solution is a solution derived from an equation that is not a valid solution to the original equation.

Description

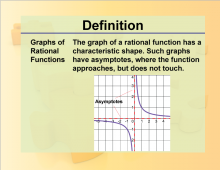
Extraneous solutions often arise in the context of Rational and Radical Equations. They are solutions that appear during the process of solving an equation but do not satisfy the original equation. This can happen when both sides of an equation are squared or when other operations introduce additional solutions.

Topic

Rationals and Radicals

Definition

Graphs of rational functions are visual representations of equations involving rational expressions.

Description

Graphs of rational functions are fundamental in the study of Rational Numbers, Expressions, Equations, and Functions. They help in understanding the behavior of these functions, including their asymptotes, intercepts, and regions of increase and decrease.

Topic

Rationals and Radicals

Definition

A horizontal asymptote is a horizontal line that a rational function graph approaches as the input values become very large or very small.

Description

Horizontal asymptotes are an important concept in the study of Rational Numbers, Expressions, Equations, and Functions. They indicate the value that a function approaches as the input grows infinitely large or small. Understanding horizontal asymptotes is crucial for graphing rational functions accurately and for analyzing their long-term behavior.

Topic

Rationals and Radicals

Definition

Inverse variation describes a relationship between two variables in which the product is a constant. When one variable increases, the other decreases proportionally.

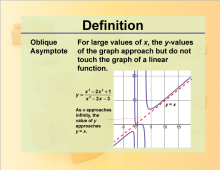
Topic

Rationals and Radicals

Definition

An oblique asymptote is a diagonal line that the graph of a function approaches as the input values become very large or very small.

Description

Oblique Asymptotes are important in the study of Rational Numbers, Expressions, Equations, and Functions. They occur in rational functions where the degree of the numerator is one more than the degree of the denominator. For example, the function 

$$f(x) = \frac{x^2 + 1}{x}$$

Topic

Rationals and Radicals

Definition

Rational equations are equations that involve rational expressions, which are fractions containing polynomials in the numerator and denominator.

Description

Rational Equations are a fundamental aspect of Rational Numbers, Expressions, Equations, and Functions. These equations involve rational expressions, which are fractions containing polynomials in the numerator and denominator. Solving rational equations typically requires finding a common denominator, clearing the fractions, and then solving the resulting polynomial equation. For example, to solve 

$$\frac{1}{x} + \frac{1}{x+1} = \frac{1}{2}$$

Topic

Rationals and Radicals

Definition

Rational functions are functions that are the ratio of two polynomials.

Description

Rational Functions are a key concept in the study of Rational Numbers, Expressions, Equations, and Functions. These functions are the ratio of two polynomials, such as 

$$f(x) = \frac{P(x)}{Q(x)}$$

where P(x) and Q(x) are polynomials. Understanding rational functions involves analyzing their behavior, including identifying asymptotes, intercepts, and discontinuities. For example, the function 

$$f(x) = \frac{1}{x}$$

Topic

Rationals and Radicals

Definition

Rational numbers are numbers that can be expressed as a ratio of two integers, where the denominator is not zero.

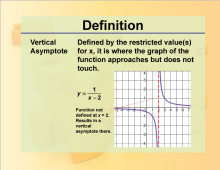
Topic

Rationals and Radicals

Definition

A vertical asymptote is a vertical line that the graph of a function approaches but never reaches as the input values get closer to a certain point.

Description

Vertical Asymptotes are a crucial concept in the study of Rational Numbers, Expressions, Equations, and Functions. They occur in rational functions when the denominator equals zero for certain input values, causing the function to approach infinity or negative infinity. For example, the function 

$$f(x) = \frac{1}{x-2}$$

Topic

Ratios, Proportions, and Percents

Definition

Calculating tax involves determining the percentage amount to be added to the base price of a product or service.

Description

Calculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy.

For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 

50 × 0.08 = 4

Therefore, the total cost is 

Topic

Ratios, Proportions, and Percents

Definition

Calculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill.

Description

Calculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. 

For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 

80 × 0.15 = 12

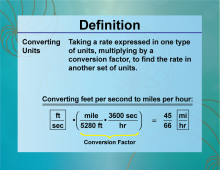
Topic

Ratios, Proportions, and Percents

Definition

Converting units involves changing a measurement from one unit to another using a conversion factor.

Description

Converting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters.

For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 

5 × 1.60934 = 8.0467 kilometers

Topic

Ratios, Proportions, and Percents

Definition

Dimensional analysis is a method used to convert one unit of measurement to another using conversion factors.

Description

Dimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit.

For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors  1 meter = 0.001 kilometers and 1 hour = 3600 seconds: 

Topic

Ratios, Proportions, and Percents

Definition

Equivalent ratios are ratios that express the same relationship between quantities.

Description

Equivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models.

For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced.

Topic

Ratios, Proportions, and Percents

Definition

Part-to-part ratios compare different parts of a whole to each other.

Description

Part-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics.

For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3.

Topic

Ratios, Proportions, and Percents

Definition

Part-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions.

Description

Part-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making.

Topic

Ratios, Proportions, and Percents

Definition

A percent is a ratio that compares a number to 100.

Description

Percentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates.

For example, if you score 45 out of 50 on a test, your percentage score is 

(45/50) × 100 = 90%

Topic

Ratios, Proportions, and Percents

Definition

Percent decrease measures the reduction in value expressed as a percentage of the original value.

Description

Percent decrease is used to quantify the reduction in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as price reductions and weight loss.

For example, if the price of a jacket drops from $80 to $60, the percent decrease is calculated as 

(80 − 60)/80 × 100 = 25%.

Topic

Ratios, Proportions, and Percents

Definition

Percent increase measures the growth in value expressed as a percentage of the original value.

Description

Percent increase is used to quantify the growth in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as salary increases and population growth.

For example, if the price of a stock rises from \$50 to \$75, the percent increase is calculated as 

(75 − 50)/50 × 100 = 50%

Topic

Ratios, Proportions, and Percents

Definition

Percent of a number involves calculating the amount represented by a certain percentage of that number.

Description

Understanding percentages is crucial for working with finances, statistics, and data analysis. For instance, to find 20% of 50, multiply 50 by 0.20, resulting in 10. Likewise, it's important for everyday scenarios, such as calculating discounts during shopping.

Topic

Ratios, Proportions, and Percents

Definition

Percent of an unknown refers to solving for an unknown quantity when given a percentage of that quantity.

Description

Knowing how to find a percentage of an unknown variable is essential for solving equations in algebra. This concept appears in various situations, such as when determining discounts or portions of a total amount.

For instance, if 20% of an unknown number equals 15, you can set up the equation: 

0.20x = 15

Topic

Ratios, Proportions, and Percents

Definition

Percents as decimals involve converting a percentage into its decimal representation.

Description

Converting percents to decimals is a key skill in mathematics, allowing students to perform calculations involving percentages more easily. To convert, divide the percent by 100.

For example, 75% as a decimal is 0.75, calculated by dividing 75 by 100. This conversion is useful in many contexts, such as finance, where calculations are conducted using decimal values. Mastering this concept enables students to approach real-world problems with greater confidence and accuracy.

Topic

Ratios, Proportions, and Percents

Definition

A proportion is an equation that states that two ratios are equal.

Description

Understanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models.

To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio.

Topic

Ratios, Proportions, and Percents

Definition

Proportional refers to the relationship between two quantities where their ratio is constant.

Description

Proportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering.

For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations.

Topic

Ratios, Proportions, and Percents

Definition

A rate is a ratio that compares two quantities with different units.

Description

Rates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting.

For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems.

Topic

Ratios, Proportions, and Percents

Definition

A ratio is a comparison of two quantities by division.

Description

Ratios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance.

For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations.

Topic

Ratios, Proportions, and Percents

Definition

Ratios and fractions are both ways of comparing quantities, with fractions representing a part of a whole.

Description

Understanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio.

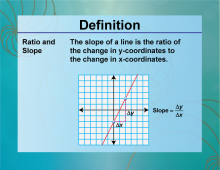
Topic

Ratios, Proportions, and Percents

Definition

The slope of a line is a ratio that represents the change in y over the change in x.

Description

Understanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points.

For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields.

Topic

Ratios, Proportions, and Percents

Definition

Ratios in simplest form are ratios that have been reduced to their smallest whole number terms.

Description

Reducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1.

For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities.

Topic

Ratios, Proportions, and Percents

Definition

Ratios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers.

Description

Ratios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons.

Topic

Ratios, Proportions, and Percents

Definition

Ratios with fractions compare two quantities where one or both of the quantities are fractions.

Description

Ratios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4.

Topic

Ratios, Proportions, and Percents

Definition

Ratios with percents involve comparing quantities where one or both of the quantities are expressed as percentages.

Description

Ratios with percents are widely used in various fields, including finance, statistics, and everyday life. For example, when comparing interest rates, growth rates, or discount rates, percentages are often used. Understanding these ratios allows for better financial decision-making and data analysis.