
Illustrative Math Alignment: Grade 7 Unit 7
Angles, Triangles, and Prisms
Lesson 15: Distinguishing Volume and Surface Area
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
VIDEO: 3D Geometry Animation: Antiprism | VIDEO: 3D Geometry Animation: Antiprism
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Triangular Prisms |

|
VIDEO: 3D Geometry Animation: Rectangular Prism | VIDEO: 3D Geometry Animation: Rectangular Prism
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Rectangular Prisms |

|
VIDEO: 3D Geometry Animation: Triangular Prism | VIDEO: 3D Geometry Animation: Triangular Prism
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Antiprism | AntiprismTopic3D Geometry DescriptionThis animated clip art image of an Antiprism illustrates its geometric properties by showing its two parallel, congruent polygonal faces connected by an alternating band of triangles. This animation helps visualize the symmetry and rotational aspects of the shape, making it an excellent tool for teaching concepts related to 3D geometry. Animated math clip art like this antiprism is crucial for teaching as it enables students to see abstract concepts in motion, enhancing understanding and engagement. Teachers can use this image to demonstrate how antiprisms are constructed and explore their properties interactively. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Antiprism with Horizontal Cross-Section | Antiprism with Horizontal Cross-SectionTopic3D Geometry DescriptionThis animation shows an antiprism with a horizontal cross-section, revealing its internal structure when sliced parallel to its bases. This visualization aids in understanding the spatial relationships and symmetry within the antiprism, making it a valuable teaching tool for discussing cross-sections and geometry. Using animated math clip art like this helps students grasp complex spatial concepts by breaking them down into visual components. Teachers can use this image to explain how cross-sections can provide insight into the internal geometry of polyhedra. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Antiprism with Vertical Cross-Section | Antiprism with Vertical Cross-SectionTopic3D Geometry DescriptionThis animation depicts an antiprism with a vertical cross-section, showing its internal structure when sliced perpendicular to its bases. This view is essential for understanding the vertical symmetry and arrangement of triangular faces, providing a deeper insight into the geometry of antiprisms. Animated math clip art like this is important for teaching as it allows students to visualize and explore the internal structures of complex shapes dynamically. Teachers can use this image to discuss how vertical cross-sections reveal different aspects of a shape's geometry. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Horizontal Cross-Section of a Rectangular Prism | Animated Math Clip Art: Horizontal Cross-Section of a Rectangular Prism This animated math clip art illustrates how a horizontal plane intersects a rectangular prism, forming a two-dimensional cross-section. As the plane moves through the prism, students can observe that the resulting cross-section is always a rectangle, reinforcing key geometric concepts related to slicing three-dimensional shapes. Ideal for classroom instruction, this GIF animation helps students develop spatial reasoning by demonstrating how horizontal slices interact with the structure of a rectangular prism. This visual aid is particularly useful for teaching cross-sections in geometry, emphasizing how different slicing directions produce distinct 2D shapes. |
Rectangular Prisms |

|
Animated Math Clip Art--3D Geometry--Net for Antiprism | Net for AntiprismTopic3D Geometry DescriptionThis animation shows the net of an antiprism unfolding and folding. A net is a 2D representation of a 3D shape that, when folded, creates the 3D object. For an antiprism, this includes two polygonal bases and a band of triangles. Animated math clip art like this is invaluable for teaching as it helps students visualize the transition between 2D and 3D representations. Teachers can use this to explain concepts of surface area, shape properties, and spatial reasoning. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Net for Rectangular Prism | Net for Rectangular PrismTopic3D Geometry DescriptionThis animation shows the net of a rectangular prism folding into the rectangular prism. A rectangular prism's net consists of six rectangles: two identical pairs of congruent rectangles for the sides, and another pair for the top and bottom. Animated math clip art like this is crucial for teaching as it helps students visualize how 2D shapes form 3D objects. Teachers can use this to explain concepts of surface area, volume, and the properties of prisms. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Net for Triangular Prism | Net for Triangular PrismTopic3D Geometry DescriptionThis animation shows the net of a triangular prism folding into the triangular prism. A triangular prism's net consists of two triangular bases and three rectangular faces that form the lateral surface. Animated math clip art like this is crucial for teaching as it helps students visualize how 2D shapes form 3D objects. Teachers can use this to explain concepts of surface area, volume, and the properties of prisms. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Rectangular Prism | Rectangular PrismTopic3D Geometry DescriptionThis animation shows a rectangular prism, a three-dimensional figure with six rectangular faces. It's a fundamental shape in geometry, with applications in volume and surface area calculations. Animated math clip art like this is essential for teaching as it allows students to visualize 3D shapes from different angles. Teachers can use this to explain concepts of volume, surface area, and properties of prisms. Here's a potential script for teachers: "Observe this rectangular prism. Notice how it has six rectangular faces. How would you calculate its volume? Its surface area? How does this shape relate to real-world objects?" |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Triangular Prism | Triangular PrismTopic3D Geometry DescriptionThis animation depicts a triangular prism, a three-dimensional shape with two triangular bases and three rectangular faces. It's an important shape in geometry with various real-world applications. Using animated math clip art like this helps students visualize 3D shapes from different angles. Teachers can use this to explain concepts of volume, surface area, and properties of prisms. Here's a potential script for teachers: "Observe this triangular prism. Can you identify its bases and lateral faces? How would you calculate its volume and surface area? Can you think of any objects in real life that have this shape?" |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Triangular Prism with Horizontal Cross-Section | Triangular Prism with Horizontal Cross-SectionTopic3D Geometry DescriptionThis animation shows a triangular prism with a horizontal cross-section. It illustrates that slicing the prism parallel to its base results in a rectangular cross-section that varies in size depending on the location of the slice. Animated math clip art like this helps students understand the internal structure of prisms. Teachers can use this to discuss concepts such as congruence, cross-sectional area, and how this relates to the volume of a prism. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Triangular Prism with Vertical Cross-Section | Triangular Prism with Vertical Cross-SectionTopic3D Geometry DescriptionThis animation depicts a triangular prism with a vertical cross-section. It shows how slicing the prism vertically results in a triangular cross-section, and all such triangles are congruent along the length of the prism. Using animated math clip art like this provides students with a different perspective on the internal geometry of prisms. Teachers can use this to discuss concepts such as height, lateral area, and how vertical cross-sections relate to the surface area of a prism. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Vertical Cross-Section of a Rectangular Prism | Animated Math Clip Art: Vertical Cross-Section of a Rectangular Prism This animated math clip art visually demonstrates how a vertical plane intersects a rectangular prism, producing a two-dimensional cross-section. As the plane moves through the 3D shape, students can observe how the resulting cross-section remains a rectangle, reinforcing key geometric concepts related to slicing three-dimensional figures. Perfect for classroom instruction, this GIF animation helps students develop spatial reasoning by illustrating how a vertical slice interacts with the faces of a rectangular prism. This resource is particularly useful for teaching cross-sections in geometry and preparing students to understand more complex 3D slicing concepts. |
Rectangular Prisms |

|
Closed Captioned Video: Geometry Applications--Antiprisms | Closed Captioned Video: Geometry Applications--Antiprisms
In this video students learn the basics of antiprisms, in the context of New York’s Freedom Tower, which has an antiprism design. They learn the properties of antiprisms, with the focus on those with a square base. |
Rectangular Prisms |

|
Closed Captioned Video: Geometry Applications--Rectangular Prisms | Closed Captioned Video: Geometry Applications--Rectangular Prisms
In this video students learn the basics of rectangular prisms, in the context of a New York residential tower: 432 Park Avenue. They learn the properties of rectangular prisms, with and without square bases, and the architectural requirements that influence the use of both types of rectangular prisms. |
Rectangular Prisms |

|
Closed Captioned Video: Geometry Applications--Triangular Prisms | Closed Captioned Video: Geometry Applications--Triangular Prisms
In this video students study a real-world application of triangular prisms: The Flat Iron Building in New York City. This building is an ideal example of a real-world prism and also provides a tie-in to right triangle geometry. This video describes the geometry of the Flat Iron Building, as well as its architecture. It includes animations that demonstrate the key features of triangular prisms. |
Triangular Prisms |

|
Closed Captioned Video: Geometry Applications--What Are Prisms? | Closed Captioned Video: Geometry Applications--What Are Prisms?
In this video students learn the basics of prisms and anti prisms. They learn the properties of triangular prisms, rectangular prisms, triangular antiprisms, and rectangular antiprisms. |
Rectangular Prisms and Triangular Prisms |
|
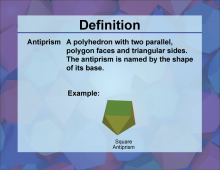
Definition--3D Geometry Concepts--Antiprism | AntiprismTopic3D Geometry DefinitionAn antiprism is a polyhedron composed of two parallel copies of an n-sided polygon, connected by an alternating band of triangles. DescriptionAntiprisms are fascinating three-dimensional geometric figures that play a significant role in the study of polyhedra and spatial geometry. Unlike prisms, which have rectangular lateral faces, antiprisms feature triangular faces connecting their two parallel polygonal bases. This unique structure gives antiprisms distinct properties and applications in various fields of mathematics and engineering. |
3-Dimensional Figures |
|
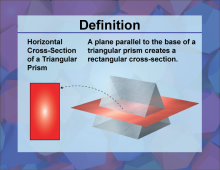
Definition--3D Geometry Concepts--Horizontal Cross-Sections of a Triangular Prism | Horizontal Cross Sections of a Triangular PrismTopic3D Geometry DefinitionA horizontal cross-section of a triangular prism is the shape obtained by cutting the prism with a plane parallel to its base. DescriptionIn three-dimensional geometry, a cross-section is the intersection of a plane with a solid figure. When this plane is parallel to the base of the solid, the resulting shape is called a horizontal cross-section. For a triangular prism with a rectangular base, this cross-section will always be a rectangle, similar in shape to the base of the prism. |
Triangular Prisms |
|
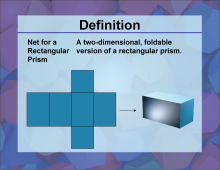
Definition--3D Geometry Concepts--Net for a Rectangular Prism | Net for a Rectangular PrismTopic3D Geometry DefinitionA net for a rectangular prism is a two-dimensional representation that, when folded, forms a three-dimensional rectangular prism. DescriptionIn the realm of three-dimensional geometry, the concept of a net is crucial for understanding how 3D shapes are constructed from 2D figures. A net for a rectangular prism is essentially a layout of all the faces of the prism in a single plane. This layout includes six rectangles that correspond to the six faces of the prism. By folding along the edges of these rectangles, one can recreate the three-dimensional shape of the rectangular prism. |
Rectangular Prisms |
|
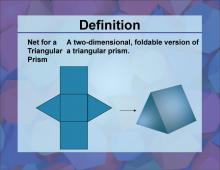
Definition--3D Geometry Concepts--Net for a Triangular Prism | Net for a Triangular PrismTopic3D Geometry DefinitionA net for a triangular prism is a two-dimensional figure that can be folded to form the surface of a three-dimensional triangular prism. DescriptionIn the context of three-dimensional geometry, a net is a crucial concept for understanding the surface area and structure of 3D shapes. Specifically, the net for a triangular prism consists of two triangular faces and three rectangular faces. When these faces are arranged in a specific two-dimensional pattern, they can be folded along the edges to form a triangular prism. |
Triangular Prisms |
|
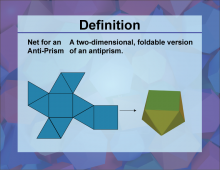
Definition--3D Geometry Concepts--Net for an Antiprism | Net for an AntiprismTopic3D Geometry. DefinitionA net for an antiprism is a two-dimensional shape that can be folded to form a three-dimensional antiprism, which is a type of polyhedron with two parallel polygonal bases connected by an alternating band of triangles. DescriptionIn the realm of three-dimensional geometry, an antiprism is a fascinating polyhedron that extends the concept of prisms. Unlike regular prisms, which have two parallel bases connected by rectangular faces, antiprisms have two parallel bases connected by an alternating band of triangles. This unique structure results in a more complex and often more visually interesting shape. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Prism | PrismTopic3D Geometry DefinitionA prism is a three-dimensional solid object with two identical polygonal bases connected by parallelogram faces. DescriptionIn the realm of three-dimensional geometry, a prism is a polyhedron with two parallel, congruent bases connected by rectangular or parallelogram faces. The defining characteristic of a prism is that its cross-sections parallel to the bases are identical to the bases themselves. This property makes prisms a significant topic of study in geometry. |
3-Dimensional Figures |
|
Definition--3D Geometry Concepts--Rectangular Prism | Rectangular PrismTopic3D Geometry DefinitionA rectangular prism is a three-dimensional figure with six rectangular faces, where opposite faces are congruent and parallel. DescriptionThe rectangular prism is a fundamental shape in three-dimensional geometry, serving as a building block for understanding more complex 3D structures. It is characterized by its three dimensions: length, width, and height, which are clearly labeled in the image. This shape is ubiquitous in both natural and man-made environments, making it a crucial concept for students to grasp. |
Rectangular Prisms |
|
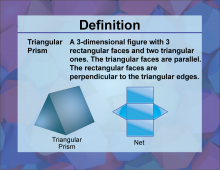
Definition--3D Geometry Concepts--Triangular Prism | Triangular PrismTopic3D Geometry DefinitionA triangular prism is a three-dimensional geometric solid with two congruent triangular bases and three rectangular faces. DescriptionThe triangular prism is a fundamental shape in three-dimensional geometry, playing a crucial role in understanding the properties of polyhedra and their applications in various fields. This prism is characterized by its unique structure, consisting of two parallel triangular bases connected by three rectangular faces. The shape of the triangular bases can vary, allowing for right, equilateral, isosceles, or scalene triangular prisms. |
Triangular Prisms |
|
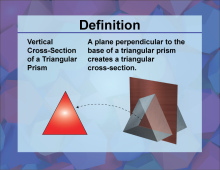
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Triangular Prism | Vertical Cross Sections of a Triangular PrismTopic3D Geometry DefinitionA vertical cross section of a triangular prism is a two-dimensional shape obtained by slicing the prism parallel to its height, revealing a triangular face. |
Triangular Prisms |

|
Definition--Geometry Basics--Antiprism | AntiprismTopicGeometry Basics DefinitionA polyhedron with two parallel faces and other faces that are triangular. DescriptionAn antiprism is a type of polyhedron that has two parallel faces connected by an alternating band of triangles. This geometric shape is significant in advanced geometry and has applications in fields such as crystallography and molecular chemistry. Understanding antiprisms helps in comprehending the properties of polyhedra and their role in three-dimensional space. For example, the volume of an antiprism can be calculated using specific geometric formulas, making it a useful concept in various scientific and mathematical applications. |
3-Dimensional Figures |

|
Definition--Geometry Basics--Prism | PrismTopicGeometry Basics DefinitionA prism is a solid shape with two parallel, congruent bases connected by rectangular or parallelogram faces. DescriptionPrisms are significant in the study of three-dimensional shapes. They have a uniform cross-section, allowing for easy calculations of volume and surface area. The volume can be calculated with the formula V = B⋅h where B is the area of the base and h is the height. Prisms are commonly encountered in real-world applications such as packaging and structural designs, making them an essential concept in geometry. |
3-Dimensional Figures |
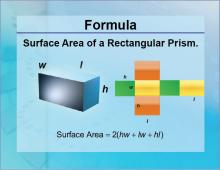
|
Formulas--Surface Area of a Rectangular Prism | Formulas--Surface Area of a Rectangular Prism
The formula for the Surface Area of a Rectangular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
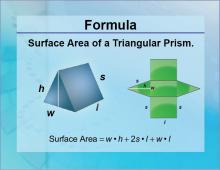
|
Formulas--Surface Area of a Triangular Prism | Formulas--Surface Area of a Triangular Prism
The formula for the Surface Area of a Triangular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area |
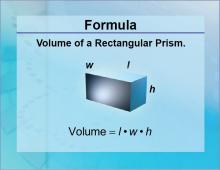
|
Formulas--Volume of a Rectangular Prism | Formulas--Volume of a Rectangular Prism
The formula for the Volume of a Recantular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |
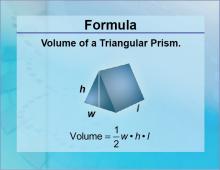
|
Formulas--Volume of a Triangular Prism | Note: The download is a JPG file. Related ResourcesTo see the complete collection of Formulas, click on this link: https://media4math.com/math-formulas |
Volume |

|
Google Earth Voyager Story: Architectural Prisms, Part 1 | Google Earth Voyager Story: Architectural Prisms, Part 1TopicGeometric Models |
Triangular Prisms |

|
Google Earth Voyager Story: Architectural Prisms, Part 2 | Google Earth Voyager Story: Architectural Prisms, Part 2TopicGeometric Models |
Rectangular Prisms |

|
Google Earth Voyager Story: Architectural Prisms, Part 3 | Google Earth Voyager Story: Architectural Prisms, Part 3
In this Google Earth Voyager story visit architectural landmarks in New York City to learn about the geometry of prisms. In this lesson, visit the Freedom Tower in Lower Manhattan and learn about antiprisms. Then build a scale model of the Freedom Tower. This is part of a collection of Google Earth Voyager Stories that use Google's mapping technology to explore relevant math stories. To see the complete collection of the Google Earth Voyager Stories, click on this link. Note: The download is the teacher's guide.Viewing Media4Math Stories on Google EarthThese Google Earth Voyager Stories are also available on Google Earth. Best viewed in Chrome, click on the links below to view these dynamic stories using Google's technology: |
3-Dimensional Figures |

|
Math Clip Art--3D Figures--Rectangular Prism | Math Clip Art--3D Figures--Rectangular Prism
This collection of clip art images includes images of 3D figures and composite figures. |
Definition of a Quadrilateral |

|
Math Clip Art--3D Figures--Triangular Prism | Math Clip Art--3D Figures--Triangular Prism
This collection of clip art images includes images of 3D figures and composite figures. |
3-Dimensional Figures |
|
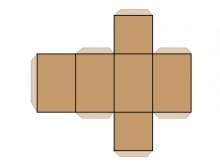
Math Clip Art--Net for a Rectangular Prism | Math Clip Art--Net for a Rectangular PrismTopicGeometry DescriptionThis math clip art image is part of a series showcasing 2D nets of 3D figures, specifically illustrating the net for a rectangular prism. The image displays a flattened representation of a rectangular prism, consisting of six connected rectangles arranged in a cross-like pattern. This visual aid is crucial for students to understand how a 3D rectangular prism can be unfolded into a 2D shape. |
3-Dimensional Figures |
|
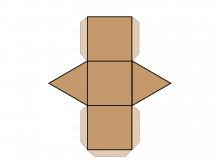
Math Clip Art--Net for a Triangular Prism | Math Clip Art--Net for a Triangular PrismTopicGeometry DescriptionThis math clip art image is part of a series illustrating 2D nets of 3D figures, with this particular image focusing on the net for a triangular prism. The image shows a flattened representation of a triangular prism, consisting of two triangular bases and three rectangular faces. This visual aid is essential for students to comprehend how a 3D triangular prism can be unfolded into a 2D pattern. |
3-Dimensional Figures |
|
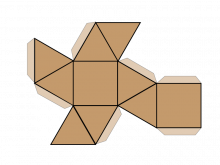
Math Clip Art--Net for an Antiprism | Math Clip Art--Net for an AntiprismTopicGeometry DescriptionThis math clip art image is part of a series showcasing 2D nets of 3D figures, specifically illustrating the net for an antiprism. The image displays a flattened representation of an antiprism, consisting of two polygonal bases (typically regular polygons) connected by a band of triangles. This visual aid is crucial for students to understand how a 3D antiprism can be unfolded into a 2D shape. |
3-Dimensional Figures |
|
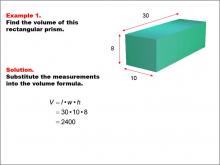
Math Example--Volume Concepts--Calculating Volume: Example 1 | Math Example--Volume Concepts--Calculating Volume: Example 1TopicVolume DescriptionA rectangular prism with dimensions labeled: length = 30, width = 10, and height = 8. The image shows how to find the volume of the prism using the formula for volume of a rectangular prism. This image illustrates Example 1: The caption explains how to calculate the volume of the rectangular prism using the formula V = l * w * h. The given dimensions are substituted into the formula: V = 30 * 10 * 8 = 2400.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 10 | Math Example--Volume Concepts--Calculating Volume: Example 10TopicVolume DescriptionA green cylinder with a general radius y and height x. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 10: The task is to find the volume of this cylinder. The volume formula V = πr2h is used, and substituting r = y and h = x, the volume is calculated as V = xy2π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 11 | Math Example--Volume Concepts--Calculating Volume: Example 11TopicVolume DescriptionA hollow green cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 11: The task is to find the volume of this hollow cylinder. The volume formula for a hollow cylinder V = πr12h1 - πr22h2 is used. Substituting values, the result is V = 285π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 12 | Math Example--Volume Concepts--Calculating Volume: Example 12TopicVolume DescriptionA hollow green cylinder with an outer radius y, an inner radius y - 1, and a height x. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 12: The task is to find the volume of this hollow cylinder. Using V = π(r12h1 - r22h2), substituting values gives: V = πx(y2 - (y - 1)2= πx(2y - 1). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 13 | Math Example--Volume Concepts--Calculating Volume: Example 13TopicVolume DescriptionA rectangular-based pyramid is shown with dimensions: base length 10, base width 8, and height 30. The image demonstrates how to calculate the volume of this pyramid. This image illustrates Example 13: The caption provides a step-by-step solution for calculating the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h. Substituting values: V = (1/3) * 8 * 10 * 30 = 800. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 14 | Math Example--Volume Concepts--Calculating Volume: Example 14TopicVolume DescriptionA general rectangular-based pyramid is shown with variables x, y, and z representing the base dimensions and height. This example shows how to calculate the volume of a pyramid using variables instead of specific numbers. This image illustrates Example 14: The caption explains how to calculate the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h, which simplifies to V = (1/3) * x * y * z. |
Volume |
|
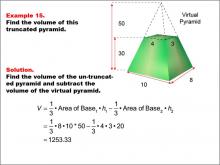
Math Example--Volume Concepts--Calculating Volume: Example 15 | Math Example--Volume Concepts--Calculating Volume: Example 15TopicVolume |
Volume |
|
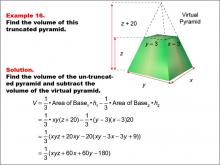
Math Example--Volume Concepts--Calculating Volume: Example 16 | Math Example--Volume Concepts--Calculating Volume: Example 16TopicVolume DescriptionA truncated rectangular-based pyramid is shown with variables x, y, and z representing dimensions. The smaller virtual pyramid has reduced dimensions by 3 units for both width and length and reduced height by z - 20. The image demonstrates how to calculate the volume in terms of variables. This image illustrates Example 16: The caption explains how to find the volume of a truncated pyramid using variables for both pyramids' dimensions. Formula: V = (1/3) * xy(z + 20) - (1/3) * (y - 3)(x - 3)(z), which simplifies to V = (1/3) * (xyz + 60x + 60y - 180). |
Volume |