
Illustrative Math Alignment: Grade 6 Unit 3
Unit Rates and Percentages
Lesson 13: Benchmark Percentages
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Example--Percents--Percent Change--Example 7 | Math Example--Percents--Percent Change--Example 7
This is part of a collection of math examples that focus on percents. |
Percents |

|
Math Example--Percents--Percent Change--Example 8 | Math Example--Percents--Percent Change--Example 8
This is part of a collection of math examples that focus on percents. |
Percents |

|
Math Example--Percents--Percent Change--Example 9 | Math Example--Percents--Percent Change--Example 9
This is part of a collection of math examples that focus on percents. |
Percents |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1TopicRatios, Proportions, and Percents DescriptionThis example demonstrates how to solve a proportion problem where two ratios a:b and c:d are proportional. Given the values b = 3, c = 4, and d = 6, we need to find the value of a. The proportion is set up as a / 3 = 4 / 6, which is then solved to find that a = 2. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar triangles with algebraic expressions. Two triangles are shown, one with sides of 6 and 9, and the other with sides of 2x and 2x + 9. The problem requires setting up a proportion: 6 / 9 = 2x / (2x + 9). Solving this equation leads to x = 9, which then allows us to find the side lengths of 18 and 27. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, one with legs of 7 and 9, and the other with legs of 14 and x. The problem requires finding the length of side x by setting up a proportion based on the similar triangles: 7 / 9 = 14 / x. Solving this equation leads to x = 18. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, one with legs of 5 and 8, and the other with legs of 2x and (2x + 6). The problem requires setting up a proportion: 5 / 8 = 2x / (2x + 6). Solving this equation leads to x = 5, which then allows us to find the side lengths of 10 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°). Two triangles are shown, with the smaller one having sides of 6√3 and 6, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: (6√3) / 6 = x / 12. Solving this equation leads to x = 12√3. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°) and algebraic expressions. Two triangles are shown, with the smaller one having sides of 16 and 8, and the larger one having sides of (3x + 4) and 2x. The problem requires setting up a proportion: 16 / 8 = (3x + 4) / 2x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 8 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the smaller one having sides of 4 and 3, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: 4 / 3 = x / 12. Solving this equation leads to x = 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the smaller one having sides of (3x + 4) and 6, and the larger one having sides of 3x and 3x. The problem requires setting up a proportion: 8 / 6 = (3x + 4) / 3x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 12 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 12 / 5 = x / 15. Solving this equation leads to x = 36. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of 10x + 8 and 5x. The problem requires setting up a proportion: 12 / 5 = (10x + 8) / 5x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 20 and 48. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 19 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 19TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar isosceles right triangles. Two 45-45-90 triangles are shown, with one having sides labeled y and 5√2, and the other having sides labeled x and 12. The problem requires finding the lengths of both x and y using the special properties of isosceles right triangles and proportions. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 2 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 2TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion where b is expressed as x + 1, and c and d are given constants (c = 3, d = 2). The goal is to solve for a using the proportion a / b = c / d. By substituting the known values, we set up the equation a / (x + 1) = 3 / 2 and solve for a, resulting in the expression a = (3(x + 1)) / 2. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 20 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 20TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar isosceles right triangles with algebraic expressions. Two 45-45-90 triangles are shown, with one having sides labeled 15√2 and 15, and the other having sides labeled √2 * 5x and y. The problem requires finding the length of y in terms of x using the special properties of isosceles right triangles and proportions. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 21 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 21TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar isosceles triangles. Two isosceles triangles are shown, with the smaller one having sides of 30 and 16, and the larger one having sides of x and 20. The problem requires finding the length of side x by setting up a proportion: 30 / 16 = x / 20. Solving this equation leads to x = 37.5. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 22 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 22TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar isosceles triangles with algebraic expressions. Two isosceles triangles are shown, with the smaller one having sides of 22 and 12, and the larger one having sides of 10x + 5 and 6x. The problem requires setting up a proportion: 22 / 12 = (10x + 5) / 6x. Solving this equation leads to x = 5, which then allows us to find the side lengths of the larger triangle. |
Proportions |
|
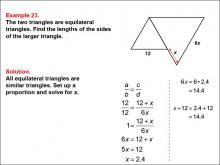
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 23 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 23TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar equilateral triangles. Two equilateral triangles are shown, with the smaller one having a side length of 12, and the larger one having a side length of 6x and an additional side labeled as 12 + x. The problem requires finding the lengths of the sides of the larger triangle by setting up a proportion: 12 / 12 = (12 + x) / 6x. Solving this equation leads to x = 2.4, and the length of the larger triangle's side is found to be approximately 14.4 units. |
Proportions |
|
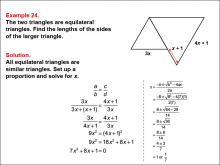
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 24 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 24TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a complex proportion problem using similar equilateral triangles with algebraic expressions. Two equilateral triangles are shown, with the smaller one having a side length of 3x, and the larger one having side lengths labeled as (4x + 1) and (x + 1). The problem requires setting up a proportion: 3x / (4x + 1) = 3x / (3x + (x + 1)). Solving this equation leads to a quadratic equation, which when solved gives x ≈ 7/1. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 25 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 25TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar rectangles. Two rectangles are shown, with the smaller one having sides of 2 and 3, and the larger one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 2 / 3 = x / 15. Solving this equation leads to x = 10. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 26 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 26TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar rectangles with algebraic expressions. Two rectangles are shown, with the smaller one having sides of 5 and 12, and the larger one having sides of x + 5 and 3x + 6. The problem requires setting up a proportion: 5 / 12 = (x + 5) / (3x + 6). Solving this equation leads to x = 10, which then allows us to find the side lengths of the larger rectangle as 15 and 36. |
Proportions |
|
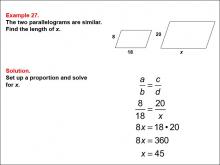
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 27 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 27TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar parallelograms. Two parallelograms are shown, with the smaller one having sides of 8 and 18, and the larger one having sides of 20 and x. The problem requires finding the length of side x by setting up a proportion: 8 / 18 = 20 / x. Solving this equation leads to x = 45. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 28 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 28TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar parallelograms with algebraic expressions. Two parallelograms are shown, with the smaller one having sides of 9 and 21, and the larger one having sides of x + 12 and 4x + 3. The problem requires setting up a proportion: 9 / 21 = (x + 12) / (4x + 3). Solving this equation leads to x = 15, which then allows us to find the side lengths of the larger parallelogram as 27 and 63. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 29 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 29TopicRatios, Proportions, and Percents DescriptionThis example demonstrates how to determine if two triangles are similar using proportions. Two triangles are shown, both with a 70° angle. The first triangle has sides of 12 and 10, while the second has sides of 18 and 15. The problem requires setting up a proportion to check for similarity: 12 / 10 = 18 / 15. After simplifying, both ratios are equal (6 / 5 = 6 / 5), confirming that the triangles are indeed similar. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 3 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 3TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving for b in a proportion where a = 8, c = 4, and d = 3. We set up the proportion 8 / b = 4 / 3 and solve for b, resulting in b = 6. This problem shows how to find an unknown value in the denominator of a proportion. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 30 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 30TopicRatios, Proportions, and Percents DescriptionThis example illustrates how to determine if two triangles are not similar using proportions. Two triangles are shown, both with a 75° angle. The first triangle has sides of 15 and 9, while the second has sides of 28 and 18. The problem requires setting up a proportion to check for similarity: 15 / 9 = 28 / 18. After simplifying, the ratios are not equal (5 / 3 ≠ 14 / 9), concluding that the triangles are not similar. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 31 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 31TopicRatios, Proportions, and Percents DescriptionThis example demonstrates how to determine if two right triangles are similar using proportions. Two right triangles are shown, one with legs of length 4 and 3, and the other with legs of length 10 and 7.5. The problem requires setting up a proportion to check for similarity: 4 / 3 = 10 / 7.5. After simplifying, both ratios are equal (4 / 3 = 4 / 3), confirming that the triangles are indeed similar. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 32 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 32TopicRatios, Proportions, and Percents DescriptionThis example illustrates how to determine if two right triangles are not similar using proportions. Two right triangles are shown, one with legs of length 12 and 5, and the other with legs of length 35 and 15. The problem requires setting up a proportion to check for similarity: 12 / 5 = 35 / 15. After simplifying, the ratios are not equal (12 / 5 ≠ 7 / 3), concluding that the triangles are not similar. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 33 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 33TopicRatios, Proportions, and Percents DescriptionThis example demonstrates how to determine if two rectangles are similar using proportions. Two rectangles are shown, with the first having dimensions 3 and 8, and the second having dimensions 9 and 24. The problem requires setting up a proportion to check for similarity: 3 / 8 = 9 / 24. After simplifying, the ratios are equal, confirming that the rectangles are indeed similar. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 34 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 34TopicRatios, Proportions, and Percents DescriptionThis example illustrates how to determine if two rectangles are similar using proportions with algebraic expressions. Two rectangles are shown, with the first having dimensions 11.5 and 23, and the second having dimensions 23x and 46x. The problem requires setting up a proportion to check for similarity: 11.5 / 23 = 23x / 46x. After simplifying, the ratios are equal, confirming that the rectangles are indeed similar for any value of x. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 35 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 35TopicRatios, Proportions, and Percents DescriptionThis example demonstrates how to determine if two parallelograms are similar using proportions. Two parallelograms are shown, with the first having dimensions 6 and 9, and the second having dimensions 15 and 22.5. The problem requires setting up a proportion to check for similarity: 6 / 9 = 15 / 22.5. After simplifying, the ratios are equal, confirming that the parallelograms are indeed similar. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 36 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 36TopicRatios, Proportions, and Percents DescriptionThis example demonstrates how to determine if two parallelograms are not similar using proportions. Two parallelograms are shown, with the first having dimensions 9 and 28, and the second having dimensions 18 and 54. The problem requires setting up a proportion to check for similarity: 9 / 18 ≠ 28 / 54. After simplifying, the ratios are not equal, concluding that the parallelograms are not similar. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 37 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 37TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar triangles with algebraic expressions. Two triangles are shown, one with side lengths 9 and 18, and the other with expressions 6x and 10x + 6. The problem requires setting up a proportion to determine the value of x for which the triangles are similar: 9 / 18 = 6x / (10x + 6). Solving this equation leads to x = 3. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 38 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 38TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, one with side lengths 4 and 3, and the other with expressions 3x and 2x + 1. The problem requires setting up a proportion to determine the value of x for which the triangles are similar: 4 / 3 = 3x / (2x + 1). Solving this equation leads to x = 4. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 39 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 39TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar rectangles with an unknown side length. Two rectangles are shown, one with side lengths of 4 and x, and the other with side lengths of 15 and 4. The problem requires setting up a proportion to determine the value of x for which the rectangles are similar: 4 / 15 = x / 4. Solving this equation leads to x = 16/15. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 4 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 4TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving for b in a proportion where a is expressed as x + 2, and c and d are given constants (c = 5, d = 2). We set up the equation (x + 2) / b = 5 / 2 and solve for b, resulting in the expression b = (2(x + 2)) / 5. This problem demonstrates how to handle algebraic expressions in proportions. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 40 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 40TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar parallelograms with algebraic expressions. Two parallelograms are shown, one with side lengths of 6 and x, and the other with expressions of 3x + 2 and 22. The problem requires setting up a proportion to determine the value of x for which the parallelograms are similar: 6 / 22 = x / (3x + 2). Solving this equation leads to x = 3. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 5 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 5TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving for c in a proportion where a = 9, b = 4, and d = 12. We set up the proportion 9 / 4 = c / 12 and solve for c, resulting in c = 27. This problem shows how to find an unknown value in the numerator of a proportion. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 6 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 6TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving for c in a proportion where a = 8, b = 3, and d is expressed as x + 3. We set up the equation 8 / 3 = c / (x + 3) and solve for c, resulting in the expression c = (8(x + 3)) / 3. This problem demonstrates how to handle algebraic expressions in the denominator of a proportion. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 7 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 7TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving for d in a proportion where a = 12, b = 5, and c = 48. We set up the proportion 12 / 5 = 48 / d and solve for d, resulting in d = 20. This problem shows how to find an unknown value in the denominator of a proportion when all other values are known. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 8 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 8TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving for d in a proportion where a = 11, b = 5, and c is expressed as x - 4. We set up the equation 11 / 5 = (x - 4) / d and solve for d, resulting in the expression d = (5(x - 4)) / 11. This problem demonstrates how to handle algebraic expressions in the numerator of a proportion. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 9 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 9TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar triangles. Two triangles are shown, with one having sides of 3 and 4, and the other having sides of 6 and x. The problem requires finding the length of side x by setting up a proportion based on the similar triangles: 3 / 4 = 6 / x. Solving this equation leads to x = 8. |
Proportions |
|
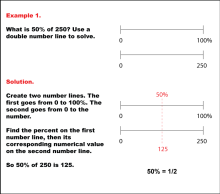
Math Example: Percents with Double Number Lines: Example 1 | Math Example: Percents with Double Number Lines: Example 1TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to find 50% of 250 using a double number line. The solution shows two parallel number lines: one ranging from 0 to 100% and the other from 0 to 250. By aligning 50% on the percentage line with its corresponding value on the numerical line, we can see that 50% of 250 is 125. This method visually represents the concept that 50% is equivalent to one-half of a quantity. |
Ratios and Rates |
|
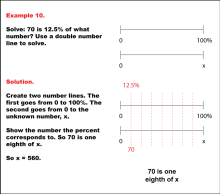
Math Example: Percents with Double Number Lines: Example 10 | Math Example: Percents with Double Number Lines: Example 10TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine an unknown value using a double number line when given a part and its corresponding percentage, involving a decimal percentage. The image shows two number lines: one ranging from 0 to 100% and another from 0 to an unknown number x. The position 70 is marked on the second line, visually illustrating the process of finding x when 70 is 12.5% of x. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 11 | Math Example: Percents with Double Number Lines: Example 11TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine what percent one number is of another using a double number line. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to 75, with 25 marked as an intermediate point. This visual representation helps students understand the relationship between the part (25) and the whole (75) in percentage terms. |
Ratios and Rates |
|
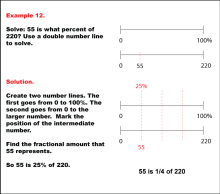
Math Example: Percents with Double Number Lines: Example 12 | Math Example: Percents with Double Number Lines: Example 12TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate what percent one number is of another using a double number line. The image depicts two parallel number lines: one spanning from 0 to 100% and another from 0 to 220, with 55 marked as an intermediate point. This visual representation helps students understand the relationship between the part (55) and the whole (220) in percentage terms. |
Ratios and Rates |
|
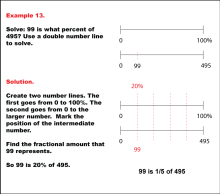
Math Example: Percents with Double Number Lines: Example 13 | Math Example: Percents with Double Number Lines: Example 13TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine what percent one number is of another using a double number line. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to 495, with 99 marked as an intermediate point. This visual representation helps students understand the relationship between the part (99) and the whole (495) in percentage terms. |
Ratios and Rates |

|
Math Example: Percents with Double Number Lines: Example 14 | Math Example: Percents with Double Number Lines: Example 14TopicRatios, Proportions, Percents DescriptionThis example illustrates how to calculate what percent one number is of another using a double number line. The image depicts two parallel number lines: one spanning from 0 to 100% and another from 0 to 396, with 198 marked at the midpoint. This visual representation helps students understand the relationship between the part (198) and the whole (396) in percentage terms. |
Ratios and Rates |
|
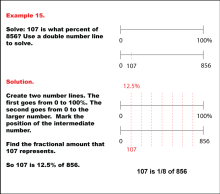
Math Example: Percents with Double Number Lines: Example 15 | Math Example: Percents with Double Number Lines: Example 15TopicRatios, Proportions, Percents DescriptionThis example demonstrates how to determine what percent one number is of another using a double number line, particularly when dealing with more complex ratios. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to 856, with 107 marked at an eighth of the way. This visual representation helps students understand the relationship between the part (107) and the whole (856) in percentage terms. |
Ratios and Rates |