Illustrative Math Alignment: Grade 6 Unit 1
Dividing Fractions
Lesson 8: How Much in Each Group? (Part 1)
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
Math Example: Fraction Operations--Dividing Fractions: Example 8 | Dividing Fractions: Example 8TopicFraction Operations DescriptionThis example demonstrates the division of fractions by illustrating the conversion of the division operation into multiplication by the reciprocal. The image serves as a guide to understanding the method of flipping the second fraction and multiplying, showcasing the concept of reciprocal multiplication. Key skills include identifying reciprocal relationships, multiplying fractions, and simplifying results. This example is instrumental in helping students understand the mechanics of dividing fractions, which is a pivotal skill in mastering fraction operations. |
Fractions and Mixed Numbers |
|
Math Example: Fraction Operations--Dividing Fractions: Example 9 | Dividing Fractions: Example 9TopicFraction Operations DescriptionThis example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. In this example the quotient equals 1. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 9 | Dividing Fractions: Example 9TopicFraction Operations DescriptionThis example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. In this example the quotient equals 1. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 9 | Dividing Fractions: Example 9TopicFraction Operations DescriptionThis example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. In this example the quotient equals 1. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 9 | Dividing Fractions: Example 9TopicFraction Operations DescriptionThis example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. In this example the quotient equals 1. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 9 | Dividing Fractions: Example 9TopicFraction Operations DescriptionThis example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. In this example the quotient equals 1. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic. |
Fractions and Mixed Numbers |
|
Math Example: Fraction Operations--Dividing Fractions: Example 10 | Dividing Fractions: Example 10TopicFraction Operations DescriptionThis example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. In this example the result is a mixed number. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 10 | Dividing Fractions: Example 10TopicFraction Operations DescriptionThis example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. In this example the result is a mixed number. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 10 | Dividing Fractions: Example 10TopicFraction Operations DescriptionThis example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. In this example the result is a mixed number. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 10 | Dividing Fractions: Example 10TopicFraction Operations DescriptionThis example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. In this example the result is a mixed number. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 10 | Dividing Fractions: Example 10TopicFraction Operations DescriptionThis example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. In this example the result is a mixed number. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations. |
Fractions and Mixed Numbers |
|
Math Example: Fraction Operations--Dividing Fractions: Example 11 | Dividing Fractions: Example 11TopicFraction Operations DescriptionThis example demonstrates the division of fractions by illustrating the conversion of division into multiplication using the reciprocal of the divisor. The visual guide helps learners understand the transformation and the subsequent multiplication process. In this example, the result is a mixed number. Key skills include identifying reciprocal relationships, executing multiplication, and simplifying fractions. This example is instrumental in building a solid understanding of how dividing fractions simplifies into a multiplication problem, enhancing students' problem-solving skills in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 11 | Dividing Fractions: Example 11TopicFraction Operations DescriptionThis example demonstrates the division of fractions by illustrating the conversion of division into multiplication using the reciprocal of the divisor. The visual guide helps learners understand the transformation and the subsequent multiplication process. In this example, the result is a mixed number. Key skills include identifying reciprocal relationships, executing multiplication, and simplifying fractions. This example is instrumental in building a solid understanding of how dividing fractions simplifies into a multiplication problem, enhancing students' problem-solving skills in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 11 | Dividing Fractions: Example 11TopicFraction Operations DescriptionThis example demonstrates the division of fractions by illustrating the conversion of division into multiplication using the reciprocal of the divisor. The visual guide helps learners understand the transformation and the subsequent multiplication process. In this example, the result is a mixed number. Key skills include identifying reciprocal relationships, executing multiplication, and simplifying fractions. This example is instrumental in building a solid understanding of how dividing fractions simplifies into a multiplication problem, enhancing students' problem-solving skills in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 11 | Dividing Fractions: Example 11TopicFraction Operations DescriptionThis example demonstrates the division of fractions by illustrating the conversion of division into multiplication using the reciprocal of the divisor. The visual guide helps learners understand the transformation and the subsequent multiplication process. In this example, the result is a mixed number. Key skills include identifying reciprocal relationships, executing multiplication, and simplifying fractions. This example is instrumental in building a solid understanding of how dividing fractions simplifies into a multiplication problem, enhancing students' problem-solving skills in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 11 | Dividing Fractions: Example 11TopicFraction Operations DescriptionThis example demonstrates the division of fractions by illustrating the conversion of division into multiplication using the reciprocal of the divisor. The visual guide helps learners understand the transformation and the subsequent multiplication process. In this example, the result is a mixed number. Key skills include identifying reciprocal relationships, executing multiplication, and simplifying fractions. This example is instrumental in building a solid understanding of how dividing fractions simplifies into a multiplication problem, enhancing students' problem-solving skills in fraction arithmetic. |
Fractions and Mixed Numbers |
|
Math Example: Fraction Operations--Dividing Fractions: Example 12 | Dividing Fractions: Example 12TopicFraction Operations DescriptionThis example focuses on dividing fractions by converting the division into multiplication using the reciprocal of the divisor. The image visually represents the process, emphasizing the importance of understanding reciprocal operations. In this example the result is a mixed number. Skills involved include recognizing equivalent fractions, performing multiplication, and simplifying fractions to their lowest terms. This example is crucial for students to grasp how division of fractions simplifies into a multiplication problem, enhancing their problem-solving capabilities in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 12 | Dividing Fractions: Example 12TopicFraction Operations DescriptionThis example focuses on dividing fractions by converting the division into multiplication using the reciprocal of the divisor. The image visually represents the process, emphasizing the importance of understanding reciprocal operations. In this example the result is a mixed number. Skills involved include recognizing equivalent fractions, performing multiplication, and simplifying fractions to their lowest terms. This example is crucial for students to grasp how division of fractions simplifies into a multiplication problem, enhancing their problem-solving capabilities in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 12 | Dividing Fractions: Example 12TopicFraction Operations DescriptionThis example focuses on dividing fractions by converting the division into multiplication using the reciprocal of the divisor. The image visually represents the process, emphasizing the importance of understanding reciprocal operations. In this example the result is a mixed number. Skills involved include recognizing equivalent fractions, performing multiplication, and simplifying fractions to their lowest terms. This example is crucial for students to grasp how division of fractions simplifies into a multiplication problem, enhancing their problem-solving capabilities in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 12 | Dividing Fractions: Example 12TopicFraction Operations DescriptionThis example focuses on dividing fractions by converting the division into multiplication using the reciprocal of the divisor. The image visually represents the process, emphasizing the importance of understanding reciprocal operations. In this example the result is a mixed number. Skills involved include recognizing equivalent fractions, performing multiplication, and simplifying fractions to their lowest terms. This example is crucial for students to grasp how division of fractions simplifies into a multiplication problem, enhancing their problem-solving capabilities in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 12 | Dividing Fractions: Example 12TopicFraction Operations DescriptionThis example focuses on dividing fractions by converting the division into multiplication using the reciprocal of the divisor. The image visually represents the process, emphasizing the importance of understanding reciprocal operations. In this example the result is a mixed number. Skills involved include recognizing equivalent fractions, performing multiplication, and simplifying fractions to their lowest terms. This example is crucial for students to grasp how division of fractions simplifies into a multiplication problem, enhancing their problem-solving capabilities in fraction arithmetic. |
Fractions and Mixed Numbers |
|
Math Example: Fraction Operations--Dividing Fractions: Example 13 | Dividing Fractions: Example 13TopicFraction Operations DescriptionThis example demonstrates the division of fractions by illustrating the conversion of the division operation into multiplication by the reciprocal. The image serves as a guide to understanding the method of flipping the second fraction and multiplying, showcasing the concept of reciprocal multiplication. The result is a mixed number. Key skills include identifying reciprocal relationships, multiplying fractions, and simplifying results. This example is instrumental in helping students understand the mechanics of dividing fractions, which is a pivotal skill in mastering fraction operations. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 13 | Dividing Fractions: Example 13TopicFraction Operations DescriptionThis example demonstrates the division of fractions by illustrating the conversion of the division operation into multiplication by the reciprocal. The image serves as a guide to understanding the method of flipping the second fraction and multiplying, showcasing the concept of reciprocal multiplication. The result is a mixed number. Key skills include identifying reciprocal relationships, multiplying fractions, and simplifying results. This example is instrumental in helping students understand the mechanics of dividing fractions, which is a pivotal skill in mastering fraction operations. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 13 | Dividing Fractions: Example 13TopicFraction Operations DescriptionThis example demonstrates the division of fractions by illustrating the conversion of the division operation into multiplication by the reciprocal. The image serves as a guide to understanding the method of flipping the second fraction and multiplying, showcasing the concept of reciprocal multiplication. The result is a mixed number. Key skills include identifying reciprocal relationships, multiplying fractions, and simplifying results. This example is instrumental in helping students understand the mechanics of dividing fractions, which is a pivotal skill in mastering fraction operations. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 13 | Dividing Fractions: Example 13TopicFraction Operations DescriptionThis example demonstrates the division of fractions by illustrating the conversion of the division operation into multiplication by the reciprocal. The image serves as a guide to understanding the method of flipping the second fraction and multiplying, showcasing the concept of reciprocal multiplication. The result is a mixed number. Key skills include identifying reciprocal relationships, multiplying fractions, and simplifying results. This example is instrumental in helping students understand the mechanics of dividing fractions, which is a pivotal skill in mastering fraction operations. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 13 | Dividing Fractions: Example 13TopicFraction Operations DescriptionThis example demonstrates the division of fractions by illustrating the conversion of the division operation into multiplication by the reciprocal. The image serves as a guide to understanding the method of flipping the second fraction and multiplying, showcasing the concept of reciprocal multiplication. The result is a mixed number. Key skills include identifying reciprocal relationships, multiplying fractions, and simplifying results. This example is instrumental in helping students understand the mechanics of dividing fractions, which is a pivotal skill in mastering fraction operations. |
Fractions and Mixed Numbers |
|
Math Example: Fraction Operations--Dividing Fractions: Example 14 | Dividing Fractions: Example 14TopicFraction Operations DescriptionThis example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. The result is a mixed number. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 14 | Dividing Fractions: Example 14TopicFraction Operations DescriptionThis example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. The result is a mixed number. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 14 | Dividing Fractions: Example 14TopicFraction Operations DescriptionThis example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. The result is a mixed number. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 14 | Dividing Fractions: Example 14TopicFraction Operations DescriptionThis example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. The result is a mixed number. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 14 | Dividing Fractions: Example 14TopicFraction Operations DescriptionThis example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. The result is a mixed number. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic. |
Fractions and Mixed Numbers |
|
Math Example: Fraction Operations--Dividing Fractions: Example 15 | Dividing Fractions: Example 15TopicFraction Operations DescriptionThis example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. The result is a mixed number. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 15 | Dividing Fractions: Example 15TopicFraction Operations DescriptionThis example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. The result is a mixed number. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 15 | Dividing Fractions: Example 15TopicFraction Operations DescriptionThis example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. The result is a mixed number. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 15 | Dividing Fractions: Example 15TopicFraction Operations DescriptionThis example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. The result is a mixed number. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations. |
Fractions and Mixed Numbers |
|
|
Math Example: Fraction Operations--Dividing Fractions: Example 15 | Dividing Fractions: Example 15TopicFraction Operations DescriptionThis example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. The result is a mixed number. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations. |
Fractions and Mixed Numbers |
|
Math Clip Art--Fraction Concepts--Circular Fraction Model, Halves | Math Clip Art--Fraction Concepts--Circular Fraction Model, HalvesTopicFractions DescriptionThe circular fraction model for halves is a fundamental visual aid in teaching the concept of fractions, specifically halves. This math clip art image showcases a circle divided into two equal segments, each representing one-half of the whole. The clear, distinct division makes it exceptionally easy for students to visualize and understand the concept of parts of a whole in relation to halves. |
Identify and Name Fractions |
|
|
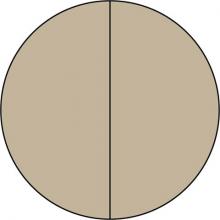
Math Clip Art--Fraction Concepts--Circular Fraction Model, Halves | Math Clip Art--Fraction Concepts--Circular Fraction Model, HalvesTopicFractions DescriptionThe circular fraction model for halves is a fundamental visual aid in teaching the concept of fractions, specifically halves. This math clip art image showcases a circle divided into two equal segments, each representing one-half of the whole. The clear, distinct division makes it exceptionally easy for students to visualize and understand the concept of parts of a whole in relation to halves. |
Identify and Name Fractions |
|
|
Math Clip Art--Fraction Concepts--Circular Fraction Model, Halves | Math Clip Art--Fraction Concepts--Circular Fraction Model, HalvesTopicFractions DescriptionThe circular fraction model for halves is a fundamental visual aid in teaching the concept of fractions, specifically halves. This math clip art image showcases a circle divided into two equal segments, each representing one-half of the whole. The clear, distinct division makes it exceptionally easy for students to visualize and understand the concept of parts of a whole in relation to halves. |
Identify and Name Fractions |
|
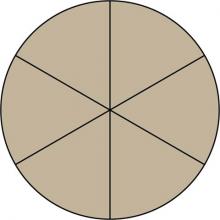
Math Clip Art--Fraction Concepts--Circular Fraction Model, Sixths | Math Clip Art--Fraction Concepts--Circular Fraction Model, SixthsTopicFractions DescriptionThe circular fraction model for sixths is an important visual aid in teaching the concept of fractions, specifically sixths. This math clip art image presents a circle divided into six equal segments, each representing one-sixth of the whole. The clear, distinct divisions make it easy for students to visualize and comprehend the concept of parts of a whole in relation to sixths. |
Identify and Name Fractions |
|
|
Math Clip Art--Fraction Concepts--Circular Fraction Model, Sixths | Math Clip Art--Fraction Concepts--Circular Fraction Model, SixthsTopicFractions DescriptionThe circular fraction model for sixths is an important visual aid in teaching the concept of fractions, specifically sixths. This math clip art image presents a circle divided into six equal segments, each representing one-sixth of the whole. The clear, distinct divisions make it easy for students to visualize and comprehend the concept of parts of a whole in relation to sixths. |
Identify and Name Fractions |
|
|
Math Clip Art--Fraction Concepts--Circular Fraction Model, Sixths | Math Clip Art--Fraction Concepts--Circular Fraction Model, SixthsTopicFractions DescriptionThe circular fraction model for sixths is an important visual aid in teaching the concept of fractions, specifically sixths. This math clip art image presents a circle divided into six equal segments, each representing one-sixth of the whole. The clear, distinct divisions make it easy for students to visualize and comprehend the concept of parts of a whole in relation to sixths. |
Identify and Name Fractions |
|
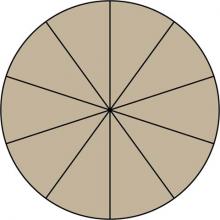
Math Clip Art--Fraction Concepts--Circular Fraction Model, Tenths | Math Clip Art--Fraction Concepts--Circular Fraction Model, TenthsTopicFractions DescriptionThe circular fraction model for tenths is a valuable visual aid in teaching the concept of fractions, specifically tenths. This math clip art image displays a circle divided into ten equal segments, each representing one-tenth of the whole. The clear, distinct divisions make it easy for students to visualize and understand the concept of parts of a whole in relation to tenths. |
Identify and Name Fractions |
|
|
Math Clip Art--Fraction Concepts--Circular Fraction Model, Tenths | Math Clip Art--Fraction Concepts--Circular Fraction Model, TenthsTopicFractions DescriptionThe circular fraction model for tenths is a valuable visual aid in teaching the concept of fractions, specifically tenths. This math clip art image displays a circle divided into ten equal segments, each representing one-tenth of the whole. The clear, distinct divisions make it easy for students to visualize and understand the concept of parts of a whole in relation to tenths. |
Identify and Name Fractions |
|
|
Math Clip Art--Fraction Concepts--Circular Fraction Model, Tenths | Math Clip Art--Fraction Concepts--Circular Fraction Model, TenthsTopicFractions DescriptionThe circular fraction model for tenths is a valuable visual aid in teaching the concept of fractions, specifically tenths. This math clip art image displays a circle divided into ten equal segments, each representing one-tenth of the whole. The clear, distinct divisions make it easy for students to visualize and understand the concept of parts of a whole in relation to tenths. |
Identify and Name Fractions |
|
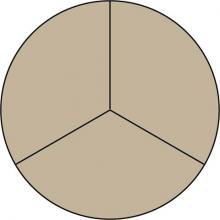
Math Clip Art--Fraction Concepts--Circular Fraction Model, Thirds | Math Clip Art--Fraction Concepts--Circular Fraction Model, ThirdsTopicFractions DescriptionThe circular fraction model for thirds is an essential visual representation used in teaching fractions, specifically the concept of thirds. The clip art image presents a circle divided into three equal segments, each segment representing one-third of the whole. This clear division allows students to visualize how a whole can be split into equal parts. |
Identify and Name Fractions |
|
|
Math Clip Art--Fraction Concepts--Circular Fraction Model, Thirds | Math Clip Art--Fraction Concepts--Circular Fraction Model, ThirdsTopicFractions DescriptionThe circular fraction model for thirds is an essential visual representation used in teaching fractions, specifically the concept of thirds. The clip art image presents a circle divided into three equal segments, each segment representing one-third of the whole. This clear division allows students to visualize how a whole can be split into equal parts. |
Identify and Name Fractions |
|
|
Math Clip Art--Fraction Concepts--Circular Fraction Model, Thirds | Math Clip Art--Fraction Concepts--Circular Fraction Model, ThirdsTopicFractions DescriptionThe circular fraction model for thirds is an essential visual representation used in teaching fractions, specifically the concept of thirds. The clip art image presents a circle divided into three equal segments, each segment representing one-third of the whole. This clear division allows students to visualize how a whole can be split into equal parts. |
Identify and Name Fractions |
|
Math Clip Art--Fraction Concepts--Fraction Bars, Fourths | Math Clip Art--Fraction Concepts--Fraction Bars, FourthsTopicFractions DescriptionThe fraction bar model for fourths is a powerful visual tool for teaching the concept of fractions, specifically quarters or fourths. This math clip art image presents a rectangular bar divided into four equal segments, each representing one-fourth of the whole. The clear, linear divisions make it easy for students to visualize and comprehend the concept of parts of a whole in relation to fourths. |
Fractions and Mixed Numbers |
|
|
Math Clip Art--Fraction Concepts--Fraction Bars, Fourths | Math Clip Art--Fraction Concepts--Fraction Bars, FourthsTopicFractions DescriptionThe fraction bar model for fourths is a powerful visual tool for teaching the concept of fractions, specifically quarters or fourths. This math clip art image presents a rectangular bar divided into four equal segments, each representing one-fourth of the whole. The clear, linear divisions make it easy for students to visualize and comprehend the concept of parts of a whole in relation to fourths. |
Fractions and Mixed Numbers |
