
Illustrative Math Alignment: Grade 6 Unit 1
Arithmetic in Base Ten
Lesson 6: Methods for Multiplying Decimals
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail | Title | Description | Curriculum Nodes |
|---|---|---|---|

|
Definition--Closure Property Topics--Whole Numbers and Closure: Division | Whole Numbers and Closure: DivisionTopicMath Properties DefinitionThe set of whole numbers is not closed under division, meaning that the quotient of two whole numbers is not always a whole number. DescriptionThe concept of closure for whole numbers under division is an important property in mathematics. It demonstrates that while whole numbers have many interesting properties, they do not form a closed system under division. This property helps students understand the relationships between whole numbers and introduces them to the concept of rational numbers. |
Numerical Expressions |

|
Definition--Closure Property Topics--Whole Numbers and Closure: Multiplication | Whole Numbers and Closure: MultiplicationTopicMath Properties DefinitionThe closure property for multiplication of whole numbers states that the product of any two whole numbers is always another whole number. DescriptionThe closure property for multiplication of whole numbers is a fundamental concept in mathematics that demonstrates the consistency and completeness of the whole number system. This property ensures that when we multiply any two whole numbers, the result is always another whole number, keeping us within the same number system. |
Numerical Expressions |

|
Definition--Closure Property Topics--Whole Numbers and Closure: Subtraction | Whole Numbers and Closure: SubtractionTopicMath Properties DefinitionThe set of whole numbers is not closed under subtraction, meaning that the difference between two whole numbers is not always a whole number. DescriptionThe concept of closure for whole numbers under subtraction is an important property in mathematics. It demonstrates that while whole numbers have many interesting properties, they do not form a closed system under subtraction. This property helps students understand the relationships between whole numbers and introduces them to the concept of integers. |
Numerical Expressions |

|
Definition--Common Factor | Definition--Common Factor
This is part of a collection of math definitions from Media4Math's Visual Glossary. |
Numerical Expressions and Variable Expressions |

|
Definition--Common Factor | Definition--Common Factor
This is part of a collection of math definitions from Media4Math's Visual Glossary. |
Numerical Expressions and Variable Expressions |

|
Definition--Complex Conjugate | Definition--Complex Conjugate
This is part of a collection of math definitions from Media4Math's Visual Glossary. |
Numerical Expressions and Variable Expressions |

|
Definition--Complex Conjugate | Definition--Complex Conjugate
This is part of a collection of math definitions from Media4Math's Visual Glossary. |
Numerical Expressions and Variable Expressions |

|
Definition--Complex Number | Definition--Complex Number
This is part of a collection of math definitions from Media4Math's Visual Glossary. |
Numerical Expressions and Variable Expressions |

|
Definition--Complex Number | Definition--Complex Number
This is part of a collection of math definitions from Media4Math's Visual Glossary. |
Numerical Expressions and Variable Expressions |

|
Definition--Conjugate | Definition--Conjugate
This is part of a collection of math definitions from Media4Math's Visual Glossary. |
Numerical Expressions and Variable Expressions |

|
Definition--Conjugate | Definition--Conjugate
This is part of a collection of math definitions from Media4Math's Visual Glossary. |
Numerical Expressions and Variable Expressions |

|
Definition--Equation Concepts--Numerical Expression | Numerical ExpressionTopicEquations DefinitionA numerical expression is a mathematical phrase involving numbers and operation symbols, but no variables. DescriptionNumerical expressions consist of numbers and operations such as addition, subtraction, multiplication, and division. For example, 3 + 4 × 2 is a numerical expression. These expressions are evaluated to find their value. In real-world applications, numerical expressions are used in everyday calculations such as budgeting, measuring, and data analysis. Understanding numerical expressions helps students perform arithmetic operations and develop computational skills. |
Numerical Expressions |

|
Definition--Equation Concepts--Numerical Expression | Numerical ExpressionTopicEquations DefinitionA numerical expression is a mathematical phrase involving numbers and operation symbols, but no variables. DescriptionNumerical expressions consist of numbers and operations such as addition, subtraction, multiplication, and division. For example, 3 + 4 × 2 is a numerical expression. These expressions are evaluated to find their value. In real-world applications, numerical expressions are used in everyday calculations such as budgeting, measuring, and data analysis. Understanding numerical expressions helps students perform arithmetic operations and develop computational skills. |
Numerical Expressions |

|
Definition--Equation Concepts--Numerical Expression | Numerical ExpressionTopicEquations DefinitionA numerical expression is a mathematical phrase involving numbers and operation symbols, but no variables. DescriptionNumerical expressions consist of numbers and operations such as addition, subtraction, multiplication, and division. For example, 3 + 4 × 2 is a numerical expression. These expressions are evaluated to find their value. In real-world applications, numerical expressions are used in everyday calculations such as budgeting, measuring, and data analysis. Understanding numerical expressions helps students perform arithmetic operations and develop computational skills. |
Numerical Expressions |

|
Definition--Equation Concepts--Numerical Expression | Numerical ExpressionTopicEquations DefinitionA numerical expression is a mathematical phrase involving numbers and operation symbols, but no variables. DescriptionNumerical expressions consist of numbers and operations such as addition, subtraction, multiplication, and division. For example, 3 + 4 × 2 is a numerical expression. These expressions are evaluated to find their value. In real-world applications, numerical expressions are used in everyday calculations such as budgeting, measuring, and data analysis. Understanding numerical expressions helps students perform arithmetic operations and develop computational skills. |
Numerical Expressions |
|
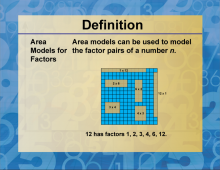
Definition--Factors and Multiples--Area Models for Factors | Area Models for FactorsTopicFactors and Multiples DefinitionFactors are numbers that divide another number without leaving a remainder, while multiples are the result of multiplying a number by an integer. DescriptionUnderstanding factors and multiples is crucial in mathematics, particularly in number theory and algebra. Factors are the building blocks of numbers, representing the integers that can be multiplied together to produce another number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Multiples, on the other hand, are the product of a number and any integer. For instance, the multiples of 5 include 5, 10, 15, 20, and so on. |
Numerical Expressions |

|
Definition--Factors and Multiples--Area Models for Factors | Area Models for FactorsTopicFactors and Multiples DefinitionFactors are numbers that divide another number without leaving a remainder, while multiples are the result of multiplying a number by an integer. DescriptionUnderstanding factors and multiples is crucial in mathematics, particularly in number theory and algebra. Factors are the building blocks of numbers, representing the integers that can be multiplied together to produce another number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Multiples, on the other hand, are the product of a number and any integer. For instance, the multiples of 5 include 5, 10, 15, 20, and so on. |
Numerical Expressions |

|
Definition--Factors and Multiples--Area Models for Factors | Area Models for FactorsTopicFactors and Multiples DefinitionFactors are numbers that divide another number without leaving a remainder, while multiples are the result of multiplying a number by an integer. DescriptionUnderstanding factors and multiples is crucial in mathematics, particularly in number theory and algebra. Factors are the building blocks of numbers, representing the integers that can be multiplied together to produce another number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Multiples, on the other hand, are the product of a number and any integer. For instance, the multiples of 5 include 5, 10, 15, 20, and so on. |
Numerical Expressions |

|
Definition--Factors and Multiples--Area Models for Factors | Area Models for FactorsTopicFactors and Multiples DefinitionFactors are numbers that divide another number without leaving a remainder, while multiples are the result of multiplying a number by an integer. DescriptionUnderstanding factors and multiples is crucial in mathematics, particularly in number theory and algebra. Factors are the building blocks of numbers, representing the integers that can be multiplied together to produce another number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Multiples, on the other hand, are the product of a number and any integer. For instance, the multiples of 5 include 5, 10, 15, 20, and so on. |
Numerical Expressions |

|
Definition--Factors and Multiples--Area Models for Factors | Area Models for FactorsTopicFactors and Multiples DefinitionFactors are numbers that divide another number without leaving a remainder, while multiples are the result of multiplying a number by an integer. DescriptionUnderstanding factors and multiples is crucial in mathematics, particularly in number theory and algebra. Factors are the building blocks of numbers, representing the integers that can be multiplied together to produce another number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Multiples, on the other hand, are the product of a number and any integer. For instance, the multiples of 5 include 5, 10, 15, 20, and so on. |
Numerical Expressions |

|
Definition--Factors and Multiples--Common Factors | Common FactorsTopicFactors and Multiples DefinitionA common factor is a number that divides two or more numbers exactly without leaving a remainder. DescriptionCommon factors are integral to understanding the mathematical concepts of factors and multiples. They are the numbers that can divide two or more given numbers without leaving a remainder. For example, if you consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. This is because these numbers can divide both 12 and 18 exactly, with no remainder. |
Numerical Expressions |

|
Definition--Factors and Multiples--Common Factors | Common FactorsTopicFactors and Multiples DefinitionA common factor is a number that divides two or more numbers exactly without leaving a remainder. DescriptionCommon factors are integral to understanding the mathematical concepts of factors and multiples. They are the numbers that can divide two or more given numbers without leaving a remainder. For example, if you consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. This is because these numbers can divide both 12 and 18 exactly, with no remainder. |
Numerical Expressions |

|
Definition--Factors and Multiples--Common Factors | Common FactorsTopicFactors and Multiples DefinitionA common factor is a number that divides two or more numbers exactly without leaving a remainder. DescriptionCommon factors are integral to understanding the mathematical concepts of factors and multiples. They are the numbers that can divide two or more given numbers without leaving a remainder. For example, if you consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. This is because these numbers can divide both 12 and 18 exactly, with no remainder. |
Numerical Expressions |

|
Definition--Factors and Multiples--Common Factors | Common FactorsTopicFactors and Multiples DefinitionA common factor is a number that divides two or more numbers exactly without leaving a remainder. DescriptionCommon factors are integral to understanding the mathematical concepts of factors and multiples. They are the numbers that can divide two or more given numbers without leaving a remainder. For example, if you consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. This is because these numbers can divide both 12 and 18 exactly, with no remainder. |
Numerical Expressions |

|
Definition--Factors and Multiples--Common Factors | Common FactorsTopicFactors and Multiples DefinitionA common factor is a number that divides two or more numbers exactly without leaving a remainder. DescriptionCommon factors are integral to understanding the mathematical concepts of factors and multiples. They are the numbers that can divide two or more given numbers without leaving a remainder. For example, if you consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. This is because these numbers can divide both 12 and 18 exactly, with no remainder. |
Numerical Expressions |

|
Definition--Factors and Multiples--Common Factors | Common FactorsTopicFactors and Multiples DefinitionA common factor is a number that divides two or more numbers exactly without leaving a remainder. DescriptionCommon factors are integral to understanding the mathematical concepts of factors and multiples. They are the numbers that can divide two or more given numbers without leaving a remainder. For example, if you consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. This is because these numbers can divide both 12 and 18 exactly, with no remainder. |
Numerical Expressions |

|
Definition--Factors and Multiples--Common Multiples | Common MultiplesTopicFactors and Multiples DefinitionA common multiple is a number that is a multiple of two or more numbers. DescriptionIn the context of factors and multiples, understanding common multiples is crucial for solving various mathematical problems, particularly those involving fractions, least common multiples (LCM), and algebraic expressions. A common multiple of a set of numbers is a number that each of the numbers in the set divides without leaving a remainder. For example, the common multiples of 4 and 6 include 12, 24, 36, and so on. The smallest of these, 12, is known as the least common multiple (LCM). |
Numerical Expressions |

|
Definition--Factors and Multiples--Common Multiples | Common MultiplesTopicFactors and Multiples DefinitionA common multiple is a number that is a multiple of two or more numbers. DescriptionIn the context of factors and multiples, understanding common multiples is crucial for solving various mathematical problems, particularly those involving fractions, least common multiples (LCM), and algebraic expressions. A common multiple of a set of numbers is a number that each of the numbers in the set divides without leaving a remainder. For example, the common multiples of 4 and 6 include 12, 24, 36, and so on. The smallest of these, 12, is known as the least common multiple (LCM). |
Numerical Expressions |

|
Definition--Factors and Multiples--Common Multiples | Common MultiplesTopicFactors and Multiples DefinitionA common multiple is a number that is a multiple of two or more numbers. DescriptionIn the context of factors and multiples, understanding common multiples is crucial for solving various mathematical problems, particularly those involving fractions, least common multiples (LCM), and algebraic expressions. A common multiple of a set of numbers is a number that each of the numbers in the set divides without leaving a remainder. For example, the common multiples of 4 and 6 include 12, 24, 36, and so on. The smallest of these, 12, is known as the least common multiple (LCM). |
Numerical Expressions |

|
Definition--Factors and Multiples--Common Multiples | Common MultiplesTopicFactors and Multiples DefinitionA common multiple is a number that is a multiple of two or more numbers. DescriptionIn the context of factors and multiples, understanding common multiples is crucial for solving various mathematical problems, particularly those involving fractions, least common multiples (LCM), and algebraic expressions. A common multiple of a set of numbers is a number that each of the numbers in the set divides without leaving a remainder. For example, the common multiples of 4 and 6 include 12, 24, 36, and so on. The smallest of these, 12, is known as the least common multiple (LCM). |
Numerical Expressions |

|
Definition--Factors and Multiples--Common Multiples | Common MultiplesTopicFactors and Multiples DefinitionA common multiple is a number that is a multiple of two or more numbers. DescriptionIn the context of factors and multiples, understanding common multiples is crucial for solving various mathematical problems, particularly those involving fractions, least common multiples (LCM), and algebraic expressions. A common multiple of a set of numbers is a number that each of the numbers in the set divides without leaving a remainder. For example, the common multiples of 4 and 6 include 12, 24, 36, and so on. The smallest of these, 12, is known as the least common multiple (LCM). |
Numerical Expressions |

|
Definition--Factors and Multiples--Divisor | DivisorTopicFactors and Multiples DefinitionA divisor is a number that divides another number evenly, leaving no remainder. DescriptionIn the context of factors and multiples, a divisor plays a crucial role in understanding the relationships between numbers. A divisor is essentially a factor of a given number, as it divides that number without leaving a remainder. This concept is fundamental to identifying factors and understanding divisibility rules. |
Numerical Expressions |

|
Definition--Factors and Multiples--Divisor | DivisorTopicFactors and Multiples DefinitionA divisor is a number that divides another number evenly, leaving no remainder. DescriptionIn the context of factors and multiples, a divisor plays a crucial role in understanding the relationships between numbers. A divisor is essentially a factor of a given number, as it divides that number without leaving a remainder. This concept is fundamental to identifying factors and understanding divisibility rules. |
Numerical Expressions |

|
Definition--Factors and Multiples--Divisor | DivisorTopicFactors and Multiples DefinitionA divisor is a number that divides another number evenly, leaving no remainder. DescriptionIn the context of factors and multiples, a divisor plays a crucial role in understanding the relationships between numbers. A divisor is essentially a factor of a given number, as it divides that number without leaving a remainder. This concept is fundamental to identifying factors and understanding divisibility rules. |
Numerical Expressions |

|
Definition--Factors and Multiples--Divisor | DivisorTopicFactors and Multiples DefinitionA divisor is a number that divides another number evenly, leaving no remainder. DescriptionIn the context of factors and multiples, a divisor plays a crucial role in understanding the relationships between numbers. A divisor is essentially a factor of a given number, as it divides that number without leaving a remainder. This concept is fundamental to identifying factors and understanding divisibility rules. |
Numerical Expressions |

|
Definition--Factors and Multiples--Divisor | DivisorTopicFactors and Multiples DefinitionA divisor is a number that divides another number evenly, leaving no remainder. DescriptionIn the context of factors and multiples, a divisor plays a crucial role in understanding the relationships between numbers. A divisor is essentially a factor of a given number, as it divides that number without leaving a remainder. This concept is fundamental to identifying factors and understanding divisibility rules. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factor Pairs | Factor PairsTopicFactors and Multiples DefinitionFactor pairs are sets of two numbers that, when multiplied together, produce a given number. DescriptionFactor pairs play a crucial role in understanding the relationships between numbers and their factors. They are essential in various mathematical operations, particularly in algebra and number theory. Factor pairs help students visualize the multiplicative structure of numbers and provide a foundation for more advanced concepts such as prime factorization and divisibility rules. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factor Pairs | Factor PairsTopicFactors and Multiples DefinitionFactor pairs are sets of two numbers that, when multiplied together, produce a given number. DescriptionFactor pairs play a crucial role in understanding the relationships between numbers and their factors. They are essential in various mathematical operations, particularly in algebra and number theory. Factor pairs help students visualize the multiplicative structure of numbers and provide a foundation for more advanced concepts such as prime factorization and divisibility rules. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factor Pairs | Factor PairsTopicFactors and Multiples DefinitionFactor pairs are sets of two numbers that, when multiplied together, produce a given number. DescriptionFactor pairs play a crucial role in understanding the relationships between numbers and their factors. They are essential in various mathematical operations, particularly in algebra and number theory. Factor pairs help students visualize the multiplicative structure of numbers and provide a foundation for more advanced concepts such as prime factorization and divisibility rules. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factor Pairs | Factor PairsTopicFactors and Multiples DefinitionFactor pairs are sets of two numbers that, when multiplied together, produce a given number. DescriptionFactor pairs play a crucial role in understanding the relationships between numbers and their factors. They are essential in various mathematical operations, particularly in algebra and number theory. Factor pairs help students visualize the multiplicative structure of numbers and provide a foundation for more advanced concepts such as prime factorization and divisibility rules. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factor Pairs | Factor PairsTopicFactors and Multiples DefinitionFactor pairs are sets of two numbers that, when multiplied together, produce a given number. DescriptionFactor pairs play a crucial role in understanding the relationships between numbers and their factors. They are essential in various mathematical operations, particularly in algebra and number theory. Factor pairs help students visualize the multiplicative structure of numbers and provide a foundation for more advanced concepts such as prime factorization and divisibility rules. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factor Tree | Factor TreeTopicFactors and Multiples DefinitionA factor tree is a graphical method used to break down a number into its prime factors. DescriptionA factor tree is a visual representation that helps in identifying the prime factors of a given number. It starts with the original number at the top and branches downwards, breaking the number into its factors until all the branches end in prime numbers. This method is particularly useful in understanding the concept of prime factorization, which is the process of expressing a number as the product of its prime factors. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factor Tree | Factor TreeTopicFactors and Multiples DefinitionA factor tree is a graphical method used to break down a number into its prime factors. DescriptionA factor tree is a visual representation that helps in identifying the prime factors of a given number. It starts with the original number at the top and branches downwards, breaking the number into its factors until all the branches end in prime numbers. This method is particularly useful in understanding the concept of prime factorization, which is the process of expressing a number as the product of its prime factors. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factor Tree | Factor TreeTopicFactors and Multiples DefinitionA factor tree is a graphical method used to break down a number into its prime factors. DescriptionA factor tree is a visual representation that helps in identifying the prime factors of a given number. It starts with the original number at the top and branches downwards, breaking the number into its factors until all the branches end in prime numbers. This method is particularly useful in understanding the concept of prime factorization, which is the process of expressing a number as the product of its prime factors. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factor Tree | Factor TreeTopicFactors and Multiples DefinitionA factor tree is a graphical method used to break down a number into its prime factors. DescriptionA factor tree is a visual representation that helps in identifying the prime factors of a given number. It starts with the original number at the top and branches downwards, breaking the number into its factors until all the branches end in prime numbers. This method is particularly useful in understanding the concept of prime factorization, which is the process of expressing a number as the product of its prime factors. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factor Tree | Factor TreeTopicFactors and Multiples DefinitionA factor tree is a graphical method used to break down a number into its prime factors. DescriptionA factor tree is a visual representation that helps in identifying the prime factors of a given number. It starts with the original number at the top and branches downwards, breaking the number into its factors until all the branches end in prime numbers. This method is particularly useful in understanding the concept of prime factorization, which is the process of expressing a number as the product of its prime factors. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factoring Algebraic Expressions | Factoring Algebraic ExpressionsTopicFactors and Multiples DefinitionFactoring algebraic expressions involves breaking down a polynomial into simpler components called factors that, when multiplied together, give the original polynomial. DescriptionFactoring algebraic expressions is a fundamental concept in algebra that plays a crucial role in simplifying expressions, solving equations, and understanding polynomial functions. This process involves expressing a polynomial as a product of its factors, which are simpler polynomials or numbers. For instance, the polynomial x^2 - 5x + 6 can be factored into (x - 2)(x - 3). |
Numerical Expressions |

|
Definition--Factors and Multiples--Factoring Algebraic Expressions | Factoring Algebraic ExpressionsTopicFactors and Multiples DefinitionFactoring algebraic expressions involves breaking down a polynomial into simpler components called factors that, when multiplied together, give the original polynomial. DescriptionFactoring algebraic expressions is a fundamental concept in algebra that plays a crucial role in simplifying expressions, solving equations, and understanding polynomial functions. This process involves expressing a polynomial as a product of its factors, which are simpler polynomials or numbers. For instance, the polynomial x^2 - 5x + 6 can be factored into (x - 2)(x - 3). |
Numerical Expressions |

|
Definition--Factors and Multiples--Factoring Algebraic Expressions | Factoring Algebraic ExpressionsTopicFactors and Multiples DefinitionFactoring algebraic expressions involves breaking down a polynomial into simpler components called factors that, when multiplied together, give the original polynomial. DescriptionFactoring algebraic expressions is a fundamental concept in algebra that plays a crucial role in simplifying expressions, solving equations, and understanding polynomial functions. This process involves expressing a polynomial as a product of its factors, which are simpler polynomials or numbers. For instance, the polynomial x^2 - 5x + 6 can be factored into (x - 2)(x - 3). |
Numerical Expressions |

|
Definition--Factors and Multiples--Factoring Algebraic Expressions | Factoring Algebraic ExpressionsTopicFactors and Multiples DefinitionFactoring algebraic expressions involves breaking down a polynomial into simpler components called factors that, when multiplied together, give the original polynomial. DescriptionFactoring algebraic expressions is a fundamental concept in algebra that plays a crucial role in simplifying expressions, solving equations, and understanding polynomial functions. This process involves expressing a polynomial as a product of its factors, which are simpler polynomials or numbers. For instance, the polynomial x^2 - 5x + 6 can be factored into (x - 2)(x - 3). |
Numerical Expressions |