
Illustrative Math Alignment: Grade 6 Unit 1
Arithmetic in Base Ten
Lesson 6: Methods for Multiplying Decimals
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail | Title | Description | Curriculum Nodes |
|---|---|---|---|

|
Definition--Factors and Multiples--Factoring Algebraic Expressions | Factoring Algebraic ExpressionsTopicFactors and Multiples DefinitionFactoring algebraic expressions involves breaking down a polynomial into simpler components called factors that, when multiplied together, give the original polynomial. DescriptionFactoring algebraic expressions is a fundamental concept in algebra that plays a crucial role in simplifying expressions, solving equations, and understanding polynomial functions. This process involves expressing a polynomial as a product of its factors, which are simpler polynomials or numbers. For instance, the polynomial x^2 - 5x + 6 can be factored into (x - 2)(x - 3). |
Numerical Expressions |

|
Definition--Factors and Multiples--Factors | FactorsTopicFactors and Multiples DefinitionFactors are numbers that divide evenly into another number without leaving a remainder. DescriptionFactors play a crucial role in understanding the fundamental properties of numbers and their relationships. In the context of factors and multiples, factors are the building blocks that, when multiplied together, create a given number. This concept is essential for various mathematical operations and problem-solving techniques. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factors | FactorsTopicFactors and Multiples DefinitionFactors are numbers that divide evenly into another number without leaving a remainder. DescriptionFactors play a crucial role in understanding the fundamental properties of numbers and their relationships. In the context of factors and multiples, factors are the building blocks that, when multiplied together, create a given number. This concept is essential for various mathematical operations and problem-solving techniques. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factors | FactorsTopicFactors and Multiples DefinitionFactors are numbers that divide evenly into another number without leaving a remainder. DescriptionFactors play a crucial role in understanding the fundamental properties of numbers and their relationships. In the context of factors and multiples, factors are the building blocks that, when multiplied together, create a given number. This concept is essential for various mathematical operations and problem-solving techniques. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factors | FactorsTopicFactors and Multiples DefinitionFactors are numbers that divide evenly into another number without leaving a remainder. DescriptionFactors play a crucial role in understanding the fundamental properties of numbers and their relationships. In the context of factors and multiples, factors are the building blocks that, when multiplied together, create a given number. This concept is essential for various mathematical operations and problem-solving techniques. |
Numerical Expressions |

|
Definition--Factors and Multiples--Factors | FactorsTopicFactors and Multiples DefinitionFactors are numbers that divide evenly into another number without leaving a remainder. DescriptionFactors play a crucial role in understanding the fundamental properties of numbers and their relationships. In the context of factors and multiples, factors are the building blocks that, when multiplied together, create a given number. This concept is essential for various mathematical operations and problem-solving techniques. |
Numerical Expressions |

|
Definition--Factors and Multiples--Greatest Common Factor (GCF) | Greatest Common Factor (GCF)TopicFactors and Multiples DefinitionThe Greatest Common Factor (GCF) is the largest number that divides two or more numbers without leaving a remainder. DescriptionThe concept of the Greatest Common Factor (GCF) is crucial in the study of factors and multiples. The GCF is used to simplify fractions, find common denominators, and solve problems involving ratios. Understanding the GCF helps in breaking down complex problems into simpler parts, making it easier to handle large numbers and perform arithmetic operations efficiently. |
Numerical Expressions |

|
Definition--Factors and Multiples--Greatest Common Factor (GCF) | Greatest Common Factor (GCF)TopicFactors and Multiples DefinitionThe Greatest Common Factor (GCF) is the largest number that divides two or more numbers without leaving a remainder. DescriptionThe concept of the Greatest Common Factor (GCF) is crucial in the study of factors and multiples. The GCF is used to simplify fractions, find common denominators, and solve problems involving ratios. Understanding the GCF helps in breaking down complex problems into simpler parts, making it easier to handle large numbers and perform arithmetic operations efficiently. |
Numerical Expressions |

|
Definition--Factors and Multiples--Greatest Common Factor (GCF) | Greatest Common Factor (GCF)TopicFactors and Multiples DefinitionThe Greatest Common Factor (GCF) is the largest number that divides two or more numbers without leaving a remainder. DescriptionThe concept of the Greatest Common Factor (GCF) is crucial in the study of factors and multiples. The GCF is used to simplify fractions, find common denominators, and solve problems involving ratios. Understanding the GCF helps in breaking down complex problems into simpler parts, making it easier to handle large numbers and perform arithmetic operations efficiently. |
Numerical Expressions |

|
Definition--Factors and Multiples--Greatest Common Factor (GCF) | Greatest Common Factor (GCF)TopicFactors and Multiples DefinitionThe Greatest Common Factor (GCF) is the largest number that divides two or more numbers without leaving a remainder. DescriptionThe concept of the Greatest Common Factor (GCF) is crucial in the study of factors and multiples. The GCF is used to simplify fractions, find common denominators, and solve problems involving ratios. Understanding the GCF helps in breaking down complex problems into simpler parts, making it easier to handle large numbers and perform arithmetic operations efficiently. |
Numerical Expressions |

|
Definition--Factors and Multiples--Greatest Common Factor (GCF) | Greatest Common Factor (GCF)TopicFactors and Multiples DefinitionThe Greatest Common Factor (GCF) is the largest number that divides two or more numbers without leaving a remainder. DescriptionThe concept of the Greatest Common Factor (GCF) is crucial in the study of factors and multiples. The GCF is used to simplify fractions, find common denominators, and solve problems involving ratios. Understanding the GCF helps in breaking down complex problems into simpler parts, making it easier to handle large numbers and perform arithmetic operations efficiently. |
Numerical Expressions |

|
Definition--Factors and Multiples--Greatest Common Factor (GCF) | Greatest Common Factor (GCF)TopicFactors and Multiples DefinitionThe Greatest Common Factor (GCF) is the largest number that divides two or more numbers without leaving a remainder. DescriptionThe concept of the Greatest Common Factor (GCF) is crucial in the study of factors and multiples. The GCF is used to simplify fractions, find common denominators, and solve problems involving ratios. Understanding the GCF helps in breaking down complex problems into simpler parts, making it easier to handle large numbers and perform arithmetic operations efficiently. |
Numerical Expressions |

|
Definition--Factors and Multiples--LCM | Least Common Multiple (LCM)TopicFactors and Multiples DefinitionThe least common multiple (LCM) is the smallest number that is a multiple of two or more numbers. DescriptionThe concept of the least common multiple (LCM) is essential in the study of factors and multiples. The LCM of two or more numbers is the smallest number that is evenly divisible by all of the given numbers. This concept is particularly useful in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--LCM | Least Common Multiple (LCM)TopicFactors and Multiples DefinitionThe least common multiple (LCM) is the smallest number that is a multiple of two or more numbers. DescriptionThe concept of the least common multiple (LCM) is essential in the study of factors and multiples. The LCM of two or more numbers is the smallest number that is evenly divisible by all of the given numbers. This concept is particularly useful in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--LCM | Least Common Multiple (LCM)TopicFactors and Multiples DefinitionThe least common multiple (LCM) is the smallest number that is a multiple of two or more numbers. DescriptionThe concept of the least common multiple (LCM) is essential in the study of factors and multiples. The LCM of two or more numbers is the smallest number that is evenly divisible by all of the given numbers. This concept is particularly useful in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--LCM | Least Common Multiple (LCM)TopicFactors and Multiples DefinitionThe least common multiple (LCM) is the smallest number that is a multiple of two or more numbers. DescriptionThe concept of the least common multiple (LCM) is essential in the study of factors and multiples. The LCM of two or more numbers is the smallest number that is evenly divisible by all of the given numbers. This concept is particularly useful in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--LCM | Least Common Multiple (LCM)TopicFactors and Multiples DefinitionThe least common multiple (LCM) is the smallest number that is a multiple of two or more numbers. DescriptionThe concept of the least common multiple (LCM) is essential in the study of factors and multiples. The LCM of two or more numbers is the smallest number that is evenly divisible by all of the given numbers. This concept is particularly useful in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--LCM | Least Common Multiple (LCM)TopicFactors and Multiples DefinitionThe least common multiple (LCM) is the smallest number that is a multiple of two or more numbers. DescriptionThe concept of the least common multiple (LCM) is essential in the study of factors and multiples. The LCM of two or more numbers is the smallest number that is evenly divisible by all of the given numbers. This concept is particularly useful in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiple | MultiplesTopicFactors and Multiples DefinitionA multiple is a number that can be divided by another number without leaving a remainder. DescriptionMultiples are fundamental in understanding the relationships between numbers in mathematics. They are particularly relevant when learning about factors and multiples, which are key concepts in elementary and middle school math curricula. A multiple of a number is obtained by multiplying that number by an integer. For example, the multiples of 5 include 5, 10, 15, 20, and so on. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiple | MultiplesTopicFactors and Multiples DefinitionA multiple is a number that can be divided by another number without leaving a remainder. DescriptionMultiples are fundamental in understanding the relationships between numbers in mathematics. They are particularly relevant when learning about factors and multiples, which are key concepts in elementary and middle school math curricula. A multiple of a number is obtained by multiplying that number by an integer. For example, the multiples of 5 include 5, 10, 15, 20, and so on. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiple | MultiplesTopicFactors and Multiples DefinitionA multiple is a number that can be divided by another number without leaving a remainder. DescriptionMultiples are fundamental in understanding the relationships between numbers in mathematics. They are particularly relevant when learning about factors and multiples, which are key concepts in elementary and middle school math curricula. A multiple of a number is obtained by multiplying that number by an integer. For example, the multiples of 5 include 5, 10, 15, 20, and so on. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiple | MultiplesTopicFactors and Multiples DefinitionA multiple is a number that can be divided by another number without leaving a remainder. DescriptionMultiples are fundamental in understanding the relationships between numbers in mathematics. They are particularly relevant when learning about factors and multiples, which are key concepts in elementary and middle school math curricula. A multiple of a number is obtained by multiplying that number by an integer. For example, the multiples of 5 include 5, 10, 15, 20, and so on. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiple | MultiplesTopicFactors and Multiples DefinitionA multiple is a number that can be divided by another number without leaving a remainder. DescriptionMultiples are fundamental in understanding the relationships between numbers in mathematics. They are particularly relevant when learning about factors and multiples, which are key concepts in elementary and middle school math curricula. A multiple of a number is obtained by multiplying that number by an integer. For example, the multiples of 5 include 5, 10, 15, 20, and so on. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of 10 | Multiples of 10TopicFactors and Multiples DefinitionMultiples of 10 are the numbers that result from multiplying 10 by any whole number. DescriptionMultiples of 10 play a significant role in understanding factors and multiples. These numbers are easily recognizable as they always end in zero and form a predictable pattern on the number line. In the context of factors and multiples, multiples of 10 serve as an excellent example to illustrate the concept of multiples in general. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of 10 | Multiples of 10TopicFactors and Multiples DefinitionMultiples of 10 are the numbers that result from multiplying 10 by any whole number. DescriptionMultiples of 10 play a significant role in understanding factors and multiples. These numbers are easily recognizable as they always end in zero and form a predictable pattern on the number line. In the context of factors and multiples, multiples of 10 serve as an excellent example to illustrate the concept of multiples in general. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of 10 | Multiples of 10TopicFactors and Multiples DefinitionMultiples of 10 are the numbers that result from multiplying 10 by any whole number. DescriptionMultiples of 10 play a significant role in understanding factors and multiples. These numbers are easily recognizable as they always end in zero and form a predictable pattern on the number line. In the context of factors and multiples, multiples of 10 serve as an excellent example to illustrate the concept of multiples in general. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of 10 | Multiples of 10TopicFactors and Multiples DefinitionMultiples of 10 are the numbers that result from multiplying 10 by any whole number. DescriptionMultiples of 10 play a significant role in understanding factors and multiples. These numbers are easily recognizable as they always end in zero and form a predictable pattern on the number line. In the context of factors and multiples, multiples of 10 serve as an excellent example to illustrate the concept of multiples in general. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of 10 | Multiples of 10TopicFactors and Multiples DefinitionMultiples of 10 are the numbers that result from multiplying 10 by any whole number. DescriptionMultiples of 10 play a significant role in understanding factors and multiples. These numbers are easily recognizable as they always end in zero and form a predictable pattern on the number line. In the context of factors and multiples, multiples of 10 serve as an excellent example to illustrate the concept of multiples in general. |
Numerical Expressions |
|
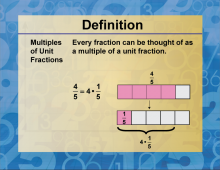
Definition--Factors and Multiples--Multiples of Unit Fractions | Multiples of Unit FractionsTopicFactors and Multiples DefinitionMultiples are the results obtained when a number is multiplied by an integer. DescriptionIn mathematics, understanding the concept of multiples is crucial, especially when dealing with factors and multiples. A multiple of a number is the product obtained when that number is multiplied by an integer. For example, the multiples of 3 include 3, 6, 9, 12, and so on. This concept is fundamental in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of Unit Fractions | Multiples of Unit FractionsTopicFactors and Multiples DefinitionMultiples are the results obtained when a number is multiplied by an integer. DescriptionIn mathematics, understanding the concept of multiples is crucial, especially when dealing with factors and multiples. A multiple of a number is the product obtained when that number is multiplied by an integer. For example, the multiples of 3 include 3, 6, 9, 12, and so on. This concept is fundamental in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of Unit Fractions | Multiples of Unit FractionsTopicFactors and Multiples DefinitionMultiples are the results obtained when a number is multiplied by an integer. DescriptionIn mathematics, understanding the concept of multiples is crucial, especially when dealing with factors and multiples. A multiple of a number is the product obtained when that number is multiplied by an integer. For example, the multiples of 3 include 3, 6, 9, 12, and so on. This concept is fundamental in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of Unit Fractions | Multiples of Unit FractionsTopicFactors and Multiples DefinitionMultiples are the results obtained when a number is multiplied by an integer. DescriptionIn mathematics, understanding the concept of multiples is crucial, especially when dealing with factors and multiples. A multiple of a number is the product obtained when that number is multiplied by an integer. For example, the multiples of 3 include 3, 6, 9, 12, and so on. This concept is fundamental in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--Multiples of Unit Fractions | Multiples of Unit FractionsTopicFactors and Multiples DefinitionMultiples are the results obtained when a number is multiplied by an integer. DescriptionIn mathematics, understanding the concept of multiples is crucial, especially when dealing with factors and multiples. A multiple of a number is the product obtained when that number is multiplied by an integer. For example, the multiples of 3 include 3, 6, 9, 12, and so on. This concept is fundamental in various mathematical operations and problem-solving scenarios. |
Numerical Expressions |

|
Definition--Factors and Multiples--Prime Factorization | Prime FactorizationTopicFactors and Multiples DefinitionPrime factorization is the process of breaking down a composite number into its prime factors. DescriptionPrime factorization is a fundamental concept in the study of factors and multiples. It involves expressing a composite number as a product of prime numbers. For example, the number 60 can be factorized into 2 × 2 × 3 × 5. This process is crucial because it provides a unique representation of numbers, which is essential in various mathematical applications, including simplifying fractions, finding least common multiples (LCM), and greatest common divisors (GCD). |
Numerical Expressions |

|
Definition--Factors and Multiples--Prime Factorization | Prime FactorizationTopicFactors and Multiples DefinitionPrime factorization is the process of breaking down a composite number into its prime factors. DescriptionPrime factorization is a fundamental concept in the study of factors and multiples. It involves expressing a composite number as a product of prime numbers. For example, the number 60 can be factorized into 2 × 2 × 3 × 5. This process is crucial because it provides a unique representation of numbers, which is essential in various mathematical applications, including simplifying fractions, finding least common multiples (LCM), and greatest common divisors (GCD). |
Numerical Expressions |

|
Definition--Factors and Multiples--Prime Factorization | Prime FactorizationTopicFactors and Multiples DefinitionPrime factorization is the process of breaking down a composite number into its prime factors. DescriptionPrime factorization is a fundamental concept in the study of factors and multiples. It involves expressing a composite number as a product of prime numbers. For example, the number 60 can be factorized into 2 × 2 × 3 × 5. This process is crucial because it provides a unique representation of numbers, which is essential in various mathematical applications, including simplifying fractions, finding least common multiples (LCM), and greatest common divisors (GCD). |
Numerical Expressions |

|
Definition--Factors and Multiples--Prime Factorization | Prime FactorizationTopicFactors and Multiples DefinitionPrime factorization is the process of breaking down a composite number into its prime factors. DescriptionPrime factorization is a fundamental concept in the study of factors and multiples. It involves expressing a composite number as a product of prime numbers. For example, the number 60 can be factorized into 2 × 2 × 3 × 5. This process is crucial because it provides a unique representation of numbers, which is essential in various mathematical applications, including simplifying fractions, finding least common multiples (LCM), and greatest common divisors (GCD). |
Numerical Expressions |

|
Definition--Factors and Multiples--Prime Factorization | Prime FactorizationTopicFactors and Multiples DefinitionPrime factorization is the process of breaking down a composite number into its prime factors. DescriptionPrime factorization is a fundamental concept in the study of factors and multiples. It involves expressing a composite number as a product of prime numbers. For example, the number 60 can be factorized into 2 × 2 × 3 × 5. This process is crucial because it provides a unique representation of numbers, which is essential in various mathematical applications, including simplifying fractions, finding least common multiples (LCM), and greatest common divisors (GCD). |
Numerical Expressions |

|
Definition--Factors and Multiples--Prime Factors | Prime FactorsTopicFactors and Multiples DefinitionPrime factors are the prime numbers that multiply together to give the original number. DescriptionPrime factors are a fundamental concept in the study of factors and multiples. They are the building blocks of all numbers, as any integer greater than 1 can be expressed as a product of prime numbers. This process is known as prime factorization. For example, the prime factorization of 28 is 2 × 2 × 7, where 2 and 7 are prime numbers. |
Numerical Expressions |

|
Definition--Factors and Multiples--Prime Factors | Prime FactorsTopicFactors and Multiples DefinitionPrime factors are the prime numbers that multiply together to give the original number. DescriptionPrime factors are a fundamental concept in the study of factors and multiples. They are the building blocks of all numbers, as any integer greater than 1 can be expressed as a product of prime numbers. This process is known as prime factorization. For example, the prime factorization of 28 is 2 × 2 × 7, where 2 and 7 are prime numbers. |
Numerical Expressions |

|
Definition--Factors and Multiples--Prime Factors | Prime FactorsTopicFactors and Multiples DefinitionPrime factors are the prime numbers that multiply together to give the original number. DescriptionPrime factors are a fundamental concept in the study of factors and multiples. They are the building blocks of all numbers, as any integer greater than 1 can be expressed as a product of prime numbers. This process is known as prime factorization. For example, the prime factorization of 28 is 2 × 2 × 7, where 2 and 7 are prime numbers. |
Numerical Expressions |

|
Definition--Factors and Multiples--Prime Factors | Prime FactorsTopicFactors and Multiples DefinitionPrime factors are the prime numbers that multiply together to give the original number. DescriptionPrime factors are a fundamental concept in the study of factors and multiples. They are the building blocks of all numbers, as any integer greater than 1 can be expressed as a product of prime numbers. This process is known as prime factorization. For example, the prime factorization of 28 is 2 × 2 × 7, where 2 and 7 are prime numbers. |
Numerical Expressions |

|
Definition--Factors and Multiples--Prime Factors | Prime FactorsTopicFactors and Multiples DefinitionPrime factors are the prime numbers that multiply together to give the original number. DescriptionPrime factors are a fundamental concept in the study of factors and multiples. They are the building blocks of all numbers, as any integer greater than 1 can be expressed as a product of prime numbers. This process is known as prime factorization. For example, the prime factorization of 28 is 2 × 2 × 7, where 2 and 7 are prime numbers. |
Numerical Expressions |

|
Definition--Factors and Multiples--Prime Factors | Prime FactorsTopicFactors and Multiples DefinitionPrime factors are the prime numbers that multiply together to give the original number. DescriptionPrime factors are a fundamental concept in the study of factors and multiples. They are the building blocks of all numbers, as any integer greater than 1 can be expressed as a product of prime numbers. This process is known as prime factorization. For example, the prime factorization of 28 is 2 × 2 × 7, where 2 and 7 are prime numbers. |
Numerical Expressions |

|
Definition--Factors and Multiples--Proper Factors | Proper FactorsTopicFactors and Multiples DefinitionProper factors are the factors of a number excluding the number itself and 1. DescriptionProper factors play a significant role in the study of factors and multiples. Understanding proper factors is essential for grasping more complex mathematical concepts such as prime factorization, greatest common divisors, and least common multiples. |
Numerical Expressions |

|
Definition--Factors and Multiples--Proper Factors | Proper FactorsTopicFactors and Multiples DefinitionProper factors are the factors of a number excluding the number itself and 1. DescriptionProper factors play a significant role in the study of factors and multiples. Understanding proper factors is essential for grasping more complex mathematical concepts such as prime factorization, greatest common divisors, and least common multiples. |
Numerical Expressions |

|
Definition--Factors and Multiples--Proper Factors | Proper FactorsTopicFactors and Multiples DefinitionProper factors are the factors of a number excluding the number itself and 1. DescriptionProper factors play a significant role in the study of factors and multiples. Understanding proper factors is essential for grasping more complex mathematical concepts such as prime factorization, greatest common divisors, and least common multiples. |
Numerical Expressions |

|
Definition--Factors and Multiples--Proper Factors | Proper FactorsTopicFactors and Multiples DefinitionProper factors are the factors of a number excluding the number itself and 1. DescriptionProper factors play a significant role in the study of factors and multiples. Understanding proper factors is essential for grasping more complex mathematical concepts such as prime factorization, greatest common divisors, and least common multiples. |
Numerical Expressions |

|
Definition--Factors and Multiples--Proper Factors | Proper FactorsTopicFactors and Multiples DefinitionProper factors are the factors of a number excluding the number itself and 1. DescriptionProper factors play a significant role in the study of factors and multiples. Understanding proper factors is essential for grasping more complex mathematical concepts such as prime factorization, greatest common divisors, and least common multiples. |
Numerical Expressions |

|
Definition--Factors and Multiples--Simplifying Fractions Using Factoring | Simplifying Fractions with FactoringTopicFactors and Multiples DefinitionSimplifying fractions involves reducing the fraction to its simplest form by dividing both the numerator and the denominator by their greatest common factor (GCF). |
Numerical Expressions |