Illustrative Math Alignment: Grade 6 Unit 1

Arithmetic in Base Ten

Lesson 6: Methods for Multiplying Decimals

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Description	Curriculum Nodes
Closed Captioned Video: Integers: What Are Integers?	Closed Captioned Video: Integers: What Are Integers? Video Tutorial: Integers: What Are Integers? In this video, students learn the basic definition of an integer and look at real-world applications of them. This is part of a series of videos on the topic of Integers. This includes defining integers, modeling integers, integer operations, and integer expressions. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on integers, click on this link. The following section includes background information on integers (and also rational numbers). Refer to this section as you view the videos, or as review material afterward.	Numerical Expressions
Closed Captioned Video: Integers: What Are Integers?	Closed Captioned Video: Integers: What Are Integers? Video Tutorial: Integers: What Are Integers? In this video, students learn the basic definition of an integer and look at real-world applications of them. This is part of a series of videos on the topic of Integers. This includes defining integers, modeling integers, integer operations, and integer expressions. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on integers, click on this link. The following section includes background information on integers (and also rational numbers). Refer to this section as you view the videos, or as review material afterward.	Numerical Expressions
Definition--Absolute Value	Definition--Absolute Value This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions
Definition--Absolute Value	Definition--Absolute Value This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions
Definition--Absolute Value	Definition--Absolute Value This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions
Definition--Additive Inverse	Definition--Additive Inverse This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions and Variable Expressions
Definition--Additive Inverse	Definition--Additive Inverse This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions and Variable Expressions
Definition--Additive Inverse	Definition--Additive Inverse This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions and Variable Expressions
Definition--Algebra	Definition--Algebra This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions and Variable Expressions
Definition--Algebra	Definition--Algebra This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions and Variable Expressions
Definition--Algebraic Fraction	Definition--Algebraic Fraction This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions and Variable Expressions
Definition--Algebraic Fraction	Definition--Algebraic Fraction This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions and Variable Expressions
Definition--Algorithm	Definition--Algorithm This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions and Variable Expressions
Definition--Algorithm	Definition--Algorithm This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions and Variable Expressions
Definition--Closure Property	Definition--Closure Property This is part of a collection of definitions on the topic of closure. This collection includes closure under the four basic operations, as well as for even numbers, odd numbers, whole numbers, integers, fractions, rational numbers, real number, and complex numbers.	Numerical Expressions
Definition--Closure Property	Definition--Closure Property This is part of a collection of definitions on the topic of closure. This collection includes closure under the four basic operations, as well as for even numbers, odd numbers, whole numbers, integers, fractions, rational numbers, real number, and complex numbers.	Numerical Expressions
Definition--Closure Property Topics--Closure Property	Closure Property Topic Math Properties Definition The closure property in mathematics states that a set is closed under an operation if performing that operation on any elements of the set always results in another element within the same set. This fundamental concept is essential in defining mathematical structures and understanding the behavior of number systems.	Numerical Expressions
Definition--Closure Property Topics--Complex Numbers and Closure: Addition	Complex Numbers and Closure: Addition Topic Math Properties Definition The closure property for addition of complex numbers states that the sum of any two complex numbers is always another complex number. This property ensures that the set of complex numbers is closed under addition, maintaining the integrity of the complex number system.	Numerical Expressions
Definition--Closure Property Topics--Complex Numbers and Closure: Division	Complex Numbers and Closure: Division Topic Math Properties Definition The closure property for division of complex numbers states that the quotient of any two complex numbers, where the divisor is non-zero, is always another complex number. This property ensures that the set of complex numbers is closed under division, maintaining the integrity of the complex number system.	Numerical Expressions
Definition--Closure Property Topics--Complex Numbers and Closure: Multiplication	Complex Numbers and Closure: Multiplication Topic Math Properties Definition The closure property for multiplication of complex numbers states that the product of any two complex numbers is always another complex number. This property ensures that the set of complex numbers is closed under multiplication, maintaining the integrity and consistency of the complex number system.	Numerical Expressions
Definition--Closure Property Topics--Complex Numbers and Closure: Subtraction	Definition--Closure Property Topics--Complex Numbers and Closure: Subtraction This is part of a collection of definitions on the topic of closure. This collection includes closure under the four basic operations, as well as for even numbers, odd numbers, whole numbers, integers, fractions, rational numbers, real number, and complex numbers.	Numerical Expressions
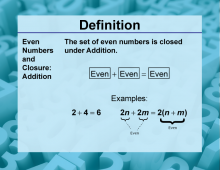
Definition--Closure Property Topics--Even Numbers and Closure: Addition	Even Numbers and Closure: Addition Topic Math Properties Definition The closure property for addition of even numbers states that the sum of any two even numbers is always an even number. Description The closure property for addition of even numbers is a fundamental concept in number theory and algebra. It demonstrates that the set of even numbers is closed under the operation of addition, meaning that when you add any two even numbers, the result will always be an even number.	Numerical Expressions
Definition--Closure Property Topics--Even Numbers and Closure: Division	Even Numbers and Closure: Division Topic Math Properties Definition The set of even numbers is not closed under division, meaning that dividing one even number by another does not always result in an even number. Description The concept of closure for even numbers under division is an important topic in number theory and algebra. Unlike addition and multiplication, division does not maintain closure within the set of even numbers. This means that when you divide one even number by another even number, the result is not always an even number.	Numerical Expressions
Definition--Closure Property Topics--Even Numbers and Closure: Multiplication	Even Numbers and Closure: Multiplication Topic Math Properties Definition The closure property for multiplication of even numbers states that the product of any two even numbers is always an even number. Description The closure property for multiplication of even numbers is a fundamental concept in number theory and algebra. It demonstrates that the set of even numbers is closed under the operation of multiplication, meaning that when you multiply any two even numbers, the result will always be an even number.	Numerical Expressions
Definition--Closure Property Topics--Even Numbers and Closure: Subtraction	Even Numbers and Closure: Subtraction Topic Math Properties Definition The closure property for subtraction of even numbers states that the difference between any two even numbers is always an even number. Description The closure property for subtraction of even numbers is a fundamental concept in number theory and algebra. It demonstrates that the set of even numbers is closed under the operation of subtraction, meaning that when you subtract any even number from another even number, the result will always be an even number.	Numerical Expressions
Definition--Closure Property Topics--Fractions and Closure: Addition	Fractions and Closure: Addition Topic Math Properties Definition The closure property for addition of fractions states that the sum of any two fractions is always another fraction. Description The closure property for addition of fractions is a fundamental concept in mathematics that demonstrates the consistency and completeness of the fraction number system. This property ensures that when we add any two fractions, the result is always another fraction, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Fractions and Closure: Division	Fractions and Closure: Division Topic Math Properties Definition The closure property for division of fractions states that the quotient of any two fractions (where the divisor is not zero) is always another fraction. Description The closure property for division of fractions is a crucial concept in mathematics that demonstrates the robustness of the fraction number system. This property ensures that when we divide one fraction by another (non-zero) fraction, the result is always another fraction, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Fractions and Closure: Multiplication	Fractions and Closure: Multiplication Topic Math Properties Definition The closure property for multiplication of fractions states that the product of any two fractions is always another fraction. Description The closure property for multiplication of fractions is a fundamental concept in mathematics that illustrates the consistency and completeness of the fraction number system. This property ensures that when we multiply any two fractions, the result is always another fraction, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Fractions and Closure: Subtraction	Fractions and Closure: Subtraction Topic Math Properties Definition The closure property for subtraction of fractions states that the difference between any two fractions is always another fraction. Description The closure property for subtraction of fractions is a fundamental concept in mathematics that demonstrates the consistency and completeness of the fraction number system. This property ensures that when we subtract one fraction from another, the result is always another fraction, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Integers and Closure: Addition	Integers and Closure: Addition Topic Math Properties Definition The closure property for addition of integers states that the sum of any two integers is always another integer. Description The closure property for addition of integers is a fundamental concept in mathematics that demonstrates the completeness of the integer number system. This property ensures that when we add any two integers, whether positive, negative, or zero, the result is always another integer, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Integers and Closure: Division	Integers and Closure: Division Topic Math Properties Definition The set of integers is not closed under division, meaning that the quotient of two integers is not always an integer. Description The concept of closure for integer division is unique among the basic arithmetic operations because it demonstrates a limitation of the integer number system. Unlike addition, subtraction, and multiplication, division does not always produce an integer result when performed on two integers.	Numerical Expressions
Definition--Closure Property Topics--Integers and Closure: Multiplication	Integers and Closure: Multiplication Topic Math Properties Definition The closure property for multiplication of integers states that the product of any two integers is always another integer. Description The closure property for multiplication of integers is a fundamental concept in mathematics that demonstrates the completeness of the integer number system. This property ensures that when we multiply any two integers, whether positive, negative, or zero, the result is always another integer, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Integers and Closure: Subtraction	Integers and Closure: Subtraction Topic Math Properties Definition The closure property for subtraction of integers states that the difference between any two integers is always another integer. Description The closure property for subtraction of integers is a fundamental concept in mathematics that demonstrates the completeness of the integer number system. This property ensures that when we subtract one integer from another, whether positive, negative, or zero, the result is always another integer, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Odd Numbers and Closure: Addition	Odd Numbers and Closure: Addition Topic Math Properties Definition The set of odd numbers is not closed under addition, meaning that the sum of two odd numbers is always an even number, not an odd number. Description The concept of closure for odd numbers under addition is an important property in number theory. It demonstrates that while odd numbers have many interesting properties, they do not form a closed system under addition. This property helps students understand the relationships between odd and even numbers and introduces them to the concept of parity.	Numerical Expressions
Definition--Closure Property Topics--Odd Numbers and Closure: Division	Odd Numbers and Closure: Division Topic Math Properties Definition The set of odd numbers is not closed under division, meaning that the quotient of two odd numbers is not always an odd number. Description The concept of closure for odd numbers under division is an important property in number theory. It demonstrates that odd numbers do not form a closed system under division. This property helps students understand the relationships between odd and even numbers and introduces them to the concept of rational numbers.	Numerical Expressions
Definition--Closure Property Topics--Odd Numbers and Closure: Multiplication	Odd Numbers and Closure: Multiplication Topic Math Properties Definition The set of odd numbers is closed under multiplication, meaning that the product of any two odd numbers is always an odd number. Description The closure property for multiplication of odd numbers is a fundamental concept in number theory. This property demonstrates that when we multiply any two odd numbers, the result is always another odd number, keeping us within the set of odd numbers.	Numerical Expressions
Definition--Closure Property Topics--Odd Numbers and Closure: Subtraction	Odd Numbers and Closure: Subtraction Topic Math Properties Definition The set of odd numbers is not closed under subtraction, meaning that the difference between two odd numbers is always an even number, not an odd number. Description The concept of closure for odd numbers under subtraction is an important property in number theory. It demonstrates that while odd numbers have many interesting properties, they do not form a closed system under subtraction. This property helps students understand the relationships between odd and even numbers and introduces them to the concept of parity.	Numerical Expressions
Definition--Closure Property Topics--Rational Numbers and Closure: Addition	Definition--Closure Property Topics--Rational Numbers and Closure: Addition This is part of a collection of definitions on the topic of closure. This collection includes closure under the four basic operations, as well as for even numbers, odd numbers, whole numbers, integers, fractions, rational numbers, real number, and complex numbers.	Numerical Expressions
Definition--Closure Property Topics--Rational Numbers and Closure: Division	Rational Numbers and Closure: Division Topic Math Properties Definition The closure property for division of rational numbers states that the quotient of any two rational numbers (where the divisor is not zero) is always another rational number. Description The closure property for division of rational numbers is a crucial concept in mathematics that demonstrates the robustness of the rational number system. This property ensures that when we divide one rational number by another (non-zero) rational number, the result is always another rational number, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Rational Numbers and Closure: Multiplication	Rational Numbers and Closure: Multiplication Topic Math Properties Definition The closure property for multiplication of rational numbers states that the product of any two rational numbers is always another rational number. Description The closure property for multiplication of rational numbers is a fundamental concept in mathematics that illustrates the consistency and completeness of the rational number system. This property ensures that when we multiply any two rational numbers, the result is always another rational number, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Rational Numbers and Closure: Subtraction	Rational Numbers and Closure: Subtraction Topic Math Properties Definition The closure property for subtraction of rational numbers states that the difference between any two rational numbers is always another rational number. Description The closure property for subtraction of rational numbers is a key concept in mathematics that demonstrates the consistency and completeness of the rational number system. This property ensures that when we subtract one rational number from another, the result is always another rational number, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Real Numbers and Closure: Addition	Real Numbers and Closure: Addition Topic Math Properties Definition The closure property for addition of real numbers states that the sum of any two real numbers is always another real number. Description The closure property for addition of real numbers is a fundamental concept in mathematics that demonstrates the consistency and completeness of the real number system. This property ensures that when we add any two real numbers, the result is always another real number, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Real Numbers and Closure: Division	Real Numbers and Closure: Division Topic Math Properties Definition The closure property for division of real numbers states that the quotient of any two real numbers (where the divisor is not zero) is always another real number. Description The closure property for division of real numbers is a crucial concept in mathematics that demonstrates the robustness of the real number system. This property ensures that when we divide one real number by another (non-zero) real number, the result is always another real number, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Real Numbers and Closure: Multiplication	Real Numbers and Closure: Multiplication Topic Math Properties Definition The closure property for multiplication of real numbers states that the product of any two real numbers is always another real number. Description The closure property for multiplication of real numbers is a fundamental concept in mathematics that illustrates the consistency and completeness of the real number system. This property ensures that when we multiply any two real numbers, the result is always another real number, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Real Numbers and Closure: Subtraction	Real Numbers and Closure: Subtraction Topic Math Properties Definition The closure property for subtraction of real numbers states that the difference between any two real numbers is always another real number. Description The closure property for subtraction of real numbers is a fundamental concept in mathematics that demonstrates the consistency and completeness of the real number system. This property ensures that when we subtract one real number from another, the result is always another real number, keeping us within the same number system.	Numerical Expressions
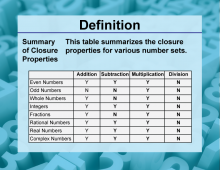
Definition--Closure Property Topics--Summary of Closure Properties	Summary of Closure Properties Topic Math Properties Definition The closure property refers to the characteristic of a set being closed under a specific operation, meaning that performing the operation on elements of the set results in an element that is also within the set. Description This summary encapsulates the closure properties across various number systems, including even numbers, odd numbers, whole numbers, integers, fractions, rational numbers, real numbers, and complex numbers. Each of these systems exhibits closure under certain operations, such as addition, subtraction, multiplication, and division, while failing to do so under others.	Numerical Expressions
Definition--Closure Property Topics--Whole Numbers and Closure: Addition	Whole Numbers and Closure: Addition Topic Math Properties Definition The closure property for addition of whole numbers states that the sum of any two whole numbers is always another whole number. Description The closure property for addition of whole numbers is a fundamental concept in mathematics that demonstrates the consistency and completeness of the whole number system. This property ensures that when we add any two whole numbers, the result is always another whole number, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Whole Numbers and Closure: Division	Whole Numbers and Closure: Division Topic Math Properties Definition The set of whole numbers is not closed under division, meaning that the quotient of two whole numbers is not always a whole number. Description The concept of closure for whole numbers under division is an important property in mathematics. It demonstrates that while whole numbers have many interesting properties, they do not form a closed system under division. This property helps students understand the relationships between whole numbers and introduces them to the concept of rational numbers.	Numerical Expressions
Definition--Closure Property Topics--Whole Numbers and Closure: Multiplication	Whole Numbers and Closure: Multiplication Topic Math Properties Definition The closure property for multiplication of whole numbers states that the product of any two whole numbers is always another whole number. Description The closure property for multiplication of whole numbers is a fundamental concept in mathematics that demonstrates the consistency and completeness of the whole number system. This property ensures that when we multiply any two whole numbers, the result is always another whole number, keeping us within the same number system.	Numerical Expressions
Definition--Closure Property Topics--Whole Numbers and Closure: Subtraction	Whole Numbers and Closure: Subtraction Topic Math Properties Definition The set of whole numbers is not closed under subtraction, meaning that the difference between two whole numbers is not always a whole number. Description The concept of closure for whole numbers under subtraction is an important property in mathematics. It demonstrates that while whole numbers have many interesting properties, they do not form a closed system under subtraction. This property helps students understand the relationships between whole numbers and introduces them to the concept of integers.	Numerical Expressions