Illustrative Math Alignment: Grade 6 Unit 1

Topic

Equations

Definition

The unknown is the variable in an equation that needs to be solved for.

Description

The unknown in an equation represents the value that needs to be determined. For example, in the equation 

x + 3 = 7

x is the unknown. Identifying and solving for the unknown is a core aspect of algebra.

In real-world applications, finding the unknown is crucial for solving problems in various fields such as science, engineering, and finance. Understanding how to identify and solve for the unknown helps students develop problem-solving skills and apply mathematical concepts to real-life situations.

Topic

Equations

Definition

The Transitive Property of Equality states that if a = b and b = c, then a = c.

Description

The Transitive Property of Equality is a fundamental principle in mathematics. It states that if one quantity equals a second quantity, and the second quantity equals a third, then the first and third quantities are equal. For example, if 

x = y

and

y = z

then 

x = z

This property is used to justify steps in solving equations and proving mathematical statements.

Topic

Equations

Definition

A true equation is an equation that holds true for the given values of the variable(s).

Description

A true equation is an equation that is valid for specific values of the variable(s). For example, the equation 

2 + 3 = 5

is true because both sides are equal. Identifying true equations is important in verifying the correctness of mathematical statements.

In real-world applications, recognizing true equations helps in ensuring the accuracy of mathematical models and solutions. Understanding true equations helps students develop critical thinking and analytical skills.

Topic

Equations

Definition

A two-step equation requires two operations to solve.

Description

Two-step equations involve performing two operations to isolate the variable. For example, solving 

2x + 3 = 7

requires subtracting 3 from both sides and then dividing by 2 to find x = 2. These equations are common in algebra and require a systematic approach to solve.

In real-world applications, two-step equations are used in problem-solving scenarios such as calculating costs or determining measurements. Understanding how to solve two-step equations helps students develop critical thinking and problem-solving skills.

Topic

Equations

Definition

A variable expression is a mathematical phrase involving variables, numbers, and operation symbols.

Description

Variable expressions consist of variables, numbers, and operations such as addition, subtraction, multiplication, and division. For example, 

3x + 4

is a variable expression. These expressions are used to represent quantities and relationships in algebra.

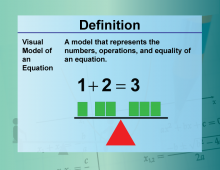
Topic

Equations

Definition

Visual models for equations use graphical representations to illustrate the relationships between variables.

Description

Visual models for equations include graphs, charts, and diagrams that represent the relationships between variables. For example, a graph of the equation 

y = 2x + 3

shows a straight line with a slope of 2 and a y-intercept of 3. These models help in understanding and interpreting equations.

The complete set of 13 examples that make up this set of tutorials.

Library of Instructional Resources

To see the complete library of Instructional Resources , click on this link.

The complete set of 42 examples that make up this set of tutorials.

Library of Instructional Resources

To see the complete library of Instructional Resources , click on this link.

The complete set of 21 examples that make up this set of tutorials.

Library of Instructional Resources

To see the complete library of Instructional Resources , click on this link.

Learn how to solve addition and subtraction equations using column addition and subtraction techniques.

Library of Instructional Resources

To see the complete library of Instructional Resources , click on this link.

This tutorial provides an overview of solving division equations, with the focus on one- and two-step equations.

Library of Instructional Resources

To see the complete library of Instructional Resources , click on this link.

This tutorial provides an overview of writing and solving multiplication equations. The focus is on one- and two-step equations.

Library of Instructional Resources

To see the complete library of Instructional Resources , click on this link.

Topic

Quadratics

Topic

Quadratics

Description

This example illustrates a quadratic with two real roots. The discriminant being positive indicates that there are two real solutions to the equation. This scenario helps students recognize the significance of repeated roots and their graphical representation.

For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.

Topic

Quadratics

Topic

Quadratics

Description

This example demonstrates a quadratic equation with one distinct real root, highlighting the relationship between the coefficients and the resulting discriminant. By calculating the discriminant, students can identify the nature of the roots, which is crucial for solving quadratics effectively. Skills involved include algebraic manipulation and understanding the graphical implications of roots.

For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.

Topic

Quadratics

Description

This example illustrates a quadratic with two real roots. The discriminant being positive indicates that there are two real roots. This scenario helps students recognize the significance of repeated roots and their graphical representation.

For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.

Topic

Quadratics

Description

This example demonstrates a quadratic equation with no distinct real roots, highlighting the relationship between the coefficients and the resulting discriminant. By calculating the discriminant, students can identify the nature of the roots, which is crucial for solving quadratics effectively. Skills involved include algebraic manipulation and understanding the graphical implications of roots.

For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.

Topic

Quadratics

Description

This example illustrates a quadratic with a double real root. The discriminant being zero indicates that there is exactly one real solution to the equation. This scenario helps students recognize the significance of repeated roots and their graphical representation.

For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.

Topic

Quadratics

Description

In this example, the quadratic equation results in two roots, demonstrating the cases where the discriminant is positive. This provides insights into scenarios where quadratic equations intersect the x-axis twice. Skills in algebra are focused on interpreting complex solutions and their geometric implications.

For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.

Topic

Quadratics

Description

This example illustrates a quadratic with two real roots. The discriminant being positive indicates that there are two real solutions to the equation. This scenario helps students recognize the significance of two roots and their graphical representation.

For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.

Topic

Quadratics

Description

This example demonstrates a quadratic equation with two distinct real roots, highlighting the relationship between the coefficients and the resulting discriminant. By calculating the discriminant, students can identify the nature of the roots, which is crucial for solving quadratics effectively. Skills involved include algebraic manipulation and understanding the graphical implications of roots.

For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to solve a proportion problem where two ratios a:b and c:d are proportional. Given the values b = 3, c = 4, and d = 6, we need to find the value of a. The proportion is set up as a / 3 = 4 / 6, which is then solved to find that a = 2.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar triangles with algebraic expressions. Two triangles are shown, one with sides of 6 and 9, and the other with sides of 2x and 2x + 9. The problem requires setting up a proportion: 6 / 9 = 2x / (2x + 9). Solving this equation leads to x = 9, which then allows us to find the side lengths of 18 and 27.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, one with legs of 7 and 9, and the other with legs of 14 and x. The problem requires finding the length of side x by setting up a proportion based on the similar triangles: 7 / 9 = 14 / x. Solving this equation leads to x = 18.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, one with legs of 5 and 8, and the other with legs of 2x and (2x + 6). The problem requires setting up a proportion: 5 / 8 = 2x / (2x + 6). Solving this equation leads to x = 5, which then allows us to find the side lengths of 10 and 16.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°). Two triangles are shown, with the smaller one having sides of 6√3 and 6, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: (6√3) / 6 = x / 12. Solving this equation leads to x = 12√3.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°) and algebraic expressions. Two triangles are shown, with the smaller one having sides of 16 and 8, and the larger one having sides of (3x + 4) and 2x. The problem requires setting up a proportion: 16 / 8 = (3x + 4) / 2x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 8 and 16.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the smaller one having sides of 4 and 3, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: 4 / 3 = x / 12. Solving this equation leads to x = 16.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the smaller one having sides of (3x + 4) and 6, and the larger one having sides of 3x and 3x. The problem requires setting up a proportion: 8 / 6 = (3x + 4) / 3x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 12 and 16.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 12 / 5 = x / 15. Solving this equation leads to x = 36.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of 10x + 8 and 5x. The problem requires setting up a proportion: 12 / 5 = (10x + 8) / 5x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 20 and 48.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar isosceles right triangles. Two 45-45-90 triangles are shown, with one having sides labeled y and 5√2, and the other having sides labeled x and 12. The problem requires finding the lengths of both x and y using the special properties of isosceles right triangles and proportions.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion where b is expressed as x + 1, and c and d are given constants (c = 3, d = 2). The goal is to solve for a using the proportion a / b = c / d. By substituting the known values, we set up the equation a / (x + 1) = 3 / 2 and solve for a, resulting in the expression a = (3(x + 1)) / 2.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar isosceles right triangles with algebraic expressions. Two 45-45-90 triangles are shown, with one having sides labeled 15√2 and 15, and the other having sides labeled √2 * 5x and y. The problem requires finding the length of y in terms of x using the special properties of isosceles right triangles and proportions.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar isosceles triangles. Two isosceles triangles are shown, with the smaller one having sides of 30 and 16, and the larger one having sides of x and 20. The problem requires finding the length of side x by setting up a proportion: 30 / 16 = x / 20. Solving this equation leads to x = 37.5.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar isosceles triangles with algebraic expressions. Two isosceles triangles are shown, with the smaller one having sides of 22 and 12, and the larger one having sides of 10x + 5 and 6x. The problem requires setting up a proportion: 22 / 12 = (10x + 5) / 6x. Solving this equation leads to x = 5, which then allows us to find the side lengths of the larger triangle.

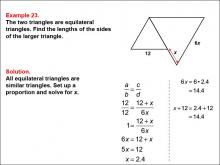
Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar equilateral triangles. Two equilateral triangles are shown, with the smaller one having a side length of 12, and the larger one having a side length of 6x and an additional side labeled as 12 + x. The problem requires finding the lengths of the sides of the larger triangle by setting up a proportion: 12 / 12 = (12 + x) / 6x. Solving this equation leads to x = 2.4, and the length of the larger triangle's side is found to be approximately 14.4 units.

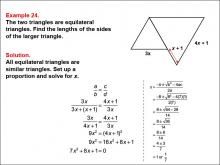
Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a complex proportion problem using similar equilateral triangles with algebraic expressions. Two equilateral triangles are shown, with the smaller one having a side length of 3x, and the larger one having side lengths labeled as (4x + 1) and (x + 1). The problem requires setting up a proportion: 3x / (4x + 1) = 3x / (3x + (x + 1)). Solving this equation leads to a quadratic equation, which when solved gives x ≈ 7/1.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar rectangles. Two rectangles are shown, with the smaller one having sides of 2 and 3, and the larger one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 2 / 3 = x / 15. Solving this equation leads to x = 10.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar rectangles with algebraic expressions. Two rectangles are shown, with the smaller one having sides of 5 and 12, and the larger one having sides of x + 5 and 3x + 6. The problem requires setting up a proportion: 5 / 12 = (x + 5) / (3x + 6). Solving this equation leads to x = 10, which then allows us to find the side lengths of the larger rectangle as 15 and 36.

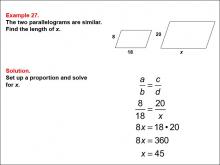
Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar parallelograms. Two parallelograms are shown, with the smaller one having sides of 8 and 18, and the larger one having sides of 20 and x. The problem requires finding the length of side x by setting up a proportion: 8 / 18 = 20 / x. Solving this equation leads to x = 45.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar parallelograms with algebraic expressions. Two parallelograms are shown, with the smaller one having sides of 9 and 21, and the larger one having sides of x + 12 and 4x + 3. The problem requires setting up a proportion: 9 / 21 = (x + 12) / (4x + 3). Solving this equation leads to x = 15, which then allows us to find the side lengths of the larger parallelogram as 27 and 63.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two triangles are similar using proportions. Two triangles are shown, both with a 70° angle. The first triangle has sides of 12 and 10, while the second has sides of 18 and 15. The problem requires setting up a proportion to check for similarity: 12 / 10 = 18 / 15. After simplifying, both ratios are equal (6 / 5 = 6 / 5), confirming that the triangles are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving for b in a proportion where a = 8, c = 4, and d = 3. We set up the proportion 8 / b = 4 / 3 and solve for b, resulting in b = 6. This problem shows how to find an unknown value in the denominator of a proportion.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates how to determine if two triangles are not similar using proportions. Two triangles are shown, both with a 75° angle. The first triangle has sides of 15 and 9, while the second has sides of 28 and 18. The problem requires setting up a proportion to check for similarity: 15 / 9 = 28 / 18. After simplifying, the ratios are not equal (5 / 3 ≠ 14 / 9), concluding that the triangles are not similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two right triangles are similar using proportions. Two right triangles are shown, one with legs of length 4 and 3, and the other with legs of length 10 and 7.5. The problem requires setting up a proportion to check for similarity: 4 / 3 = 10 / 7.5. After simplifying, both ratios are equal (4 / 3 = 4 / 3), confirming that the triangles are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates how to determine if two right triangles are not similar using proportions. Two right triangles are shown, one with legs of length 12 and 5, and the other with legs of length 35 and 15. The problem requires setting up a proportion to check for similarity: 12 / 5 = 35 / 15. After simplifying, the ratios are not equal (12 / 5 ≠ 7 / 3), concluding that the triangles are not similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two rectangles are similar using proportions. Two rectangles are shown, with the first having dimensions 3 and 8, and the second having dimensions 9 and 24. The problem requires setting up a proportion to check for similarity: 3 / 8 = 9 / 24. After simplifying, the ratios are equal, confirming that the rectangles are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates how to determine if two rectangles are similar using proportions with algebraic expressions. Two rectangles are shown, with the first having dimensions 11.5 and 23, and the second having dimensions 23x and 46x. The problem requires setting up a proportion to check for similarity: 11.5 / 23 = 23x / 46x. After simplifying, the ratios are equal, confirming that the rectangles are indeed similar for any value of x.