Illustrative Math Alignment: Grade 6 Unit 1

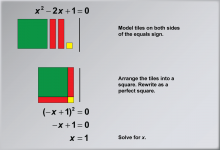
Topic

Solving Equations

Description

In this example, we explore solving the quadratic equation x2 - 2x + 1 = 0 using algebra tiles. The visual representation demonstrates how to arrange the tiles into a perfect square, effectively transforming the equation into (-x + 1)2 = 0. This method showcases the versatility of algebra tiles in handling equations with both positive and negative terms, as well as illustrating the completing the square technique.

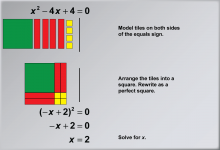
Topic

Solving Equations

Description

This example demonstrates the process of solving the quadratic equation x2 - 4x + 4 = 0 using algebra tiles. The visual representation shows how to arrange the tiles to form a perfect square, illustrating the completing the square method. By organizing the tiles, students can physically see how the terms combine to form the expression (-x + 2)2 = 0, making the solution process more intuitive and accessible.

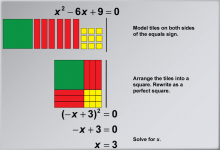
Topic

Solving Equations

Description

This example illustrates the process of solving the quadratic equation x2 - 6x + 9 = 0 using algebra tiles. By modeling tiles on both sides of the equation, students can visually understand the principle of maintaining equality while manipulating the equation. The tiles are arranged into a square to form a perfect square trinomial, demonstrating the completing the square method in a tangible way.

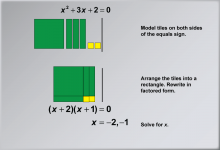
Topic

Solving Equations

Description

This example demonstrates the process of solving the quadratic equation x2 + 3x + 2 = 0 using algebra tiles. The visual representation shows how to arrange the tiles into a rectangle, illustrating the factoring method for solving quadratic equations. By organizing the tiles in this way, students can physically see how the terms combine to form the factored expression (x + 2)(x + 1) = 0, making the solution process more intuitive and accessible.

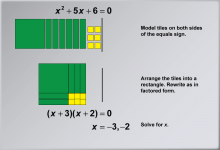
Topic

Solving Equations

Description

This example illustrates the process of solving the quadratic equation x2 + 5x + 6 = 0 using algebra tiles. The visual representation demonstrates how to arrange the tiles into a rectangle, showcasing the factoring method for solving quadratic equations. By organizing the tiles in this manner, students can physically see how the terms combine to form the factored expression (x + 3)(x + 2) = 0, making the solution process more concrete and understandable.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and addition demonstrates solving the equation 2x + 3 = 7 by performing two inverse operations to isolate x. The operations shown are subtracting 3 from both sides and then dividing by 2. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and addition involves solving -3x + (-12) = -42 by performing two inverse operations: addition and division to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and addition shows solving the equation 3x + 4 = 13 by using two inverse operations. The steps involve subtracting 4 and then dividing by 3. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and addition involves solving the equation 2x + 4 = 8 using inverse operations. It shows subtraction and division to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and addition illustrates solving -4x + 5 = 25. It uses inverse operations by subtracting 5 and dividing by -4. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and addition shows the solution to -7x + 6 = 48 by isolating x with inverse operations, including subtraction and division. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and addition solves the equation 6x + (-2) = 34 by using inverse operations, specifically addition and division, to find the value of x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and addition solves 10x + (-6) = 54 by isolating x through inverse operations, including addition and division. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and addition shows solving -x + (-5) = 71 by performing inverse operations to isolate x, using addition and division by -1. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and addition demonstrates solving -2x + (-8) = 22 through inverse operations, specifically addition and division, to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and subtraction shows solving the equation 2x - 3 = 7 by isolating x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and subtraction demonstrates solving the equation -3x - (-12) = -42 by isolating x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and subtraction illustrates solving the equation 3x - 4 = 14 by isolating x with inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and subtraction demonstrates solving the equation -2x - 4 = 8 by isolating x using inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and subtraction explains solving the equation -x - 5 = 17 by isolating x with inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and subtraction shows solving the equation -7x - 6 = 43 by isolating x with inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and subtraction illustrates solving the equation 6x - (-2) = 38 by isolating x using inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and subtraction demonstrates solving the equation 10x - (-6) = 76 by isolating x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and subtraction explains solving the equation -x - (-5) = 71 by isolating x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation involving multiplication and subtraction shows solving the equation -2x - (-8) = 22 by isolating x with inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and addition: x/5 + 3 = 7. The solution is detailed with inverse operations to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and addition: -x/3 + (-12) = -42. The solution follows each step using inverse operations to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and addition: x/4 + 4 = 14. It includes each step to isolate the variable using inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and addition: -x/3 + 4 = 8. The solution uses inverse operations to isolate x with careful handling of the negative sign. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and addition: -x/6 + 5 = 17. The solution details each inverse operation step to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and addition: -x/7 + 6 = 43. The solution carefully applies inverse operations to solve for x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and addition: x/6 + (-2) = 38, showing each step to isolate x through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and addition: x/10 + (-6) = 76. Each inverse operation is shown to solve for x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and addition: -x/9 + (-5) = 71. The solution includes each inverse operation needed to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and addition: -x/2 + (-8) = 22, detailing the inverse operations step-by-step to solve for x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and subtraction: x / 5 - 3 = 7 using two inverse operations to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and subtraction: -x / 3 - (-12) = -42 with two inverse operations to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and subtraction: x / 4 - 4 = 14 with a two-step inverse operation approach. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and subtraction: -x / 3 - 4 = 8 through inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and subtraction: -x / 6 - 5 = 17 using two inverse operations to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and subtraction: -x / 7 - 6 = 43 using inverse operations to isolate the variable. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and subtraction: x / 6 - (-2) = 38 with a two-step approach using inverse operations. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and subtraction: x / 10 - (-6) = 76 by performing two inverse operations to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and subtraction: -x / 9 - (-5) = 71 using two inverse operations to isolate the variable. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

An example of solving a two-step equation with division and subtraction: -x / 2 - (-8) = 22 by performing two inverse operations to isolate x. This example demonstrates how to isolate the variable by first undoing any addition or subtraction, followed by division to find the solution.

Solving equations is a foundational skill in algebra, involving steps to isolate the variable and solve for its value. This collection of examples illustrates different methods for solving two-step equations, reinforcing the importance of order in arithmetic operations.

Topic

Solving Equations

Description

This example effectively demonstrates solving a two-step equation using algebra tiles, where the visual model helps students understand how to manipulate the equation. The image depicts solving 2x + 2 = 4 using algebra tiles, showing steps including modeling, creating zero pairs, and dividing to find x. In this example, the caption emphasizes the importance of using model tiles to visualize the equation.

Topic

Solving Equations

Description

This example effectively demonstrates solving a two-step equation using algebra tiles, where the visual model helps students understand how to manipulate the equation. The image illustrates solving the equation -2x - 1 = 5 with algebra tiles. It shows steps: modeling both sides, turning subtraction into addition of a negative, creating zero pairs, and replacing with opposite tiles to solve for x = -3. This process combines multiple concepts seen in previous examples.

Topic

Solving Equations

Description

This example effectively demonstrates solving a two-step equation using algebra tiles, where the visual model helps students understand how to manipulate the equation. The image illustrates the equation 2x + 1 = 5 with algebra tiles. It shows how to solve for x by modeling, adding opposite tiles, and dividing the remaining tiles. In this example, the caption emphasizes the importance of using model tiles to visualize the equation.

Topic

Solving Equations

Description

This example effectively demonstrates solving a two-step equation using algebra tiles, where the visual model helps students understand how to manipulate the equation. The image shows a visual representation of the equation 3x + 1 = 4 using algebra tiles. It demonstrates the steps to solve for x by modeling, creating zero pairs, and dividing. In this example, the caption emphasizes the importance of using model tiles to visualize the equation.

Topic

Solving Equations

Description

This example effectively demonstrates solving a two-step equation using algebra tiles, where the visual model helps students understand how to manipulate the equation. This image represents solving 2x - 2 = 4 with algebra tiles, converting subtraction into addition of negatives, and solving for x through zero pairs and division. In this example, the caption emphasizes the importance of using model tiles to visualize the equation.