
Illustrative Math Alignment: Grade 6 Unit 1
Expressions and Equations
Lesson 4: Practice Solving Equations and Representing Situations with Equations
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Example: Solving Two-Step Equations with Algebra Tiles--Example 5 | Math Example: Solving Two-Step Equations with Algebra Tiles--Example 5TopicSolving Equations DescriptionThis example effectively demonstrates solving a two-step equation using algebra tiles, where the visual model helps students understand how to manipulate the equation. The image shows algebra tiles used to solve the equation 2x - 2 = -4. The tiles are manipulated to find the solution x = -1. In this example, the caption emphasizes the importance of using model tiles to visualize the equation. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations with Algebra Tiles--Example 6 | Math Example: Solving Two-Step Equations with Algebra Tiles--Example 6TopicSolving Equations DescriptionThis example effectively demonstrates solving a two-step equation using algebra tiles, where the visual model helps students understand how to manipulate the equation. The image shows algebra tiles used to solve the equation 2x - (-2) = -4. The tiles are manipulated to find the solution x = -3. In this example, the process involves modeling tiles on both sides of the equals sign, converting subtraction of a negative into addition, and creating zero pairs to isolate the variable. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations with Algebra Tiles--Example 7 | Math Example: Solving Two-Step Equations with Algebra Tiles--Example 7TopicSolving Equations DescriptionThis example effectively demonstrates solving a two-step equation using algebra tiles, where the visual model helps students understand how to manipulate the equation. The image shows algebra tiles used to solve the equation -x + 1 = 4. The tiles are manipulated to find the solution x = -3. In this example, the process involves modeling tiles on both sides of the equals sign, creating zero pairs, and replacing each side with corresponding opposite tiles. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations with Algebra Tiles--Example 8 | Math Example: Solving Two-Step Equations with Algebra Tiles--Example 8TopicSolving Equations DescriptionThis example effectively demonstrates solving a two-step equation using algebra tiles, where the visual model helps students understand how to manipulate the equation. The image shows algebra tiles used to solve the equation -x - 1 = 4. The tiles are manipulated to find the solution x = -5. In this example, the process involves modeling tiles on both sides of the equals sign, converting subtraction into addition of a negative, creating zero pairs, and replacing each side with corresponding opposite tiles. |
Solving Two-Step Equations |

|
Math Example: Solving Two-Step Equations with Algebra Tiles--Example 9 | Math Example: Solving Two-Step Equations with Algebra Tiles--Example 9TopicSolving Equations DescriptionThis example effectively demonstrates solving a two-step equation using algebra tiles, where the visual model helps students understand how to manipulate the equation. The image shows a visual representation of solving the equation -2x + 1 = 5 using algebra tiles. The tiles are arranged to show steps: modeling both sides, creating zero pairs, and replacing with opposite tiles to solve for x = -2. This process illustrates the importance of maintaining balance in equations. |
Solving Two-Step Equations |

|
MATH EXAMPLES--Teacher's Guide: Solving Equations with Fractions | MATH EXAMPLES--Teacher's Guide: Solving Equations with Fractions
This Teacher's Guide provides an overview of the 13 worked-out examples that solve a variety of one-variable equations with fractions. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Solving Fraction Equations |

|
MATH EXAMPLES--Teacher's Guide: Solving Equations with Percents | MATH EXAMPLES--Teacher's Guide: Solving Equations with Percents
What Are Percents?Percents Are a Type of Fraction |
Solving Percent Equations |

|
MATH EXAMPLES--Teacher's Guide: Solving One-Variable Equations | MATH EXAMPLES--Teacher's Guide: Solving One-Variable Equations
This Teacher's Guide provides an overview of the 27 worked-out examples that solve a variety of one-variable equations. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Equations and Inequalities |

|
MATH EXAMPLES--The Discriminant | MATH EXAMPLES--The Discriminant
This set of tutorials provides 10 examples of finding the determinant of a quadratic equation to determine the number of real roots. NOTE: The download is a PPT file. |
Quadratic Equations and Functions and Quadratic Formula |

|
Math in the News: Issue 92--How Netflix Is Changing Media | Math in the News: Issue 92--How Netflix Is Changing Media
February 2014. In this issue of Math in the News we look at the dramatic growth in subscribers for Netflix. We calculate the rate of growth. We also explore how companies like Netflix are changing the viewing habits of all Americans. This is part of the Math in the News collection. To see the complete collection, click on this link. Note: The download is a PPT file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Exponential and Logarithmic Functions |

|
Paper-and-Pencil Quiz: Equations with Fractions (Easy) | Paper-and-Pencil Quiz: Equations with Fractions (Easy)
This is part of a collection of math quizzes on the topic of Equations with Fractions. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Solving Fraction Equations |

|
Paper-and-Pencil Quiz: Equations with Fractions (Hard) | Paper-and-Pencil Quiz: Equations with Fractions (Hard)
This is part of a collection of math quizzes on the topic of Equations with Fractions. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Solving Fraction Equations |

|
Paper-and-Pencil Quiz: Equations with Fractions (Medium) | Paper-and-Pencil Quiz: Equations with Fractions (Medium)
This is part of a collection of math quizzes on the topic of Equations with Fractions. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Solving Fraction Equations |

|
Paper-and-Pencil Quiz: Equations with Percents (Easy) | Paper-and-Pencil Quiz: Equations with Percents (Easy)
This is part of a collection of math quizzes on the topic of Equations with Percents. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Solving Percent Equations |

|
Paper-and-Pencil Quiz: Equations with Percents (Hard) | Paper-and-Pencil Quiz: Equations with Percents (Hard)
This is part of a collection of math quizzes on the topic of Equations with Percents. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Solving Percent Equations |

|
Paper-and-Pencil Quiz: Equations with Percents (Medium) | Paper-and-Pencil Quiz: Equations with Percents (Medium)
This is part of a collection of math quizzes on the topic of Equations with Percents. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Solving Percent Equations |

|
Video Definition 1--Equation Concepts--"Not Equal To" Sign | Video Definition 1--Equation Concepts--"Not Equal To" Sign
TopicEquations DescriptionThe Not Equal To Sign (≠) indicates two expressions are not equal, forming an inequation. For example, 2 + 1 ≠ 4 and x + 3 ≠ x are inequations. This term builds on equality concepts by introducing inequalities, critical for exploring a broader range of mathematical statements. |
Numerical and Algebraic Expressions |

|
Video Definition 10--Equation Concepts--Equation | Video Definition 10--Equation Concepts--Equation
TopicEquations DescriptionAn Equation is a mathematical statement that says two expressions are equal to each other. Equations can be true or false, as shown in examples like 1 + 1 = 2 (true) and 1 + 2 = 4 (false). This term introduces the concept of equality and sets the foundation for understanding other types of equations. |
Applications of Equations and Inequalities |

|
Video Definition 11--Equation Concepts--Equations in One Variable | Video Definition 11--Equation Concepts--Equations in One Variable
TopicEquations DescriptionAn Equation in One Variable has an unknown represented by a single variable. Examples include 2 + 3x = 5 and (x + 2)^2 = 25. This term focuses on single-variable equations, forming a basis for solving and understanding algebraic structures. |
Applications of Equations and Inequalities |

|
Video Definition 12--Equation Concepts--Equations in Two Variables | Video Definition 12--Equation Concepts--Equations in Two Variables
TopicEquations DescriptionEquations in Two Variables. A two-variable equation shows a relationship between two variables. Examples include y = 3x + 5, x2 + y2 = 25, and xy = 5, highlighting equations that can be graphed in a coordinate system. This builds on the idea of variables in equations and introduces the concept of relationships between variables, applicable in graphing and real-world modeling. |
Applications of Equations and Inequalities |

|
Video Definition 13--Equation Concepts--Equivalent Equations | Video Definition 13--Equation Concepts--Equivalent Equations
TopicEquations DescriptionEquivalent Equations result from changing an equation while maintaining equality, often by performing the same operation on both sides. For example, x - 3 = 5 becomes x = 8 after adding 3 to both sides. This term demonstrates how equations can be manipulated without altering their solution, a key concept in solving equations. |
Applications of Equations and Inequalities |

|
Video Definition 14--Equation Concepts--False Equation | Video Definition 14--Equation Concepts--False Equation
TopicEquations DescriptionA False Equation is mathematically inaccurate. For example, 2 + 1 = 4 is false, and x + 3 = x has no solution, as no value of x satisfies the equation. This term contrasts true equations and emphasizes the need to verify solutions, highlighting logical consistency in mathematics. |
Applications of Equations and Inequalities |

|
Video Definition 15--Equation Concepts--Identity Equation | Video Definition 15--Equation Concepts--Identity Equation
TopicEquations DescriptionAn Identity Equation is always true for all variable values. Examples include x = x and (x + 1)2 = x2 + 2x + 1. Identity equations often use the symbol ≡ to indicate their universal truth. This term introduces a special class of equations, linking algebraic manipulation and properties of equivalence. |
Applications of Equations and Inequalities |

|
Video Definition 16--Equation Concepts--Inequation | Video Definition 16--Equation Concepts--Inequation
TopicEquations DescriptionAn Inequation is a mathematical statement that shows two expressions are not equal, as in 2 + 1 ≠ 4 or x + 3 ≥ 0, which includes inequalities. This term broadens the discussion to include inequalities, expanding the types of relationships between expressions. |
Inequalities |

|
Video Definition 17--Equation Concepts--Isolating the Variable | Video Definition 17--Equation Concepts--Isolating the Variable
TopicEquations DescriptionIsolating the Variable refers to the process of solving an equation by focusing on and isolating the variable of interest. For example, x + 3 = 5 becomes x = 2 by subtracting 3 from both sides. This term highlights a key step in solving equations, emphasizing strategies for simplifying equations to find solutions. |
Variables and Unknowns |

|
Video Definition 18--Equation Concepts--Left Side of the Equation | Video Definition 18--Equation Concepts--Left Side of the Equation
TopicEquations DescriptionThe Left Side of the Equation is the expression on the left of the equals sign. For example, in 2x + 3 = x - 5, the left side is 2x + 3. This term provides clarity in identifying components of equations, aiding in understanding structure and solving strategies. |
Applications of Equations and Inequalities |

|
Video Definition 19--Equation Concepts--Linear Equation | Video Definition 19--Equation Concepts--Linear Equation
TopicEquations DescriptionA Linear Equation is an equation where variables have an exponent of 1. Examples include x + 2 = 7, 2x + 3y = 4, and y = -2x + 10. Graphs of two-variable linear equations are straight lines. This term introduces a fundamental class of equations with specific properties, crucial for algebra and graphing. |
Applications of Linear Functions |

|
Video Definition 2--Equation Concepts--Addition Property of Equality | Video Definition 2--Equation Concepts--Addition Property of Equality
TopicEquations DescriptionThe Addition Property of Equality allows the addition of the same quantity to each side of an equation while maintaining equality. For example, if a = b, then a + c = b + c. This concept ensures equations can be manipulated while preserving their equality, demonstrated by solving x - 2 = 3 as x = 5 after adding 2 to both sides. This term introduces the basic manipulation of equations, forming the foundation for solving linear equations and maintaining equality. |
Applications of Equations and Inequalities |

|
Video Definition 20--Equation Concepts--Literal Equation | Video Definition 20--Equation Concepts--Literal Equation
TopicEquations DescriptionA Literal Equation includes more than one variable and often represents formulas, such as A = πr2, V = l*w*h, and SA = 2πr*h + 2πr2. This term connects to real-world applications and highlights the versatility of equations in representing formulas and relationships. |
Applications of Equations and Inequalities |

|
Video Definition 21--Equation Concepts--Multi-Step Equation | Video Definition 21--Equation Concepts--Multi-Step Equation
TopicEquations DescriptionA Multi-Step Equation involves more than two mathematical operations to solve. For example, 4x + 2 = 2x + 8 simplifies to x = 3 after subtraction and division steps. This term emphasizes solving more complex equations, showing sequential steps and reinforcing logical progression in algebra. |
Solving Multistep Equations |

|
Video Definition 22--Equation Concepts--Multiplication Property of Equality | Video Definition 22--Equation Concepts--Multiplication Property of Equality
TopicEquations DescriptionThe Multiplication Property of Equality allows multiplication by the same non-zero quantity on both sides of an equation, maintaining equality. For example, if a = b, then a * c = b * c. Solving x/2 = 3 yields x = 6 by multiplying both sides by 2. This term builds on equality principles and demonstrates another method for solving equations by manipulating terms. |
Applications of Equations and Inequalities |

|
Video Definition 23--Equation Concepts--Nonlinear Equation | Video Definition 23--Equation Concepts--Nonlinear Equation
TopicEquations DescriptionA Non-Linear Equation includes non-linear terms such as polynomials of degree 2 or higher, exponential, logarithmic, or trigonometric terms. Examples include y = x2 - 4x + 5 and y = sin(x). This term expands understanding beyond linear relationships, introducing diverse mathematical models and their applications. |
Applications of Equations and Inequalities |

|
Video Definition 24--Equation Concepts--Numerical Expression | Video Definition 24--Equation Concepts--Numerical Expression
TopicEquations DescriptionA Numerical Expression consists of numbers and operations without variables. Examples include 2 + 3 = 5 and 2(4 + 3) = 14. This term highlights fundamental operations, foundational for understanding and solving equations. The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Numerical Expressions |

|
Video Definition 25--Equation Concepts--One-Step Equation | Video Definition 25--Equation Concepts--One-Step Equation
TopicEquations DescriptionA One-Step Equation involves a single mathematical operation to solve. For example, x + 2 = 3 simplifies to x = 1 by subtraction. This term introduces the simplest form of equations, essential for beginners to build confidence and understanding in solving. |
Solving One-Step Equations |

|
Video Definition 26--Equation Concepts--Polynomial Equation | Video Definition 26--Equation Concepts--Polynomial Equation
TopicEquations DescriptionA Polynomial Equation consists of a polynomial expression equal to zero. Examples include x2 + 3x + 2 = 0 and x3 - 2x2 + 4x - 10 = 0. This term defines a key class of equations, critical for algebra and calculus studies. |
Polynomial Functions and Equations |

|
Video Definition 27--Equation Concepts--Quadratic Equation | Video Definition 27--Equation Concepts--Quadratic Equation
TopicEquations DescriptionA Quadratic Equation is a polynomial of degree 2. Examples include x2 - 2 = 23 and 2x2 + 3x + 2 = 0. Graphs of such equations are parabolas. This term extends understanding of polynomial equations, connecting algebra to geometry through parabolas. |
Quadratic Equations and Functions |

|
Video Definition 28--Equation Concepts--Reflexive Property of Equality | Video Definition 28--Equation Concepts--Reflexive Property of Equality
TopicEquations DescriptionThe Reflexive Property of Equality states that any quantity is equal to itself. Examples include 5 = 5 and x + 2 = x + 2. This term reinforces the foundational principle of equality, essential for logical reasoning in mathematics. |
Applications of Equations and Inequalities |

|
Video Definition 29--Equation Concepts--Right Side of the Equation | Video Definition 29--Equation Concepts--Right Side of the Equation
TopicEquations DescriptionRight Side of the Equation. The expression to the right side of the equals sign in an equation. 2x + 3 = x - 5 (right side highlighted) The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 3--Equation Concepts--Algebraic Equation | Video Definition 3--Equation Concepts--Algebraic Equation
TopicEquations DescriptionAn Algebraic Equation is another term for a polynomial equation, represented as a sum of terms equal to zero. Examples include x2 + 3x + 2 = 0 and x3 - 2x2 + 4x - 10 = 0. It highlights the structure of polynomial equations using constants, variables, and powers. This term connects to the topic by defining the types of equations learners encounter when solving or simplifying expressions. |
Applications of Equations and Inequalities |
|
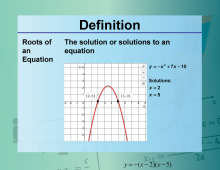
Video Definition 30--Equation Concepts--Roots of an Equation | Video Definition 30--Equation Concepts--Roots of an Equation
TopicEquations DescriptionRoots of an Equation. The solution or solutions to an equation. y = -x2 + 7x - 10; solutions: x = 2, x = 5 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 31--Equation Concepts--Solution | Video Definition 31--Equation Concepts--Solution
TopicEquations DescriptionSolution. A value for the unknown that turns a conditional equation into a true equation. For example, x = 5 is a solution to x + 2 = 7 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 32--Equation Concepts--Solving an Equation | Video Definition 32--Equation Concepts--Solving an Equation
TopicEquations DescriptionSolving an Equation. The process of finding the value(s) for a variable that result in a true equation. For example, x + 2 = 3 has a solution of x = 1 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 33--Equation Concepts--Subtraction Property of Equality | Video Definition 33--Equation Concepts--Subtraction Property of Equality
TopicEquations DescriptionSubtraction Property of Equality. The property that allows the subtraction of the same quantity from each side of an equation while maintaining the equality. For example, x + 2 = 3 becomes x = 1 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 34--Equation Concepts--Symmetric Property of Equality | Video Definition 34--Equation Concepts--Symmetric Property of Equality
TopicEquations DescriptionSymmetric Property of Equality. The property that states that an equation can be written two ways, with both sides interchanged. If a = b, then b = a. The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 35--Equation Concepts--The Unknown | Video Definition 35--Equation Concepts--The Unknown
TopicEquations DescriptionThe Unknown. In a conditional equation, the variable is also referred to as the unknown. 3x = 12, where x is the unknown The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Variables and Unknowns |

|
Video Definition 36--Equation Concepts--Transitive Property of Equality | Video Definition 36--Equation Concepts--Transitive Property of Equality
TopicEquations DescriptionTransitive Property of Equality. The property that states that two quantities equal to a third quantity are equal to each other. If a = b and b = c, then a = c The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 37--Equation Concepts--True Equation | Video Definition 37--Equation Concepts--True Equation
TopicEquations DescriptionTrue Equation. A mathematically accurate equation. If variables are involved, the true equation is for the values of the variable that make the equation true. Examples: 2 + 1 = 3; (2 + 3)2 = 25; x + 3 = 9 for x = 6 The topic of this video is closely tied to Equations, providing an essential understanding of its fundamental concepts. This video explores the mathematics behind this topic by delving into how key principles are applied in practical contexts. |
Applications of Equations and Inequalities |

|
Video Definition 38--Equation Concepts--Two-Step Equation | Video Definition 38--Equation Concepts--Two-Step Equation
TopicEquations DescriptionTwo-Step Equation. A two-step equation is an equation that involves two mathematical operations to solve. The example given is 2x + 2 = 8, where the first operation is subtraction, leading to 2x = 6, followed by division to solve for x = 3. This concept extends the understanding of solving equations by introducing a sequence of operations, crucial for solving more complex equations. |
Solving Two-Step Equations |

|
Video Definition 39--Equation Concepts--Variable Expression | Video Definition 39--Equation Concepts--Variable Expression
TopicEquations DescriptionVariable Expression. A variable expression is made up of numbers, operations, and variables. Examples include 2x + 3 = 5 (expression on the left), 4 = 3x + 7 (expression on the right), and 4x + 3 = x - 5 (expressions on both sides). This connects variables to equations and highlights their role in forming relationships within mathematical contexts. |
Variable Expressions |

|
Video Definition 4--Equation Concepts--Algebraic Expression | Video Definition 4--Equation Concepts--Algebraic Expression
TopicEquations DescriptionAn Algebraic Expression consists of numbers, operations, and variables. Unlike equations, expressions may not have an equality. Examples include 2x + 3, 4 = 3x + 7, and 4x + 3 = x - 5, demonstrating their versatility in representing mathematical relationships. This term distinguishes between expressions and equations, forming the basis for manipulating algebraic forms before solving equations. |
Numerical and Algebraic Expressions |