Illustrative Math-Media4Math Alignment

 

 

Illustrative Math Alignment: Grade 6 Unit 9

Putting it All Together

Lesson 4: How Do We Choose?

Use the following Media4Math resources with this Illustrative Math lesson.

Thumbnail Image Title Body Curriculum Topics
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 2 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 2 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 2

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 3 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 3 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 3

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 4 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 4 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 4

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 5 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 5 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 5

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 6 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 6 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 6

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 7 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 7 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 7

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 8 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 8 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 8

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 9 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 9 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 9

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 10 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 10 Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 10

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
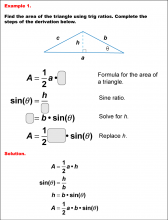
Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 1 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 1 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 1

This is part of a collection of math examples that show how to area and perimeter for different geometric shapes.

 Trig Expressions and Identities
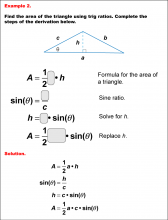
Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 2 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 2 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 2

This is part of a collection of math examples that show how to area and perimeter for different geometric shapes.

 Trig Expressions and Identities
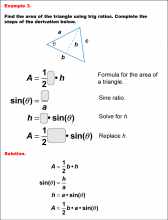
Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 3 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 3 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 3

This is part of a collection of math examples that show how to area and perimeter for different geometric shapes.

 Trig Expressions and Identities
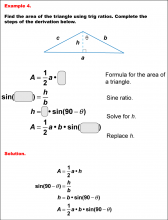
Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 4 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 4 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 4

This is part of a collection of math examples that show how to area and perimeter for different geometric shapes.

 Trig Expressions and Identities
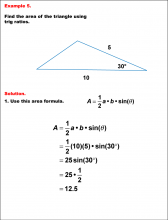
Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 5 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 5 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 5

This is part of a collection of math examples that show how to area and perimeter for different geometric shapes.

 Trig Expressions and Identities
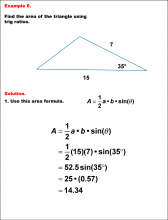
Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 6 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 6 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 6

This is part of a collection of math examples that show how to area and perimeter for different geometric shapes.

 Trig Expressions and Identities
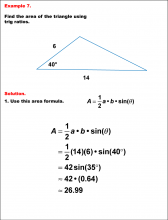
Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 7 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 7 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 7

This is part of a collection of math examples that show how to area and perimeter for different geometric shapes.

 Trig Expressions and Identities
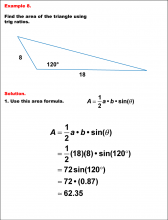
Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 8 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 8 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 8

This is part of a collection of math examples that show how to area and perimeter for different geometric shapes.

 Trig Expressions and Identities
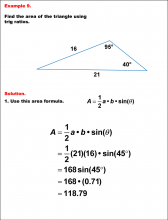
Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 9 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 9 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 9

This is part of a collection of math examples that show how to area and perimeter for different geometric shapes.

 Trig Expressions and Identities
Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 10 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 10 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 10

This is part of a collection of math examples that show how to area and perimeter for different geometric shapes.

 Trig Expressions and Identities
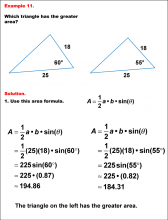
Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 11 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 11 Math Example--Area and Perimeter--Triangular Area Using Trig Ratios: Example 11

This is part of a collection of math examples that show how to area and perimeter for different geometric shapes.

 Trig Expressions and Identities
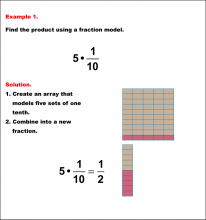
Math Example: Fraction Operations--Multiplying Fractions and Whole Numbers Using Models: Example 1 Math Example: Fraction Operations--Multiplying Fractions and Whole Numbers Using Models: Example 1 Multiplying Fractions and Whole Numbers Using Models: Example 1

Topic

Fraction Operations

 Fractions and Mixed Numbers
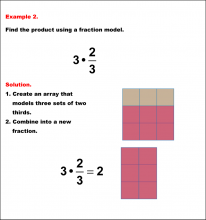
Math Example: Fraction Operations--Multiplying Fractions and Whole Numbers Using Models: Example 2 Math Example: Fraction Operations--Multiplying Fractions and Whole Numbers Using Models: Example 2 Multiplying Fractions and Whole Numbers Using Models: Example 2

Topic

Fraction Operations

 Fractions and Mixed Numbers
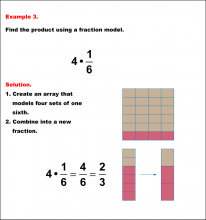
Math Example: Fraction Operations--Multiplying Fractions and Whole Numbers Using Models: Example 3 Math Example: Fraction Operations--Multiplying Fractions and Whole Numbers Using Models: Example 3 Multiplying Fractions and Whole Numbers Using Models: Example 3

Topic

Fraction Operations

 Fractions and Mixed Numbers
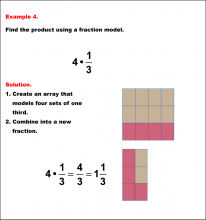
Math Example: Fraction Operations--Multiplying Fractions and Whole Numbers Using Models: Example 4 Math Example: Fraction Operations--Multiplying Fractions and Whole Numbers Using Models: Example 4 Multiplying Fractions and Whole Numbers Using Models: Example 4

Topic

Fraction Operations

 Fractions and Mixed Numbers
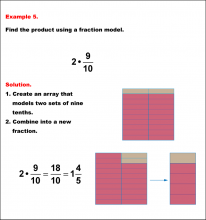
Math Example: Fraction Operations--Multiplying Fractions and Whole Numbers Using Models: Example 5 Math Example: Fraction Operations--Multiplying Fractions and Whole Numbers Using Models: Example 5 Math Example: Fraction Operations--Multiplying Fractions and Whole Numbers Using Models: Example 5

Topic

Fraction Operations

 Fractions and Mixed Numbers
Math Example--Rational Concepts--Rational vs Irrational--Example 5 Math Example--Rational Concepts--Rational vs Irrational--Example 5 Math Example--Rational Concepts--Rational vs Irrational--Example 5

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational vs Irrational--Example 6 Math Example--Rational Concepts--Rational vs Irrational--Example 6 Math Example--Rational Concepts--Rational vs Irrational--Example 6

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational vs Irrational--Example 7 Math Example--Rational Concepts--Rational vs Irrational--Example 7 Math Example--Rational Concepts--Rational vs Irrational--Example 7

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational vs Irrational--Example 8 Math Example--Rational Concepts--Rational vs Irrational--Example 8 Math Example--Rational Concepts--Rational vs Irrational--Example 8

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational vs Irrational--Example 9 Math Example--Rational Concepts--Rational vs Irrational--Example 9 Math Example--Rational Concepts--Rational vs Irrational--Example 9

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Math Example--Rational Concepts--Rational vs Irrational--Example 10 Math Example--Rational Concepts--Rational vs Irrational--Example 10 Math Example--Rational Concepts--Rational vs Irrational--Example 10

This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.

 Rational Expressions
Definition--Trig Concepts--Trig Ratios Definition--Trig Concepts--Trig Ratios Definition--Trig Concepts--Trig Ratios

This is part of a collection of terms and definitions related to trigonometry concepts.

 Trig Expressions and Identities
Definition--Trig Concepts--Cosine Ratio Definition--Trig Concepts--Cosine Ratio Definition--Trig Concepts--Cosine Ratio

This is part of a collection of terms and definitions related to trigonometry concepts.

 Trig Expressions and Identities
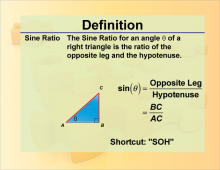
Definition--Trig Concepts--Sine Ratio Definition--Trig Concepts--Sine Ratio Definition--Trig Concepts--Sine Ratio

This is part of a collection of terms and definitions related to trigonometry concepts.

 Trig Expressions and Identities
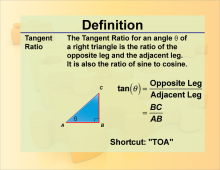
Definition--Trig Concepts--Tangent Ratio Definition--Trig Concepts--Tangent Ratio Definition--Trig Concepts--Tangent Ratio

This is part of a collection of terms and definitions related to trigonometry concepts.

 Trig Expressions and Identities
Definition--Trig Concepts--Secant Ratio Definition--Trig Concepts--Secant Ratio Definition--Trig Concepts--Secant Ratio

This is part of a collection of terms and definitions related to trigonometry concepts.

 Trig Expressions and Identities
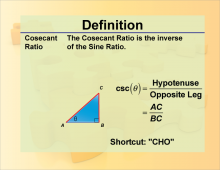
Definition--Trig Concepts--Cosecant Ratio Definition--Trig Concepts--Cosecant Ratio Definition--Trig Concepts--Cosecant Ratio

This is part of a collection of terms and definitions related to trigonometry concepts.

 Trig Expressions and Identities
Definition--Trig Concepts--Cotangent Ratio Definition--Trig Concepts--Cotangent Ratio Definition--Trig Concepts--Cotangent Ratio

This is part of a collection of terms and definitions related to trigonometry concepts.

 Trig Expressions and Identities
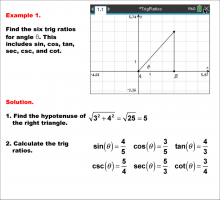
Math Example--Ratios and Rates--Trig Ratios--Example 1 Math Example--Ratios and Rates--Trig Ratios--Example 1 Math Example--Ratios and Rates--Trig Ratios--Example 1

This is part of a collection of math examples that focus on ratios and rates.

 Trig Expressions and Identities
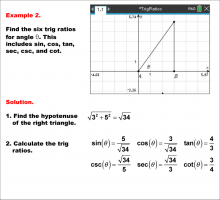
Math Example--Ratios and Rates--Trig Ratios--Example 2 Math Example--Ratios and Rates--Trig Ratios--Example 2 Math Example--Ratios and Rates--Trig Ratios--Example 2

This is part of a collection of math examples that focus on ratios and rates.

 Trig Expressions and Identities
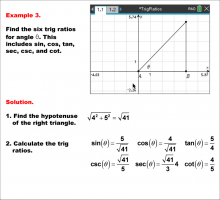
Math Example--Ratios and Rates--Trig Ratios--Example 3 Math Example--Ratios and Rates--Trig Ratios--Example 3 Math Example--Ratios and Rates--Trig Ratios--Example 3

This is part of a collection of math examples that focus on ratios and rates.

 Trig Expressions and Identities
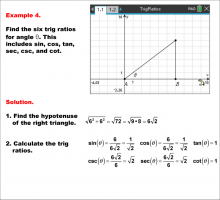
Math Example--Ratios and Rates--Trig Ratios--Example 4 Math Example--Ratios and Rates--Trig Ratios--Example 4 Math Example--Ratios and Rates--Trig Ratios--Example 4

This is part of a collection of math examples that focus on ratios and rates.

 Trig Expressions and Identities
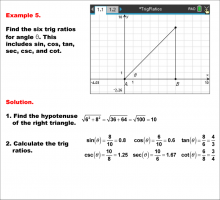
Math Example--Ratios and Rates--Trig Ratios--Example 5 Math Example--Ratios and Rates--Trig Ratios--Example 5 Math Example--Ratios and Rates--Trig Ratios--Example 5

This is part of a collection of math examples that focus on ratios and rates.

 Trig Expressions and Identities
Math Example--Ratios and Rates--Trig Ratios--Example 6 Math Example--Ratios and Rates--Trig Ratios--Example 6 Math Example--Ratios and Rates--Trig Ratios--Example 6

This is part of a collection of math examples that focus on ratios and rates.

 Trig Expressions and Identities
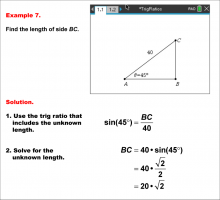
Math Example--Ratios and Rates--Trig Ratios--Example 7 Math Example--Ratios and Rates--Trig Ratios--Example 7 Math Example--Ratios and Rates--Trig Ratios--Example 7

This is part of a collection of math examples that focus on ratios and rates.

 Trig Expressions and Identities
Math Example--Ratios and Rates--Trig Ratios--Example 8 Math Example--Ratios and Rates--Trig Ratios--Example 8 Math Example--Ratios and Rates--Trig Ratios--Example 8

This is part of a collection of math examples that focus on ratios and rates.

 Trig Expressions and Identities
Math Example--Ratios and Rates--Trig Ratios--Example 9 Math Example--Ratios and Rates--Trig Ratios--Example 9 Math Example--Ratios and Rates--Trig Ratios--Example 9

This is part of a collection of math examples that focus on ratios and rates.

 Trig Expressions and Identities
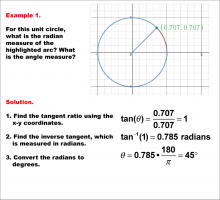
Math Example--Angle Concepts--Using Trig Ratios to Measure Radians--Example 1 Math Example--Angle Concepts--Using Trig Ratios to Measure Radians--Example 1 Math Example--Angle Concepts--Using Trig Ratios to Measure Radians--Example 1

Topic

Angles

Description

The image shows a unit circle with a highlighted arc and a point labeled (0.707, 0.707) on the circumference. The solution steps are shown on the right, explaining how to find the angle.

Example 1: The tangent ratio is calculated as tan(Θ) = 0.707 / 0.707 = 1. The inverse tangent is found as tan-1(1) = 0.785 radians. This is converted to degrees: Θ = 0.785 * (180 /π) = 45°.

 Trigonometric Functions
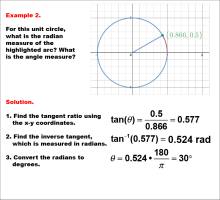
Math Example--Angle Concepts--Using Trig Ratios to Measure Radians--Example 2 Math Example--Angle Concepts--Using Trig Ratios to Measure Radians--Example 2 Math Example--Angle Concepts--Using Trig Ratios to Measure Radians--Example 2

Topic

Angles

Description

The image shows a unit circle with a highlighted arc and a point labeled (0.866, 0.5) on the circumference. The solution steps are displayed on the right, showing how to find the angle measure.

Example 2: The tangent ratio is calculated as tan(Θ) = 0.5 / 0.866 = 0.577. The inverse tangent is found as tan-1(0.577) = 0.524 radians. This is converted to degrees: Θ = 0.524 * (180 /π) = 30°.

 Trigonometric Functions
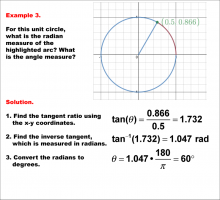
Math Example--Angle Concepts--Using Trig Ratios to Measure Radians--Example 3 Math Example--Angle Concepts--Using Trig Ratios to Measure Radians--Example 3 Math Example--Angle Concepts--Using Trig Ratios to Measure Radians--Example 3

Topic

Angles

Description

The image shows a unit circle with a highlighted arc and a point labeled (0.5, 0.866) on the circumference, connected by a tangent line from the origin to this point. The solution process for finding the angle measure is shown on the right side.

Example 3: The tangent ratio is calculated as tan(Θ) = 0.866 / 0.5 = 1.732. The inverse tangent is found as tan-1(1.732) = 1.047 radians. This is converted to degrees: Θ = 1.047 * (180 /π) = 60°.

 Trigonometric Functions