Illustrative Math Alignment: Grade 6 Unit 9

Topic

Rational Functions

Description

This math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (-x + 1). The image presents both the table of x-y coordinates and the resulting graph. The graph is plotted with points labeled at specific coordinates, demonstrating how the negative signs in both the numerator and denominator affect the graph's shape and position.

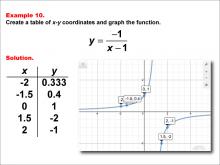
Topic

Rational Functions

Description

This math example focuses on creating a table of x-y coordinates and graphing the function y = -1 / (x - 1). The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The graph includes labeled points at certain coordinates, illustrating how the negative sign in the numerator and the constant in the denominator affect the graph's shape and position.

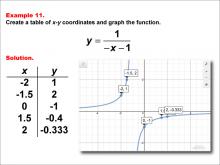
Topic

Rational Functions

Description

This math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x - 1). The image showcases both the table of x-y coordinates and the resulting graph. The graph is plotted with labeled points at given coordinates, illustrating how the negative sign and constant in the denominator affect the graph's shape and position.

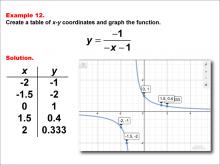
Topic

Rational Functions

Description

This math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (-x - 1). The image presents both the table of x-y coordinates and the resulting graph. The graph includes points labeled at specified coordinates, demonstrating how the negative signs in both the numerator and denominator, along with the constant, affect the graph's shape and position.

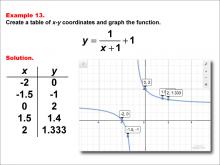
Topic

Rational Functions

Description

This math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / (x + 1) + 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The table contains specific x-y coordinates: (-2, 0), (-1.5, -1), (0, 2), (1.5, 1.4), (2, 1.333), which are plotted on the graph. This example illustrates how adding a constant to a rational function affects its graph.

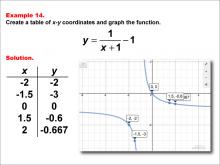
Topic

Rational Functions

Description

This math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (x + 1) - 1. The image showcases both the table of x-y coordinates and the resulting graph. The table contains specific x-y coordinates: (-2, -2), (-1.5, -3), (0, 0), (1.5, -0.6), (2, -0.667), which are plotted on the graph. This example illustrates how subtracting a constant from a rational function affects its graph.

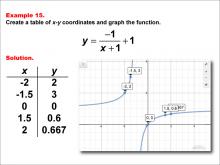
Topic

Rational Functions

Description

This math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (x + 1) + 1. The image presents both the table of x-y coordinates and the resulting graph. The table contains specific x-y coordinates: (-2, 2), (-1.5, 3), (0, 0), (1.5, 0.6), (2, 0.667), which are plotted on the graph. This example demonstrates how negating the numerator of a rational function and adding a constant affects its graph.

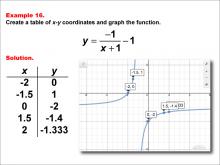
Topic

Rational Functions

Description

This math example focuses on creating a table of x-y coordinates and graphing the function y = -1 / (x + 1) - 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The table contains specific x-y coordinates: (-2, 0), (-1.5, 1), (0, -2), (1.5, -1.4), (2, -1.333), which are plotted on the graph. This example illustrates how negating the numerator of a rational function and subtracting a constant affects its graph.

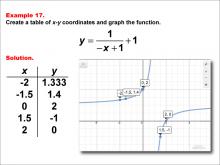
Topic

Rational Functions

Description

This math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x + 1) + 1. The image showcases both the table of x-y coordinates and the resulting graph. Points plotted include (-2, 1.333), (-1.5, 1.4), (0, 2), (1.5, -1), and (2, 0). The graph features a hyperbola with asymptotes, illustrating how negating the x-term in the denominator and adding a constant affects the graph's shape and position.

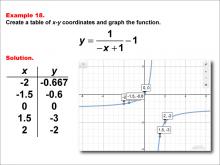
Topic

Rational Functions

Description

This math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x + 1) - 1. The image presents both the table of x-y coordinates and the resulting graph. Points plotted include (-2, -0.667), (-1.5, -0.6), (0, 0), (1.5, -3), and (2, -2). The graph shows a hyperbola with vertical and horizontal shifts, demonstrating how negating the x-term in the denominator and subtracting a constant affects the graph's shape and position.

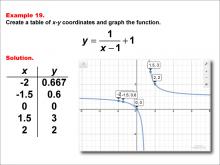
Topic

Rational Functions

Description

This math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / (x - 1) + 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. Points include (-2, 0.667), (-1.5, 0.6), (0, 0), (1.5, 3), and (2, 2). The graph is a hyperbola with asymptotes at x = 1 and y = 1, illustrating how subtracting a constant in the denominator and adding a constant to the entire fraction affects the graph's shape and position.

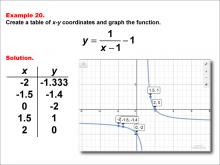
Topic

Rational Functions

Description

This math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (x - 1) - 1. The image showcases both the table of x-y coordinates and the resulting graph. The table contains specific x-y coordinates: (-2, -1.333), (-1.5, -1.4), (0, -2), (1.5, 1), and (2, 0). The graph is a hyperbola with shifted asymptotes at x = 1 and y = -1, illustrating how subtracting a constant in the denominator and from the entire fraction affects the graph's shape and position.

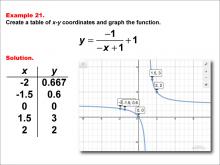
Topic

Rational Functions

Description

This math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = (-1) / (-x + 1) + 1. The image presents both the table of x-y coordinates and the resulting graph. It includes a table of x-y coordinates: (-2, 0.667), (-1.5, 0.6), (0, 0), (1.5, 3), and (2, 2). The graph is plotted on a grid, demonstrating how negating both the numerator and x-term in the denominator, while adding a constant to the entire fraction, affects the graph's shape and position.

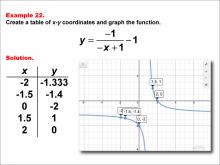
Topic

Rational Functions

Description

This math example focuses on creating a table of x-y coordinates and graphing the function y = (-1) / (-x + 1) - 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. It includes a table of x-y coordinates: (-2, -1.333), (-1.5, -1.4), (0, -2), (1.5, 1), and (2, 0). The graph is plotted on a grid, illustrating how negating both the numerator and x-term in the denominator, while subtracting a constant from the entire fraction, affects the graph's shape and position.

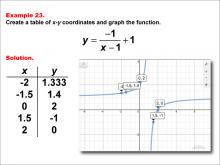
Topic

Rational Functions

Description

This math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = (-1) / (x - 1) + 1. The image shows both a table of x-y coordinates and the corresponding graph. The table includes points such as (-2, 1.333), (-1.5, 1.4), (0, 2), (1.5, -1), and (2, 0). The graph is plotted on a grid, illustrating how subtracting a constant in the denominator and adding a constant to the entire fraction affects the graph's shape and position.

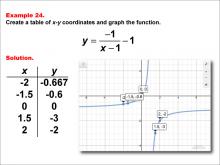
Topic

Rational Functions

Description

This math example focuses on creating a table of x-y coordinates and graphing the function y = (-1) / (x - 1) - 1. The image shows both a table of x-y coordinates and the corresponding graph. The table includes points such as (-2, -0.667), (-1.5, -0.6), (0, 0), (1.5, -3), and (2, -2). The graph is plotted on a grid, illustrating how subtracting constants both in the denominator and from the entire fraction affects the graph's shape and position.

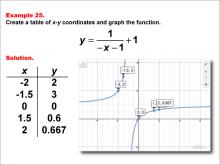
Topic

Rational Functions

Description

This math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = 1 / (-x - 1) + 1. The image showcases both the table of x-y coordinates and the resulting graph. The graph shows points plotted at (-2, 2), (-1.5, 3), (0, 0), (1.5, 0.6), and (2, 0.667), illustrating how negating both terms inside the parentheses and adding a constant to the entire fraction affects the graph's shape and position.

Topic

Rational Functions

Description

This math example focuses on creating a table of x-y coordinates and graphing the function y = 1 / (-x - 1) - 1. The image provided shows both a table of x-y coordinates and the corresponding graph of the function. The graph shows points plotted at (-2, 0), (-1.5, 1), (0, -2), (1.5, -1.4), and (2, -1.333), illustrating how negating both terms inside the parentheses and subtracting a constant from the entire fraction affects the graph's shape and position.

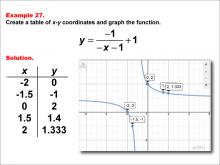
Topic

Rational Functions

Description

This math example illustrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (-x - 1) + 1. The image presents both the table of x-y coordinates and the resulting graph. The graph shows points plotted at (-2, 0), (-1.5, -1), (0, 2), (1.5, 1.4), and (2, 1.333), demonstrating how negating both the numerator and the terms inside the parentheses, while adding a constant to the entire fraction, affects the graph's shape and position.

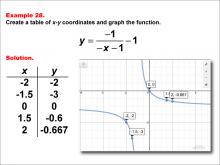
Topic

Rational Functions

Description

This math example demonstrates the creation of a table of x-y coordinates and the graphing of the function y = -1 / (-x - 1) - 1. The image showcases both the table of x-y coordinates and the resulting graph. The graph shows points plotted at (-2, -2), (-1.5, -3), (0, 0), (1.5, -0.6), and (2, -0.667), illustrating how negating both the numerator and the terms inside the parentheses, while subtracting a constant from the entire fraction, affects the graph's shape and position.

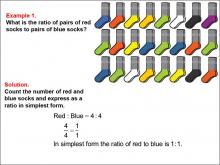
Topic

Ratios and Rates

Description

This math example focuses on understanding ratios using colored socks. The image displays a collection of red and blue socks, and students are asked to determine the ratio of red socks to blue socks. The solution demonstrates that there are 4 pairs of red socks and 4 pairs of blue socks, resulting in a ratio of 4 : 4, which simplifies to 1 : 1.

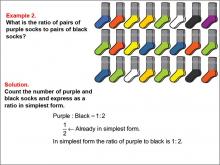
Topic

Ratios and Rates

Description

This example explores ratios using purple and black socks. The image shows a collection of socks, and students are asked to determine the ratio of purple socks to black socks. The solution reveals that there is 1 pair of purple socks and 2 pairs of black socks, resulting in a ratio of 1 : 2, which is already in its simplest form.

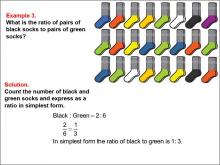
Topic

Ratios and Rates

Description

This example focuses on ratios using black and green socks. The image displays a collection of socks, and students are tasked with determining the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 6 pairs of green socks, resulting in a ratio of 2 : 6, which simplifies to 1 : 3.

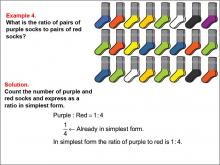
Topic

Ratios and Rates

Description

This example explores ratios using purple and red socks. The image shows a collection of socks, and students are asked to determine the ratio of purple socks to red socks. The solution reveals that there is 1 pair of purple socks and 4 pairs of red socks, resulting in a ratio of 1 : 4, which is already in its simplest form.

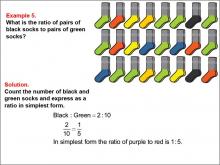
Topic

Ratios and Rates

Description

This example focuses on ratios using black and green socks among a variety of colored socks. The image displays pairs of socks in black, green, orange, yellow, blue, and red. Students are asked to determine the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 10 pairs of green socks, resulting in a ratio of 2 : 10, which simplifies to 1 : 5.

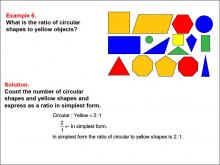
Topic

Ratios and Rates

Description

This example explores ratios using geometric shapes of different colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of circular shapes to yellow objects. The solution reveals that there are 2 circular shapes and 1 yellow object, resulting in a ratio of 2 : 1, which is already in its simplest form.

Topic

Ratios and Rates

Description

This example focuses on ratios using geometric shapes. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of triangles to quadrilaterals. The solution shows that there are 4 triangles and 6 quadrilaterals, resulting in a ratio of 4 : 6, which simplifies to 2 : 3.

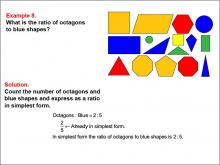
Topic

Ratios and Rates

Description

This example explores ratios using geometric shapes and colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of octagons to blue shapes. The solution reveals that there are 2 octagons and 5 blue shapes, resulting in a ratio of 2 : 5, which is already in its simplest form.

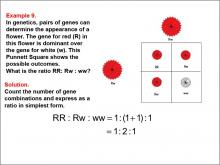
Topic

Ratios and Rates

Description

This example introduces the concept of ratios in genetics using a Punnett square. The image shows genetic combinations for a flower's color, including RR, Rw, and ww, with corresponding images of red and white flowers. Students are asked to determine the ratio of different gene combinations.

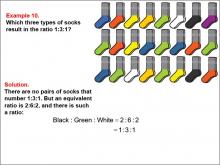
Topic

Ratios and Rates

Description

This example focuses on finding equivalent ratios using a collection of socks in various colors. The image shows socks arranged in rows, with black, green, white, and other colors present. Students are asked to find a ratio among three colors that is equivalent to 1 : 3 : 1.

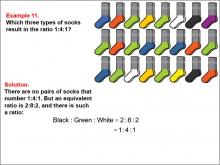
Topic

Ratios and Rates

Description

This example focuses on finding equivalent ratios using a collection of socks in various colors. The image shows socks arranged in rows, with black, green, white, and other colors present. Students are asked to find a ratio among three colors that is equivalent to 1 : 4 : 1.

Topic

Ratios and Rates

Description

This example explores the concept of similar triangles using ratios. The image shows a right triangle with sides labeled as 9, 12, and 15 units. Students are asked to determine if this triangle is similar to a standard 3-4-5 Pythagorean triplet triangle.

Understanding similar triangles is an important application of ratios in geometry. This example demonstrates how ratios can be used to compare the sides of triangles and determine similarity. By scaling the sides of a known triangle (3-4-5) and comparing them to the given triangle, students can see how ratios maintain proportionality in similar shapes.

Topic

Ratios and Rates

Description

This example focuses on verifying the similarity of triangles using ratios. The image shows a right triangle with sides labeled 25, 60, and 65 units. Students are guided through a step-by-step process to determine if this triangle is similar to a 5-12-13 right triangle.

Topic

Ratios and Rates

Description

This example explores the concept of special right triangles using ratios. The image shows a right triangle with sides labeled 3, 3 2 2 ​ , and 6 units. Students are guided through a step-by-step process to verify if this triangle is similar to a 30°-60°-90° triangle.

Topic

Ratios and Rates

Topic

Ratios and Rates

Description

This example focuses on converting units of speed and calculating rates. The image shows a car and calculations for converting speed from miles per hour to feet per second, given the distance traveled in miles and time in minutes.

Understanding unit conversions and rate calculations is crucial in many real-world applications, particularly in physics and engineering. This example demonstrates how to use ratios to convert between different units of speed, showcasing the practical application of mathematical concepts in everyday scenarios.

Topic

Ratios and Rates

Description

This example explores the concept of unit rates using the cost of gasoline. The image shows a red gasoline container, and students are asked to calculate the cost per gallon of gas given the total cost and volume.

Understanding unit rates is a fundamental skill in mathematics with numerous real-world applications. This example demonstrates how to calculate a unit rate by dividing the total cost by the total quantity, illustrating the practical use of division in everyday scenarios like purchasing gasoline.

Topic

Ratios and Rates

Description

This example focuses on calculating unit rates in a restaurant context. The image shows a hamburger, and students are asked to determine the cost per pound of ground beef given the total cost and weight purchased.

Understanding unit rates is essential in various real-world scenarios, particularly in business and economics. This example illustrates how to calculate a unit rate by dividing the total cost by the total quantity, demonstrating the practical application of division in a restaurant supply context.

Topic

Ratios and Rates

Description

This example explores the concept of flow rates using a backyard pool scenario. The image shows a backyard pool, and students are asked to calculate the rate of water flow in gallons per minute given the pool's capacity and the time taken to fill it.

Understanding flow rates is important in various fields, including engineering and physics. This example demonstrates how to calculate a rate by dividing the total volume by the total time, illustrating the practical application of division in real-world scenarios involving fluid dynamics.

Topic

Ratios and Rates

Description

This example focuses on unit conversion using the height of the Statue of Liberty. The image shows the Statue of Liberty, and students are asked to convert its height from feet to inches.

Understanding unit conversions is crucial in many fields, including science, engineering, and everyday life. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in real-world measurement scenarios.

Topic

Ratios and Rates

Description

This example focuses on unit conversion, specifically converting the height of the Statue of Liberty from feet to yards. The image shows the iconic Statue of Liberty, providing a real-world context for the mathematical problem.

Understanding unit conversions is crucial in many fields, including engineering, science, and everyday life. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of division and multiplication in real-world measurement scenarios.

Topic

Ratios and Rates

Description

This example explores unit conversion, specifically converting the height of the Statue of Liberty from feet to miles. The image depicts the Statue of Liberty, providing a tangible reference for the mathematical problem.

Understanding unit conversions, especially between widely different scales like feet and miles, is important in various fields such as geography, engineering, and urban planning. This example showcases how to use a conversion factor to change units, demonstrating the practical application of division and multiplication in real-world measurement scenarios.

Topic

Ratios and Rates

Description

This example focuses on unit conversion, specifically converting the height of columns from inches to feet. The image shows columns, providing a visual context for the mathematical problem.

Understanding unit conversions between inches and feet is crucial in many practical applications, including construction, interior design, and everyday measurements. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of division and multiplication in real-world measurement scenarios.

Topic

Ratios and Rates

Description

This example explores unit conversion in a sports context, specifically converting a quarterback's pass distance from yards to feet. The image shows a silhouette of a quarterback throwing a football, providing a real-world scenario for the mathematical problem.

Understanding unit conversions between yards and feet is crucial in many sports, especially American football. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in sports-related measurement scenarios.

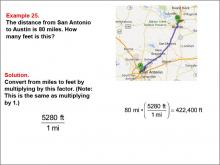
Topic

Ratios and Rates

Description

This example focuses on unit conversion in a geographic context, specifically converting the distance between San Antonio and Austin from miles to feet. The image shows a map of the route between these two Texas cities, providing a real-world scenario for the mathematical problem.

Understanding unit conversions between miles and feet is important in various fields, including geography, transportation, and urban planning. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in distance-related measurement scenarios.

Topic

Ratios and Rates

Description

This example focuses on time unit conversion, specifically converting hours to minutes in the context of a standardized test duration. The image shows a clock, providing a visual representation of time for the mathematical problem.

Understanding time unit conversions is crucial in many aspects of daily life, including scheduling, time management, and test-taking. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in time-related scenarios.

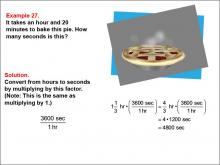
Topic

Ratios and Rates

Description

This example explores time unit conversion, specifically converting hours and minutes to seconds in the context of baking a pie. The image shows a steaming pie, providing a real-world scenario for the mathematical problem.

Understanding time unit conversions, especially when dealing with mixed units, is important in various fields such as cooking, manufacturing, and project management. This example demonstrates how to use conversion factors to change units, illustrating the practical application of multiplication in time-related scenarios.

Topic

Ratios and Rates

Description

This example focuses on time unit conversion in a sports context, specifically converting minutes and seconds to seconds for a horse race lap time. The image shows a horse, providing a visual context for the mathematical problem.

Understanding time unit conversions is crucial in many sports, especially those involving racing and timed events. This example demonstrates how to use conversion factors to change units and add different time units, illustrating the practical application of multiplication and addition in sports-related time scenarios.

Topic

Ratios and Rates

Description

This example explores time unit conversion in an IT context, specifically converting seconds to minutes for user session duration. The image shows a computer tower, providing a real-world scenario for the mathematical problem.

Understanding time unit conversions is crucial in many technological fields, especially in IT and user experience analysis. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of division in time-related measurement scenarios. It also introduces the concept of mixed numbers in the result.

Topic

Ratios and Rates

Description

This example focuses on time unit conversion in an IT context, specifically converting seconds to hours for user session duration. The image shows a computer tower, providing a real-world scenario for the mathematical problem.