
Illustrative Math Alignment: Grade 6 Unit 9
Putting it All Together
Lesson 4: How Do We Choose?
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topics |
|---|---|---|---|

|
Math Example: Fraction Operations--Dividing Fractions: Example 15 | Dividing Fractions: Example 15TopicFraction Operations DescriptionThis example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. The result is a mixed number. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations. |
Fractions and Mixed Numbers |
|
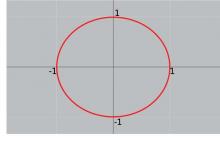
Math Clip Art--Geometry Concepts--Circle Illustrations--Unit Circle | Math Clip Art--Geometry Concepts--Circle Illustrations--Unit Circle
This is part of a collection of math clip art images about selected topics in Geometry. Also look at our Geometry Basics math clip art collection. |
Definition of a Circle and Applications of Coordinate Geometry |
|
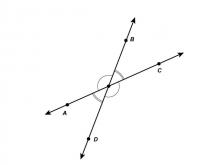
Math Clip Art--Angle Illustrations--Vertical Angles--Labeled | Math Clip Art--Angle Illustrations--Vertical Angles--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
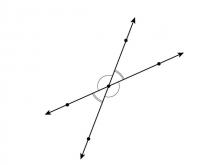
Math Clip Art--Angle Illustrations--Vertical Angles--Unlabeled | Math Clip Art--Angle Illustrations--Vertical Angles--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
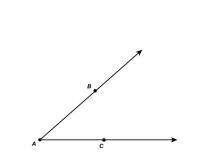
Math Clip Art--Angle Illustrations--Acute Angle--Labeled | Math Clip Art--Angle Illustrations--Acute Angle--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Acute Angle--Unlabeled | Math Clip Art--Angle Illustrations--Acute Angle--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Adjacent Angles--Labeled | Math Clip Art--Angle Illustrations--Adjacent Angles--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Adjacent Angles--Unlabeled | Math Clip Art--Angle Illustrations--Adjacent Angles--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Angle Bisector--Labeled | Math Clip Art--Angle Illustrations--Angle Bisector--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Angle Bisector--Unlabeled | Math Clip Art--Angle Illustrations--Angle Bisector--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Angle--Labeled | Math Clip Art--Angle Illustrations--Angle--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Angle--Unlabeled | Math Clip Art--Angle Illustrations--Angle--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle | Math Clip Art--Circle Illustrations--CircleTopicGeometry Concepts DescriptionThis clip art illustrates a basic circle, which is a fundamental shape in geometry. A circle is defined as the set of all points in a plane that are equidistant from a central point. This image serves as a visual representation of this concept, showcasing the perfect symmetry and continuous curvature that characterize circles. |
Definition of a Circle |
|
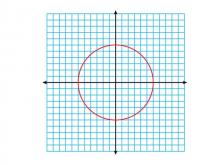
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle Centered at Origin of Coordinate Grid | Math Clip Art--Circle Illustrations--Circle Centered at Origin of Coordinate GridTopicGeometry Concepts DescriptionThis clip art depicts a circle centered at the origin (0,0) of a coordinate grid. It illustrates the relationship between circles and the Cartesian coordinate system, a fundamental concept in analytic geometry. The image shows how a circle's position can be defined in relation to the x and y axes. |
Definition of a Circle |
|
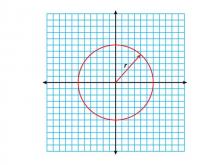
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle Centered at Origin of Coordinate Grid--with Radius Labeled | Math Clip Art--Circle Illustrations--Circle Centered at Origin of Coordinate Grid--with Radius LabeledTopicGeometry Concepts DescriptionThis clip art shows a circle centered at the origin of a coordinate grid with its radius clearly labeled. This illustration is crucial for understanding the relationship between a circle's radius and its equation in the coordinate plane. The labeled radius helps visualize how the distance from the center to any point on the circle remains constant, which is the defining property of a circle. |
Definition of a Circle |
|
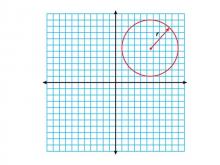
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle Centered in Q1 | Math Clip Art--Circle Illustrations--Circle Centered in Q1TopicGeometry Concepts DescriptionThis clip art illustrates a circle centered in the first quadrant (Q1) of the coordinate plane. This representation is crucial for understanding how the position of a circle's center affects its equation and properties. In Q1, both x and y coordinates of the center are positive, which influences the circle's equation and its intersection with the axes. |
Definition of a Circle |
|
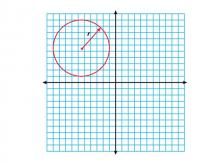
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle Centered in Q2 | Math Clip Art--Circle Illustrations--Circle Centered in Q2TopicGeometry Concepts DescriptionThis clip art shows a circle centered in the second quadrant (Q2) of the coordinate plane. In Q2, the x-coordinate of the center is negative while the y-coordinate is positive. This positioning is crucial for understanding how the location of a circle's center affects its equation and its relationship with the coordinate axes. |
Definition of a Circle |
|
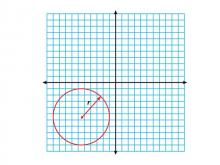
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle Centered in Q3 | Math Clip Art--Circle Illustrations--Circle Centered in Q3TopicGeometry Concepts DescriptionThis clip art depicts a circle centered in the third quadrant (Q3) of the coordinate plane. In Q3, both the x and y coordinates of the center are negative. This positioning is essential for understanding how the location of a circle's center influences its equation and its interactions with the coordinate axes. |
Definition of a Circle |
|
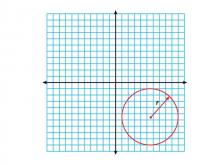
Math Clip Art--Geometry Concepts--Circle Illustrations--Circle Centered in Q4 | TopicGeometry Concepts DescriptionThis clip art illustrates a circle centered in the fourth quadrant (Q4) of the coordinate plane. In Q4, the x-coordinate of the center is positive while the y-coordinate is negative. This positioning is crucial for understanding how the location of a circle's center affects its equation and its relationship with the coordinate axes. |
Definition of a Circle |
|
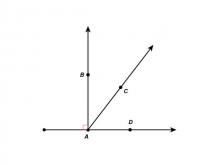
Math Clip Art--Angle Illustrations--Complementary Angles--Labeled | Math Clip Art--Angle Illustrations--Complementary Angles--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Complementary Angles--Unlabeled | Math Clip Art--Angle Illustrations--Complementary Angles--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Exterior Angle of a Triangle--Labeled | Math Clip Art--Angle Illustrations--Exterior Angle of a Triangle--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Exterior Angle of a Triangle--Unlabeled | Math Clip Art--Angle Illustrations--Exterior Angle of a Triangle--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Obtuse Angle--Labeled | Math Clip Art--Angle Illustrations--Obtuse Angle--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Obtuse Angle--Unlabeled | Math Clip Art--Angle Illustrations--Obtuse Angle--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |

|
Math Clip Art--Function Concepts--Graphs of Functions and Relations--Rational Function Graph | Math Clip Art--Function Concepts--Graphs of Functions and Relations--Rational Function GraphTopicFunctions DescriptionThis clip art depicts a rational function graph. Rational functions are quotients of polynomials and can have a wide variety of shapes depending on the degrees of the numerator and denominator. They generally pass the vertical line test and are thus functions, though they may have discontinuities. |
Rational Functions and Equations |
|
Math Clip Art--Angle Illustrations--Right Angle--Labeled | Math Clip Art--Angle Illustrations--Right Angle--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Right Angle--Unlabeled | Math Clip Art--Angle Illustrations--Right Angle--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Straight Angle--Labeled | Math Clip Art--Angle Illustrations--Straight Angle--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
Math Clip Art--Angle Illustrations--Straight Angle--Unlabeled | Math Clip Art--Angle Illustrations--Straight Angle--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
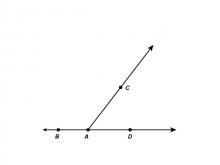
Math Clip Art--Angle Illustrations--Supplementary Angles--Labeled | Math Clip Art--Angle Illustrations--Supplementary Angles--Labeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |
|
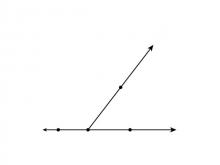
Math Clip Art--Angle Illustrations--Supplementary Angles--Unlabeled | Math Clip Art--Angle Illustrations--Supplementary Angles--Unlabeled
This is part of a collection of clip art images showing different types of angles. Each type of angle measure includes a labeled and unlabeled version. |
Angles and Applications of Angles and Planes |

|
Definition--Rationals and Radicals--Cube Root | Cube RootTopicRationals and Radicals DefinitionThe cube root of a number is a value that, when multiplied by itself three times, gives the original number. DescriptionThe cube root is a fundamental concept in Radical Numbers, Expressions, Equations, and Functions. It is the inverse operation of raising a number to the power of three. Understanding cube roots is crucial for solving equations involving cubic terms and for simplifying radical expressions. Cube roots also appear in various real-world applications, such as calculating volumes and in certain physics equations. They are an integral part of higher-level mathematics, including algebra and calculus. |
Radical Expressions |

|
Definition--Rationals and Radicals--Extraneous Solution | Extraneous SolutionTopicRationals and Radicals DefinitionAn extraneous solution is a solution derived from an equation that is not a valid solution to the original equation. DescriptionExtraneous solutions often arise in the context of Rational and Radical Equations. They are solutions that appear during the process of solving an equation but do not satisfy the original equation. This can happen when both sides of an equation are squared or when other operations introduce additional solutions. |
Rational Functions and Equations |
|
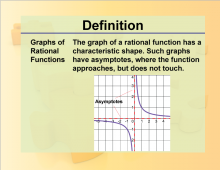
Definition--Rationals and Radicals--Graphs of Rational Functions | Graphs of Rational FunctionsTopicRationals and Radicals DefinitionGraphs of rational functions are visual representations of equations involving rational expressions. DescriptionGraphs of rational functions are fundamental in the study of Rational Numbers, Expressions, Equations, and Functions. They help in understanding the behavior of these functions, including their asymptotes, intercepts, and regions of increase and decrease. |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Inverse Variation | Inverse VariationTopicRationals and Radicals DefinitionInverse variation describes a relationship between two variables in which the product is a constant. When one variable increases, the other decreases proportionally. |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Irrational Number 2 | Irrational Number 2TopicRationals and Radicals DefinitionAn irrational number is a number that cannot be expressed as a ratio of two integers. Its decimal form is non-repeating and non-terminating. |
Rational Expressions |

|
Definition--Rationals and Radicals--nth Root | nth RootTopicRationals and Radicals DefinitionThe nth root of a number is a value that, when raised to the power of n, gives the original number. It is denoted as n√a DescriptionThe nth Root is a fundamental concept in the study of Radical Numbers, Expressions, Equations, and Functions. It generalizes the idea of square roots and cube roots to any positive integer n. For example, the cube root of 8 is 2 because 23=8 |
Radical Expressions |

|
Definition--Order of Operations | Definition--Order of Operations
Watch the following video on Order of Operations. (The transcript is included.) Video Transcript
A numerical expression includes numbers and operation symbols, addition, subtraction, multiplication, and division. Because addition is commutative, adding from left to right, or right to left, gives you the same result. The expressions 2 + 3 and 3 + 2 give the same result. But this isn't the case with all operations. Subtraction isn't commutative. |
Numerical Expressions and Variable Expressions |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Rationals and Radicals--Radical Expression | Radical ExpressionTopicRationals and Radicals DefinitionA radical expression is an expression that contains a radical symbol, which indicates the root of a number. DescriptionRadical Expressions are a core component of Radical Numbers, Expressions, Equations, and Functions. These expressions involve roots, such as square roots, cube roots, or higher-order roots, and are denoted by the radical symbol (√). For example, the expression √16 |
Radical Expressions |

|
Definition--Rationals and Radicals--Radical Function | Radical FunctionTopicRationals and Radicals DefinitionA radical function is a function that contains a radical expression with the independent variable in the radicand. DescriptionRadical Functions are a vital part of Radical Numbers, Expressions, Equations, and Functions. These functions involve radicals, such as square roots or cube roots, with the independent variable inside the radical. For example, the function f(x)=√x |
Radical Expressions |

|
Definition--Rationals and Radicals--Radical Symbol | Radical SymbolTopicRationals and Radicals DefinitionThe radical symbol (√) is used to denote the root of a number, such as a square root or cube root. DescriptionThe Radical Symbol is a fundamental notation in the study of Radical Numbers, Expressions, Equations, and Functions. This symbol (√) indicates the root of a number, with the most common being the square root. For example, the expression √25 |
Radical Expressions |

|
Definition--Rationals and Radicals--Radicand | RadicandTopicRationals and Radicals DefinitionThe radicand is the number or expression inside the radical symbol that is being rooted. DescriptionThe Radicand is a key component in the study of Radical Numbers, Expressions, Equations, and Functions. It is the number or expression inside the radical symbol that is being rooted. For example, in the expression √49 |
Radical Expressions |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Rationals and Radicals--Rational Expressions | Rational ExpressionsTopicRationals and Radicals DefinitionRational expressions are fractions in which the numerator and/or the denominator are polynomials. DescriptionRational Expressions are a fundamental aspect of Rational Numbers, Expressions, Equations, and Functions. These expressions are fractions where the numerator and/or the denominator are polynomials. Simplifying rational expressions often involves factoring the polynomials and canceling common factors. For example, the rational expression x2−1x−1 can be simplified to x + 1, provided that x≠1 |
Rational Expressions |

|
Definition--Rationals and Radicals--Rational Functions | Rational FunctionsTopicRationals and Radicals DefinitionRational functions are functions that are the ratio of two polynomials. DescriptionRational Functions are a key concept in the study of Rational Numbers, Expressions, Equations, and Functions. These functions are the ratio of two polynomials, such as f(x)=P(x)Q(x) where P(x) and Q(x) are polynomials. Understanding rational functions involves analyzing their behavior, including identifying asymptotes, intercepts, and discontinuities. For example, the function f(x)=1x |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Rational Numbers | Rational NumbersTopicRationals and Radicals DefinitionRational numbers are numbers that can be expressed as a ratio of two integers, where the denominator is not zero. |
Rational Functions and Equations |