Illustrative Math Alignment: Grade 6 Unit 9

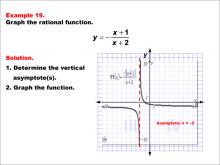
Topic

Rational Functions

Description

This example presents the graph of the rational function y = -(x + 1) / (x + 2). The graph features a single vertical asymptote at x = -2, indicated by a dashed red line. Students are tasked with graphing the function and determining its vertical asymptote.

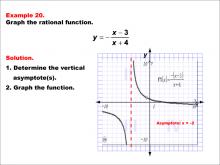
Topic

Rational Functions

Description

This example showcases the graph of the rational function y = -(x - 3) / (x + 4). The graph features a vertical asymptote at x = -4, but it is incorrectly labeled as x = -2. Students are asked to graph the function and identify its vertical asymptote.

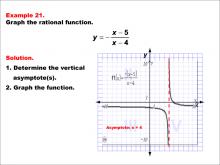
Topic

Rational Functions

Description

This example illustrates the graph of the rational function y = -(x - 5) / (x - 4). The graph features a vertical asymptote at x = 4, which is correctly labeled. Students are tasked with graphing the function and determining its vertical asymptote.

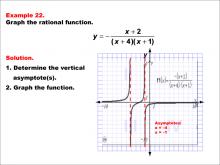
Topic

Rational Functions

Description

This example presents the graph of the rational function y = -(x + 2) / ((x + 4)(x + 1)). The graph features vertical asymptotes at x = -4 and x = -1. Students are asked to graph the function and identify its vertical asymptotes.

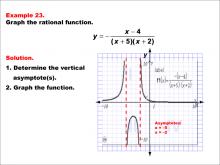
Topic

Rational Functions

Description

This example illustrates the graph of the rational function y = -(x - 4) / ((x + 5)(x + 2)). The graph features vertical asymptotes at x = -5 and x = -2. Students are tasked with graphing the function and determining its vertical asymptotes.

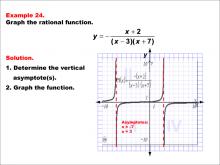
Topic

Rational Functions

Description

This example showcases the graph of the rational function y = -(x + 2) / ((x - 3)(x + 7)). The graph features vertical asymptotes at x = -7 and x = 3. Students are asked to graph the function and identify its vertical asymptotes.

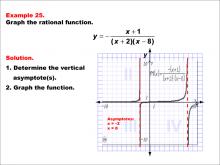
Topic

Rational Functions

Description

This example illustrates the graph of the rational function y = -(x + 1) / ((x + 2)(x - 8)). The graph features vertical asymptotes at x = -2 and x = 8. Students are tasked with graphing the function and determining its vertical asymptotes.

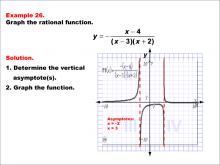
Topic

Rational Functions

Description

This example showcases the graph of the rational function y = -(x - 4) / ((x - 3)(x + 2)). The graph features vertical asymptotes at x = -2 and x = 3. Students are asked to graph the function and identify its vertical asymptotes.

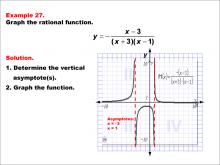
Topic

Rational Functions

Description

This example presents the graph of the rational function y = -(x - 3) / ((x + 3)(x - 1)). The graph features vertical asymptotes at x = -3 and x = 1. Students are tasked with graphing the function and determining its vertical asymptotes.

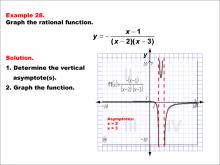
Topic

Rational Functions

Description

This example illustrates the graph of the rational function y = -(x - 1) / ((x - 2)(x - 3)). The graph features vertical asymptotes at x = 2 and x = 3, marked with dashed red lines on the coordinate plane. Students are asked to graph the function and identify its vertical asymptotes.

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Topic

Fraction Operations

Description

This example demonstrates the concept of adding fractions with like denominators. The image likely shows two fractions that need to be added together. Since there is a common denominator, the numerators are then added, and the resulting fraction does not need to be simplified. This process involves skills such as recognizing common denominators, adding numerators, and identifying a fraction in simplest form..

For a complete collection of math examples related to Adding Fractions click on this link: Math Examples: Adding Fractions Collection.

Topic

Fraction Operations

Description

This example illustrates the addition of fractions with common denominators. The key concept is to identify the common denominator. The numerators are summed, and the final fraction is simplified. Skills required include recognizing common denominators, adding numerators, and simplifying the result.

For a complete collection of math examples related to Adding Fractions click on this link: Math Examples: Adding Fractions Collection.

Topic

Fraction Operations

Description

This example focuses on adding fractions that have different denominators. The image depicts the fractions and the steps needed to add them. The process involves finding a common denominator, converting the fractions to have this common denominator, adding the numerators, and simplifying the resulting fraction. In this example, one denominator is a multiple of the other denominator. Skills involved include finding the least common multiple, converting fractions, adding numerators, and simplifying the final fraction.

Topic

Fraction Operations

Description

This example demonstrates the addition of fractions with unlike denominators. The image shows the fractions and the method to add them. One denominator is a multiple of the other. The key steps include identifying a common denominator, rewriting the fractions with this denominator, summing the numerators, and simplifying the resulting fraction. Skills required include determining the least common multiple, adjusting fractions, performing addition, and simplifying the fraction.

Topic

Fraction Operations

Description

This example highlights the process of adding fractions with different denominators. The image illustrates the fractions and the steps to add them. The process involves finding a common denominator, converting the fractions to have this common denominator, adding the numerators, and simplifying the result. Skills involved include calculating the least common multiple, adjusting numerators, performing addition, and simplifying the fraction (or recognizing when a fraction is already in simplest form).

Topic

Fraction Operations

Description

This example covers the addition of fractions with unlike denominators. The image shows the fractions and the method to add them. The process involves identifying a common denominator, rewriting the fractions with this denominator, summing the numerators, and simplifying the resulting fraction. Skills required include determining the least common multiple, adjusting fractions, performing addition, and simplifying the fraction.

Topic

Fraction Operations

Description

This example illustrates the addition of fractions with different denominators. The image provides a visual representation of two fractions being added. The key concept is to align the fractions by finding a common denominator, which is essential for adding fractions accurately. The fractions are rewritten with this common denominator, the numerators are summed, and the final fraction is simplified. Skills required include calculating the least common multiple, adjusting numerators, performing arithmetic operations, and simplifying the result (or recognizing when a fraction is already in simplest form).

Topic

Fraction Operations

Description

This example focuses on adding fractions that have different denominators. The image depicts the fractions and the steps needed to add them. The process involves finding a common denominator, converting the fractions to have this common denominator, adding the numerators, and simplifying the resulting fraction. Skills involved include finding the least common multiple, converting fractions, adding numerators, and simplifying the final fraction.

Topic

Fraction Operations

Description

This example demonstrates the concept of adding fractions with unlike denominators. The image shows two fractions that need to be added together. To solve this, one must first find a common denominator, which involves determining the least common multiple of the denominators. Once a common denominator is found, the fractions are converted to equivalent fractions with this common denominator. The numerators are then added, and the resulting fraction is simplified if necessary. This process involves skills such as finding common multiples, converting fractions, performing addition, and simplifying fractions.

Topic

Fraction Operations

Description

This example highlights the process of adding fractions with different denominators. The image illustrates the fractions and the steps to add them. The process involves finding a common denominator, converting the fractions to have this common denominator, adding the numerators, and simplifying the result. Skills involved include calculating the least common multiple, adjusting numerators, performing addition, and simplifying the fraction.

Topic

Fraction Operations

Description

This example covers the addition of fractions with unlike denominators. The image shows the fractions and the method to add them. The process involves identifying a common denominator, rewriting the fractions with this denominator, summing the numerators, and simplifying the resulting fraction (or recognizing when a fraction is already in simplest form). Skills required include determining the least common multiple, adjusting fractions, performing addition, and simplifying the fraction.

Topic

Fraction Operations

Description

This example focuses on dividing fractions, a fundamental concept in mathematics that involves inverting the divisor and multiplying it by the dividend. The image illustrates a step-by-step process of solving a division problem involving fractions, demonstrating the concept of reciprocal multiplication. The specific skills involved include understanding reciprocal relationships, performing multiplication of fractions, and simplifying the result. This example helps reinforce the understanding of how dividing by a fraction is equivalent to multiplying by its reciprocal, a key skill in fraction operations.

Topic

Fraction Operations

Description

This example illustrates the process of dividing fractions by converting the division into multiplication using the reciprocal of the divisor. The visual representation helps learners visualize the transformation and subsequent multiplication, emphasizing the importance of understanding reciprocal operations. Skills involved include recognizing equivalent fractions, performing multiplication, and simplifying fractions to their lowest terms. This example is crucial for students to grasp how division of fractions simplifies into a multiplication problem, enhancing their problem-solving capabilities in fraction arithmetic.

Topic

Fraction Operations

Description

This example demonstrates dividing fractions by illustrating the conversion of the division operation into multiplication by the reciprocal. The image serves as a guide to understanding the method of flipping the second fraction and multiplying, showcasing the concept of reciprocal multiplication. Key skills include identifying reciprocal relationships, multiplying fractions, and simplifying results. This example is instrumental in helping students understand the mechanics of dividing fractions, which is a pivotal skill in mastering fraction operations.

Topic

Fraction Operations

Description

This example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic.

Topic

Fraction Operations

Description

This example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations.

Topic

Fraction Operations

Description

This example demonstrates the division of fractions by illustrating the conversion of division into multiplication using the reciprocal of the divisor. The visual guide helps learners understand the transformation and the subsequent multiplication process. Key skills include identifying reciprocal relationships, executing multiplication, and simplifying fractions. This example is instrumental in building a solid understanding of how dividing fractions simplifies into a multiplication problem, enhancing students' problem-solving skills in fraction arithmetic.

Topic

Fraction Operations

Description

This example focuses on dividing fractions by converting the division into multiplication using the reciprocal of the divisor. The image visually represents the process, emphasizing the importance of understanding reciprocal operations. Skills involved include recognizing equivalent fractions, performing multiplication, and simplifying fractions to their lowest terms. This example is crucial for students to grasp how division of fractions simplifies into a multiplication problem, enhancing their problem-solving capabilities in fraction arithmetic.

Topic

Fraction Operations

Description

This example demonstrates the division of fractions by illustrating the conversion of the division operation into multiplication by the reciprocal. The image serves as a guide to understanding the method of flipping the second fraction and multiplying, showcasing the concept of reciprocal multiplication. Key skills include identifying reciprocal relationships, multiplying fractions, and simplifying results. This example is instrumental in helping students understand the mechanics of dividing fractions, which is a pivotal skill in mastering fraction operations.

Topic

Fraction Operations

Description

This example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. In this example the quotient equals 1. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic.

Topic

Fraction Operations

Description

This example illustrates the division of fractions by converting the operation into multiplication using the reciprocal of the divisor. The image provides a clear step-by-step guide, emphasizing the importance of reciprocal multiplication. In this example the result is a mixed number. Skills involved include recognizing and applying reciprocal relationships, performing multiplication, and simplifying fractions. This example is crucial for understanding the fundamental principle that dividing by a fraction is equivalent to multiplying by its reciprocal, a key concept in fraction operations.

Topic

Fraction Operations

Description

This example demonstrates the division of fractions by illustrating the conversion of division into multiplication using the reciprocal of the divisor. The visual guide helps learners understand the transformation and the subsequent multiplication process. In this example, the result is a mixed number. Key skills include identifying reciprocal relationships, executing multiplication, and simplifying fractions. This example is instrumental in building a solid understanding of how dividing fractions simplifies into a multiplication problem, enhancing students' problem-solving skills in fraction arithmetic.

Topic

Fraction Operations

Description

This example focuses on dividing fractions by converting the division into multiplication using the reciprocal of the divisor. The image visually represents the process, emphasizing the importance of understanding reciprocal operations. In this example the result is a mixed number. Skills involved include recognizing equivalent fractions, performing multiplication, and simplifying fractions to their lowest terms. This example is crucial for students to grasp how division of fractions simplifies into a multiplication problem, enhancing their problem-solving capabilities in fraction arithmetic.

Topic

Fraction Operations

Description

This example demonstrates the division of fractions by illustrating the conversion of the division operation into multiplication by the reciprocal. The image serves as a guide to understanding the method of flipping the second fraction and multiplying, showcasing the concept of reciprocal multiplication. The result is a mixed number. Key skills include identifying reciprocal relationships, multiplying fractions, and simplifying results. This example is instrumental in helping students understand the mechanics of dividing fractions, which is a pivotal skill in mastering fraction operations.

Topic

Fraction Operations

Description

This example focuses on the division of fractions by utilizing the reciprocal of the divisor. The process is visually depicted, allowing learners to follow the transformation from division to multiplication. The result is a mixed number. Essential skills include understanding the concept of reciprocals, executing multiplication of fractions, and simplifying the final result. This example aids in reinforcing the understanding of how dividing fractions is essentially multiplying by the inverse, a critical concept in fraction arithmetic.