
Illustrative Math Alignment: Grade 7 Unit 1
Scale Drawings
Lesson 4: Scaled Relationships
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Clip Art--Applications of Proportions--Exchange Rates 7 | Math Clip Art--Applications of Proportions--Exchange Rates 7 This is a collection of clip art images that show an application of proportional reasoning in the context of currency exchange rates. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Proportions--Exchange Rates 8 | Math Clip Art--Applications of Proportions--Exchange Rates 8 This is a collection of clip art images that show an application of proportional reasoning in the context of currency exchange rates. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Proportions--Exchange Rates 9 | Math Clip Art--Applications of Proportions--Exchange Rates 9 This is a collection of clip art images that show an application of proportional reasoning in the context of currency exchange rates. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 1 | Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 1 This is a collection of clip art images that show an application of proportional reasoning in the context of carbon dating. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 2 | Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 2 This is a collection of clip art images that show an application of proportional reasoning in the context of carbon dating. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 3 | Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 3 This is a collection of clip art images that show an application of proportional reasoning in the context of carbon dating. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 4 | Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 4 This is a collection of clip art images that show an application of proportional reasoning in the context of carbon dating. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 5 | Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 5 This is a collection of clip art images that show an application of proportional reasoning in the context of carbon dating. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 6 | Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 6 This is a collection of clip art images that show an application of proportional reasoning in the context of carbon dating. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 7 | Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 7 This is a collection of clip art images that show an application of proportional reasoning in the context of carbon dating. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 8 | Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 8 This is a collection of clip art images that show an application of proportional reasoning in the context of carbon dating. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 9 | Math Clip Art--Applications of Ratios and Proportions--Carbon Dating 9 This is a collection of clip art images that show an application of proportional reasoning in the context of carbon dating. |
Ratios and Rates and Proportions |
|
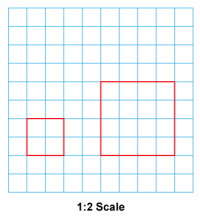
Math Clip Art--Geometry Concepts--Scale Drawing--01 | Math Clip Art--Scale Drawing--01TopicGeometry Concepts DescriptionThis image depicts a scale drawing of a square that has been scaled up by a factor of 1:2. This means that each side of the square in the drawing is twice the length of the corresponding side in the actual object. Scale drawings are essential for accurately representing objects in a manageable size while maintaining proportionality. Teacher's Script: "Observe this scale drawing of a square. How does the 1:2 scale factor help us understand the relationship between the drawing and the actual square? What are some real-world applications of scaling up objects, such as in architecture or design?" |
Proportions |

|
Math Clip Art--Geometry Concepts--Scale Drawing--02 | Math Clip Art--Scale Drawing--02TopicGeometry Concepts DescriptionThis image illustrates a scale drawing of a square that has been scaled up by a factor of 1:3. Each side of the square in the drawing is three times the length of the corresponding side in the actual object. This scaling helps in visualizing larger versions of objects while maintaining accurate proportions. Teacher's Script: "Look at this scale drawing of a square. How does the 1:3 scale factor affect the dimensions of the drawing compared to the actual square? What are some mathematical concepts you can explore using scale drawings, such as ratios or proportions?" |
Proportions |
|
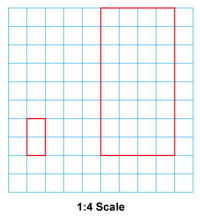
Math Clip Art--Geometry Concepts--Scale Drawing--03 | Math Clip Art--Scale Drawing--03TopicGeometry Concepts DescriptionThis image shows a scale drawing of a rectangle that has been scaled up by a factor of 1:4. Each side of the rectangle in the drawing is four times the length of the corresponding side in the actual object. This scaling is useful for enlarging objects while maintaining their proportional dimensions. Teacher's Script: "Examine this scale drawing of a rectangle. How does the 1:4 scale factor influence the size of the drawing compared to the actual rectangle? What are some real-world applications of scaling up objects, such as in engineering or construction?" |
Proportions |

|
Math Clip Art--Geometry Concepts--Scale Drawing--04 | Math Clip Art--Scale Drawing--04TopicGeometry Concepts DescriptionThis image illustrates a scale drawing of a rectangle that has been scaled up by a factor of 1:5. Each side of the rectangle in the drawing is five times the length of the corresponding side in the actual object. Scale drawings like this are crucial for visualizing larger versions of objects while maintaining accurate proportions. Teacher's Script: "Observe this scale drawing of a rectangle. How does the 1:5 scale factor affect the dimensions of the drawing compared to the actual rectangle? What are some mathematical concepts you can explore using scale drawings, such as ratios or proportions?" |
Proportions |
|
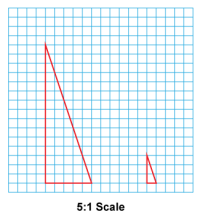
Math Clip Art--Geometry Concepts--Scale Drawing--05 | Math Clip Art--Scale Drawing--05TopicGeometry Concepts DescriptionThis image depicts a scale drawing of a right triangle that has been scaled down by a factor of 5:1. This means each side of the triangle in the drawing is one-fifth the length of the corresponding side in the actual object. Scaling down is useful for creating manageable representations of larger objects. Teacher's Script: "Examine this scale drawing of a right triangle. How does the 5:1 scale factor help us understand the relationship between the drawing and the actual triangle? What are some real-world applications of scaling down objects, such as in model making or map creation?" |
Proportions |
|
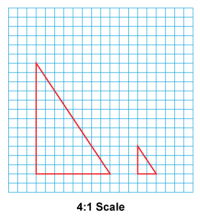
Math Clip Art--Geometry Concepts--Scale Drawing--06 | Math Clip Art--Scale Drawing--06TopicGeometry Concepts DescriptionThis image illustrates a scale drawing of a right triangle that has been scaled down by a factor of 4:1. Each side of the triangle in the drawing is one-fourth the length of the corresponding side in the actual object. This scaling helps in visualizing smaller versions of objects while maintaining accurate proportions. Teacher's Script: "Observe this scale drawing of a right triangle. How does the 4:1 scale factor affect the dimensions of the drawing compared to the actual triangle? What are some mathematical concepts you can explore using scale drawings, such as ratios or proportions?" |
Proportions |
|
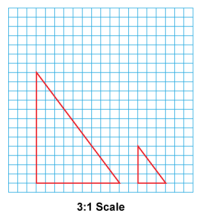
Math Clip Art--Geometry Concepts--Scale Drawing--07 | Math Clip Art--Scale Drawing--07TopicGeometry Concepts DescriptionThis image depicts a scale drawing of a right triangle that has been scaled down by a factor of 3:1. Each side of the triangle in the drawing is one-third the length of the corresponding side in the actual object. Scaling down is useful for creating manageable representations of larger objects. Teacher's Script: "Examine this scale drawing of a right triangle. How does the 3:1 scale factor help us understand the relationship between the drawing and the actual triangle? What are some real-world applications of scaling down objects, such as in model making or map creation?" |
Proportions |
|
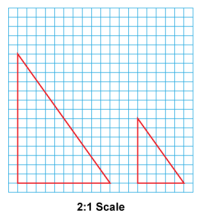
Math Clip Art--Geometry Concepts--Scale Drawing--08 | Math Clip Art--Scale Drawing--08TopicGeometry Concepts DescriptionThis image illustrates a scale drawing of a right triangle that has been scaled down by a factor of 2:1. Each side of the triangle in the drawing is one-half the length of the corresponding side in the actual object. This scaling helps in visualizing smaller versions of objects while maintaining accurate proportions. Teacher's Script: "Observe this scale drawing of a right triangle. How does the 2:1 scale factor affect the dimensions of the drawing compared to the actual triangle? What are some mathematical concepts you can explore using scale drawings, such as ratios or proportions?" |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 01 | Math Clip Art--Ratios, Proportions, Percents--Proportions 01TopicRatios, Proportions, and Percents DescriptionThis image showcases the concept of proportions using a dynamic visual of a runner in action framed within a golden ratio spiral. The proportion is represented algebraically as a/b = c/d, linking visual and mathematical representations. It introduces proportions conceptually and visually, setting the foundation for the subsequent examples. |
Proportions |
|
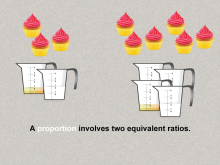
Math Clip Art--Ratios, Proportions, Percents--Proportions 02 | Math Clip Art--Ratios, Proportions, Percents--Proportions 02TopicRatios, Proportions, and Percents DescriptionThis image illustrates proportions using two equivalent ratios, represented by measuring cups and cupcakes. It simplifies proportions to relatable everyday examples. It connects proportions to practical examples, emphasizing the real-world relevance. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 03 | Math Clip Art--Ratios, Proportions, Percents--Proportions 03TopicRatios, Proportions, and Percents DescriptionThis image uses coins to demonstrate proportions. The image compares groups of quarters and nickels to highlight equivalent ratios (3:1 and 6:2). It solidifies the concept of equivalent ratios through another real-life example, reinforcing the idea. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 04 | Math Clip Art--Ratios, Proportions, Percents--Proportions 04TopicRatios, Proportions, and Percents DescriptionThis image demonstrates proportions through a scale model example, comparing the height and width ratios of the Eiffel Tower in two scales. It highlights the application of proportions in scaling and models, bridging abstract and practical understanding. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
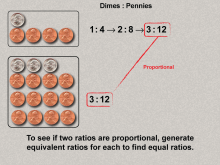
Math Clip Art--Ratios, Proportions, Percents--Proportions 05 | Math Clip Art--Ratios, Proportions, Percents--Proportions 05TopicRatios, Proportions, and Percents DescriptionThis image shows proportionality between dimes and pennies using equivalent ratios (1:4 and 3:12). Mathematical steps verify proportionality. It introduces proportional reasoning and calculation steps to ensure clarity in identifying proportional relationships. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
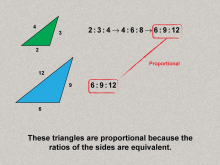
Math Clip Art--Ratios, Proportions, Percents--Proportions 06 | Math Clip Art--Ratios, Proportions, Percents--Proportions 06TopicRatios, Proportions, and Percents DescriptionThis image presents proportional triangles, with side lengths maintaining equivalent ratios (2:3:4 and 6:9:12). It demonstrates geometric applications of proportions, extending the concept to shapes and measurements. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 07 | Math Clip Art--Ratios, Proportions, Percents--Proportions 07TopicRatios, Proportions, and Percents DescriptionThis image contrasts proportionality with non-proportional groups of coins (dimes and nickels). Ratios differ, clarifying when proportions do not exist. It explains non-proportionality to deepen understanding of proportional relationships. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
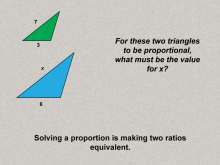
Math Clip Art--Ratios, Proportions, Percents--Proportions 08 | Math Clip Art--Ratios, Proportions, Percents--Proportions 08TopicRatios, Proportions, and Percents DescriptionThis image poses a question about proportional triangles, asking for the missing value (x) to maintain proportionality. It introduces problem-solving involving proportions, encouraging engagement and application. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
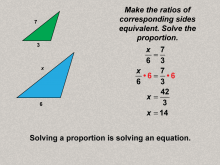
Math Clip Art--Ratios, Proportions, Percents--Proportions 09 | Math Clip Art--Ratios, Proportions, Percents--Proportions 09TopicRatios, Proportions, and Percents DescriptionThis image solves the posed proportion problem by finding the value of x using equivalent ratios (x/6 = 7/3). It breaks down the process of solving proportions, reinforcing mathematical reasoning. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Proportions 10 | Math Clip Art--Ratios, Proportions, Percents--Proportions 10TopicRatios, Proportions, and Percents DescriptionThis image demonstrates proportionality in coins by calculating the number of nickels required for proportional groups (2/5 = 6/x). It closes the sequence with a real-world problem, consolidating the topic and providing a practical application. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
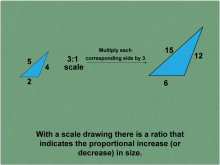
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
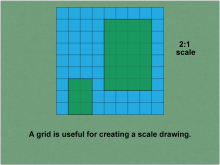
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |

|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
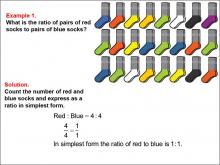
|
Math Example--Ratios and Rates--Example 1 | Math Example--Ratios and Rates--Example 1TopicRatios and Rates DescriptionThis math example focuses on understanding ratios using colored socks. The image displays a collection of red and blue socks, and students are asked to determine the ratio of red socks to blue socks. The solution demonstrates that there are 4 pairs of red socks and 4 pairs of blue socks, resulting in a ratio of 4 : 4, which simplifies to 1 : 1. |
Ratios and Rates |
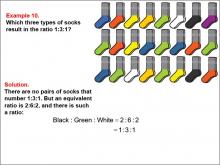
|
Math Example--Ratios and Rates--Example 10 | Math Example--Ratios and Rates--Example 10TopicRatios and Rates DescriptionThis example focuses on finding equivalent ratios using a collection of socks in various colors. The image shows socks arranged in rows, with black, green, white, and other colors present. Students are asked to find a ratio among three colors that is equivalent to 1 : 3 : 1. |
Ratios and Rates |
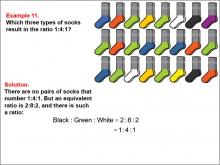
|
Math Example--Ratios and Rates--Example 11 | Math Example--Ratios and Rates--Example 11TopicRatios and Rates DescriptionThis example focuses on finding equivalent ratios using a collection of socks in various colors. The image shows socks arranged in rows, with black, green, white, and other colors present. Students are asked to find a ratio among three colors that is equivalent to 1 : 4 : 1. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 12 | Math Example--Ratios and Rates--Example 12TopicRatios and Rates DescriptionThis example explores the concept of similar triangles using ratios. The image shows a right triangle with sides labeled as 9, 12, and 15 units. Students are asked to determine if this triangle is similar to a standard 3-4-5 Pythagorean triplet triangle. Understanding similar triangles is an important application of ratios in geometry. This example demonstrates how ratios can be used to compare the sides of triangles and determine similarity. By scaling the sides of a known triangle (3-4-5) and comparing them to the given triangle, students can see how ratios maintain proportionality in similar shapes. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 13 | Math Example--Ratios and Rates--Example 13TopicRatios and Rates DescriptionThis example focuses on verifying the similarity of triangles using ratios. The image shows a right triangle with sides labeled 25, 60, and 65 units. Students are guided through a step-by-step process to determine if this triangle is similar to a 5-12-13 right triangle. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 14 | Math Example--Ratios and Rates--Example 14TopicRatios and Rates DescriptionThis example explores the concept of special right triangles using ratios. The image shows a right triangle with sides labeled 3, 3 2 2 , and 6 units. Students are guided through a step-by-step process to verify if this triangle is similar to a 30°-60°-90° triangle. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 15 | Math Example--Ratios and Rates--Example 15TopicRatios and Rates |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 16 | Math Example--Ratios and Rates--Example 16TopicRatios and Rates DescriptionThis example focuses on converting units of speed and calculating rates. The image shows a car and calculations for converting speed from miles per hour to feet per second, given the distance traveled in miles and time in minutes. Understanding unit conversions and rate calculations is crucial in many real-world applications, particularly in physics and engineering. This example demonstrates how to use ratios to convert between different units of speed, showcasing the practical application of mathematical concepts in everyday scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 17 | Math Example--Ratios and Rates--Example 17TopicRatios and Rates DescriptionThis example explores the concept of unit rates using the cost of gasoline. The image shows a red gasoline container, and students are asked to calculate the cost per gallon of gas given the total cost and volume. Understanding unit rates is a fundamental skill in mathematics with numerous real-world applications. This example demonstrates how to calculate a unit rate by dividing the total cost by the total quantity, illustrating the practical use of division in everyday scenarios like purchasing gasoline. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 18 | Math Example--Ratios and Rates--Example 18TopicRatios and Rates DescriptionThis example focuses on calculating unit rates in a restaurant context. The image shows a hamburger, and students are asked to determine the cost per pound of ground beef given the total cost and weight purchased. Understanding unit rates is essential in various real-world scenarios, particularly in business and economics. This example illustrates how to calculate a unit rate by dividing the total cost by the total quantity, demonstrating the practical application of division in a restaurant supply context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 19 | Math Example--Ratios and Rates--Example 19TopicRatios and Rates DescriptionThis example explores the concept of flow rates using a backyard pool scenario. The image shows a backyard pool, and students are asked to calculate the rate of water flow in gallons per minute given the pool's capacity and the time taken to fill it. Understanding flow rates is important in various fields, including engineering and physics. This example demonstrates how to calculate a rate by dividing the total volume by the total time, illustrating the practical application of division in real-world scenarios involving fluid dynamics. |
Ratios and Rates |
|
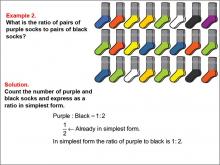
Math Example--Ratios and Rates--Example 2 | Math Example--Ratios and Rates--Example 2TopicRatios and Rates DescriptionThis example explores ratios using purple and black socks. The image shows a collection of socks, and students are asked to determine the ratio of purple socks to black socks. The solution reveals that there is 1 pair of purple socks and 2 pairs of black socks, resulting in a ratio of 1 : 2, which is already in its simplest form. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 20 | Math Example--Ratios and Rates--Example 20TopicRatios and Rates DescriptionThis example focuses on unit conversion using the height of the Statue of Liberty. The image shows the Statue of Liberty, and students are asked to convert its height from feet to inches. Understanding unit conversions is crucial in many fields, including science, engineering, and everyday life. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in real-world measurement scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 21 | Math Example--Ratios and Rates--Example 21TopicRatios and Rates DescriptionThis example focuses on unit conversion, specifically converting the height of the Statue of Liberty from feet to yards. The image shows the iconic Statue of Liberty, providing a real-world context for the mathematical problem. Understanding unit conversions is crucial in many fields, including engineering, science, and everyday life. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of division and multiplication in real-world measurement scenarios. |
Ratios and Rates |