
Illustrative Math Alignment: Grade 7 Unit 2
Introducing Proportional Relationships
Lesson 10: Introducing Graphs of Proportional Relationships
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Lesson Plan Collection: Ratios, Proportions, and Percents (Gr 7) | Ratios, Proportions, and Percents (Gr. 7) | 5-Lesson Unit This comprehensive collection of Grade 7 math lessons focuses on developing students’ understanding of ratios, proportions, and percents through real-world applications and multi-step problem-solving strategies. Each lesson is designed to build critical thinking skills and reinforce proportional reasoning, preparing students for more advanced mathematical concepts. Topics in this collection include: |
Ratios and Rates, Applications of Ratios, Proportions, and Percents, Proportions and Applications of Linear Functions |

|
Lesson Plan Collection: Ratios, Proportions, and Percents (Gr 7) | Ratios, Proportions, and Percents (Gr. 7) | 5-Lesson Unit This comprehensive collection of Grade 7 math lessons focuses on developing students’ understanding of ratios, proportions, and percents through real-world applications and multi-step problem-solving strategies. Each lesson is designed to build critical thinking skills and reinforce proportional reasoning, preparing students for more advanced mathematical concepts. Topics in this collection include: |
Ratios and Rates, Applications of Ratios, Proportions, and Percents, Proportions and Applications of Linear Functions |
|
Math Video Definitions Collection: Linear Functions | OverviewThis collection of math videos on Linear Functions provides comprehensive definitions for key concepts related to linear functions, equations, and graphs. Designed to enhance math instruction, these videos introduce essential vocabulary to support a deeper understanding of the topic. The collection covers a variety of terms and concepts, including slope, y-intercept, linear equations, and more, making it a valuable resource for building foundational skills in algebra. |
Slope-Intercept Form, Applications of Linear Functions, Graphs of Linear Functions, Point-Slope Form, Slope, Standard Form, Solving Systems of Equations, Proportions, Data Analysis, Variable Expressions, Functions and Their Inverses, Special Functions, Polynomial Expressions and Numerical Expressions |

|
Lesson Plan Collection: Ratios, Proportions, and Percents (Gr 7) | Ratios, Proportions, and Percents (Gr. 7) | 5-Lesson Unit This comprehensive collection of Grade 7 math lessons focuses on developing students’ understanding of ratios, proportions, and percents through real-world applications and multi-step problem-solving strategies. Each lesson is designed to build critical thinking skills and reinforce proportional reasoning, preparing students for more advanced mathematical concepts. Topics in this collection include: |
Ratios and Rates, Applications of Ratios, Proportions, and Percents, Proportions and Applications of Linear Functions |

|
Math Definitions Collection: Geometry | OverviewThe Geometry Basics collection from Media4Math is an essential resource for educators looking to enhance their students' understanding of fundamental geometric concepts. This comprehensive set includes 58 terms, each presented as a downloadable PNG image card that can be seamlessly integrated into classroom presentations. |
Definition of an Angle, Geometric Constructions with Points and Lines, 3-Dimensional Figures, Exploring Coordinate Systems, Definition of a Triangle, Definition of a Point, Definition of a Circle, Definition of Transformations, The Distance Formula, Definition of a Polygon, Definition of a Plane, Definition of a Line, Midpoint Formula, Applications of Polygons, Area and Perimeter of Triangles, Area and Perimeter of Quadrilaterals, Pyramids, Trig Expressions and Identities, Right Triangles, Definition of a Quadrilateral, Applications of Points and Lines and Proportions |

|
Math Definitions Collection: Ratios, Proportions, and Percents | OverviewThis collection of definitions on the topic of Ratios, Proportions, and Percents from Media4Math is an invaluable educational resource designed to enhance students' understanding of these fundamental mathematical concepts. This comprehensive collection includes essential terms such as ratio, proportion, percent, rate, unit rate, and scale model. |
Applications of Ratios, Proportions, and Percents, Ratios and Rates, Percents and Proportions |

|
Math Definitions Collection: Ratios, Proportions, and Percents | OverviewThis collection of definitions on the topic of Ratios, Proportions, and Percents from Media4Math is an invaluable educational resource designed to enhance students' understanding of these fundamental mathematical concepts. This comprehensive collection includes essential terms such as ratio, proportion, percent, rate, unit rate, and scale model. |
Applications of Ratios, Proportions, and Percents, Ratios and Rates, Percents and Proportions |

|
Math Definitions Collection: Ratios, Proportions, and Percents | OverviewThis collection of definitions on the topic of Ratios, Proportions, and Percents from Media4Math is an invaluable educational resource designed to enhance students' understanding of these fundamental mathematical concepts. This comprehensive collection includes essential terms such as ratio, proportion, percent, rate, unit rate, and scale model. |
Applications of Ratios, Proportions, and Percents, Ratios and Rates, Percents and Proportions |

|
Math Clip Art Collection: Geometry Concepts | OverviewThis collection of math clip art on Geometry Concepts contains over 100 resources that provide a visual and interactive way to teach geometric concepts. Math clip art is an invaluable tool for teachers, as it allows them to create visually appealing and informative materials that capture students' attention and reinforce key concepts. This collection is particularly useful for elementary math instruction, offering a wide range of ten frame models that can be easily incorporated into lessons, worksheets, and pres |
Surface Area, Applications of Transformations, Definition of a Circle, Applications of Polygons, Modeling Shapes, 3-Dimensional Figures, Applications of 3D Geometry, Exploring Coordinate Systems, Coordinate Systems, Applications of Coordinate Geometry, Applications of Points and Lines, Definition of a Quadrilateral, Applications of Triangles, Numerical Expressions, Geometric Constructions with Angles and Planes, Geometric Constructions with Points and Lines, Length, Definition of a Polygon, Definition of a Triangle, Exponential and Logarithmic Functions and Equations, Graphs of Exponential and Logarithmic Functions, Parallel Lines, Perpendicular Lines, Identifying Shapes, Proportions, Applications of Quadrilaterals and Geometric Constructions with Polygons |

|
Math Definitions Collection: Geometry | OverviewThe Geometry Basics collection from Media4Math is an essential resource for educators looking to enhance their students' understanding of fundamental geometric concepts. This comprehensive set includes 58 terms, each presented as a downloadable PNG image card that can be seamlessly integrated into classroom presentations. |
Definition of an Angle, Geometric Constructions with Points and Lines, 3-Dimensional Figures, Exploring Coordinate Systems, Definition of a Triangle, Definition of a Point, Definition of a Circle, Definition of Transformations, The Distance Formula, Definition of a Polygon, Definition of a Plane, Definition of a Line, Midpoint Formula, Applications of Polygons, Area and Perimeter of Triangles, Area and Perimeter of Quadrilaterals, Pyramids, Trig Expressions and Identities, Right Triangles, Definition of a Quadrilateral, Applications of Points and Lines and Proportions |

|
Math Tutorials Collection: Applications of Linear Functions |
OverviewThis collection aggregates a set of tutorials on Applications of Linear Functions. There are a total of 10 tutorials. |
Applications of Linear Functions and Proportions |

|
Instructional Resource Collection: The Fibonacci Sequence |
OverviewThis is a collection of lessons on the Fibonacci Sequence. There are six lessons.
|
Sequences, Exploring Coordinate Systems, Applications of Exponential and Logarithmic Functions, Ratios and Rates, Proportions, Geometric Constructions with Triangles and Applications of Quadrilaterals |

|
Math Clip Art Collection: Geometry Concepts | OverviewThis collection of math clip art on Geometry Concepts contains over 100 resources that provide a visual and interactive way to teach geometric concepts. Math clip art is an invaluable tool for teachers, as it allows them to create visually appealing and informative materials that capture students' attention and reinforce key concepts. This collection is particularly useful for elementary math instruction, offering a wide range of ten frame models that can be easily incorporated into lessons, worksheets, and pres |
Surface Area, Applications of Transformations, Definition of a Circle, Applications of Polygons, Modeling Shapes, 3-Dimensional Figures, Applications of 3D Geometry, Exploring Coordinate Systems, Coordinate Systems, Applications of Coordinate Geometry, Applications of Points and Lines, Definition of a Quadrilateral, Applications of Triangles, Numerical Expressions, Geometric Constructions with Angles and Planes, Geometric Constructions with Points and Lines, Length, Definition of a Polygon, Definition of a Triangle, Exponential and Logarithmic Functions and Equations, Graphs of Exponential and Logarithmic Functions, Parallel Lines, Perpendicular Lines, Identifying Shapes, Proportions, Applications of Quadrilaterals and Geometric Constructions with Polygons |

|
Math in the News Collection: Applications of Ratios |
OverviewThis is a collection of Math in the News stories that focus on the topic of Ratios, Proportions, and Percents.
|
Applications of Ratios, Proportions, and Percents and Proportions |

|
Math Clip Art Collection: Geometry Concepts | OverviewThis collection of math clip art on Geometry Concepts contains over 100 resources that provide a visual and interactive way to teach geometric concepts. Math clip art is an invaluable tool for teachers, as it allows them to create visually appealing and informative materials that capture students' attention and reinforce key concepts. This collection is particularly useful for elementary math instruction, offering a wide range of ten frame models that can be easily incorporated into lessons, worksheets, and pres |
Surface Area, Applications of Transformations, Definition of a Circle, Applications of Polygons, Modeling Shapes, 3-Dimensional Figures, Applications of 3D Geometry, Exploring Coordinate Systems, Coordinate Systems, Applications of Coordinate Geometry, Applications of Points and Lines, Definition of a Quadrilateral, Applications of Triangles, Numerical Expressions, Geometric Constructions with Angles and Planes, Geometric Constructions with Points and Lines, Length, Definition of a Polygon, Definition of a Triangle, Exponential and Logarithmic Functions and Equations, Graphs of Exponential and Logarithmic Functions, Parallel Lines, Perpendicular Lines, Identifying Shapes, Proportions, Applications of Quadrilaterals and Geometric Constructions with Polygons |

|
Algebra Applications: Dinosaur Footprints | Algebra Applications: Dinosaur Footprints
Paleontologists rely on fossils to learn about dinosaurs. They also rely on certain algebraic concepts to help them estimate the sizes of dinosaurs based on the measurements of dinosaur footprints. In this activity, walk students through the solution of several proportions to estimate the sizes of different dinosaurs. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Proportions |

|
Algebra Applications: Dinosaur Footprints | Algebra Applications: Dinosaur Footprints
Paleontologists rely on fossils to learn about dinosaurs. They also rely on certain algebraic concepts to help them estimate the sizes of dinosaurs based on the measurements of dinosaur footprints. In this activity, walk students through the solution of several proportions to estimate the sizes of different dinosaurs. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Proportions |

|
Algebra Applications: Dinosaur Footprints | Algebra Applications: Dinosaur Footprints
Paleontologists rely on fossils to learn about dinosaurs. They also rely on certain algebraic concepts to help them estimate the sizes of dinosaurs based on the measurements of dinosaur footprints. In this activity, walk students through the solution of several proportions to estimate the sizes of different dinosaurs. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Proportions |

|
Closed Captioned Video: Linear Function | Closed Captioned Video: Linear Function
In this TI Nspire tutorial, the Graph window is used to graph a linear function. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. This is part of a collection of closed captioned videos on various math topics. To see the complete collection of the videos, click on this link. Note: The download is Media4Math's guide to closed captioned videos.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Video TranscriptsThis video has a transcript available. To see the complete collection of video transcripts, click on this link. |
Graphs of Linear Functions |

|
Closed Captioned Video: Linear Inequality Using Sliders | Closed Captioned Video: Linear Inequality Using Sliders
In this TI Nspire tutorial, the Graph window is used to graph a linear inequality in slope-intercept form using sliders. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. |
Inequalities |

|
Closed Captioned Video: Exp the Slope-Intercept form | Closed Captioned Video: Exp the Slope-Intercept form
In this TI Nspire tutorial, the Graph window is used to create a slider-based graph of a linear function in slope-intercept form. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. . |
Slope-Intercept Form |

|
Closed Captioned Video: Ratios and Proportions: What Are Proportions? | Closed Captioned Video: Ratios and Proportions: What Are Proportions?TopicRatios DescriptionProportions are explained as equivalent ratios used to solve real-world problems. Examples include matching juice mixtures and adjusting recipes. The video uses ratio tables and number lines to scale ratios proportionally in practical applications. |
Ratios and Rates |

|
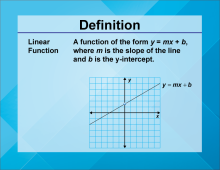
Definition--Direct Variation | Direct Variation
TopicLinear Functions DefinitionDirect variation describes a linear relationship between two variables where one variable is a constant multiple of the other, expressed as y = kx, where k is the constant of variation. DescriptionDirect variation is a fundamental concept in linear functions, illustrating how one variable changes proportionally with another. The constant of variation, 𝑘 k, represents the rate of change. In real-world scenarios, direct variation can model relationships such as speed and distance, where distance traveled varies directly with time at a constant speed. Understanding this concept is crucial in fields like physics and engineering. |
Applications of Linear Functions |
|
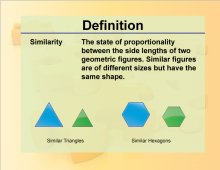
Definition--Geometry Basics--Similarity | SimilarityTopicGeometry Basics DefinitionSimilarity refers to figures that have the same shape but not necessarily the same size. DescriptionSimilarity is a key concept in geometry, used to compare shapes and solve problems involving proportions. For example, two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional. Understanding similarity helps in solving problems related to scaling, resizing, and geometric transformations. This concept is widely used in fields such as art, design, and architecture to create proportional and aesthetically pleasing structures. |
Proportions |

|
Definition--Geometry Basics--Similarity | SimilarityTopicGeometry Basics DefinitionSimilarity refers to figures that have the same shape but not necessarily the same size. DescriptionSimilarity is a key concept in geometry, used to compare shapes and solve problems involving proportions. For example, two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional. Understanding similarity helps in solving problems related to scaling, resizing, and geometric transformations. This concept is widely used in fields such as art, design, and architecture to create proportional and aesthetically pleasing structures. |
Proportions |

|
Definition--Geometry Basics--Similarity | SimilarityTopicGeometry Basics DefinitionSimilarity refers to figures that have the same shape but not necessarily the same size. DescriptionSimilarity is a key concept in geometry, used to compare shapes and solve problems involving proportions. For example, two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional. Understanding similarity helps in solving problems related to scaling, resizing, and geometric transformations. This concept is widely used in fields such as art, design, and architecture to create proportional and aesthetically pleasing structures. |
Proportions |

|
Definition--Geometry Basics--Similarity | SimilarityTopicGeometry Basics DefinitionSimilarity refers to figures that have the same shape but not necessarily the same size. DescriptionSimilarity is a key concept in geometry, used to compare shapes and solve problems involving proportions. For example, two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional. Understanding similarity helps in solving problems related to scaling, resizing, and geometric transformations. This concept is widely used in fields such as art, design, and architecture to create proportional and aesthetically pleasing structures. |
Proportions |

|
Definition--Geometry Basics--Similarity | SimilarityTopicGeometry Basics DefinitionSimilarity refers to figures that have the same shape but not necessarily the same size. DescriptionSimilarity is a key concept in geometry, used to compare shapes and solve problems involving proportions. For example, two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional. Understanding similarity helps in solving problems related to scaling, resizing, and geometric transformations. This concept is widely used in fields such as art, design, and architecture to create proportional and aesthetically pleasing structures. |
Proportions |

|
Definition--Geometry Basics--Similarity | SimilarityTopicGeometry Basics DefinitionSimilarity refers to figures that have the same shape but not necessarily the same size. DescriptionSimilarity is a key concept in geometry, used to compare shapes and solve problems involving proportions. For example, two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional. Understanding similarity helps in solving problems related to scaling, resizing, and geometric transformations. This concept is widely used in fields such as art, design, and architecture to create proportional and aesthetically pleasing structures. |
Proportions |

|
Definition--Geometry Basics--Similarity | SimilarityTopicGeometry Basics DefinitionSimilarity refers to figures that have the same shape but not necessarily the same size. DescriptionSimilarity is a key concept in geometry, used to compare shapes and solve problems involving proportions. For example, two triangles are similar if their corresponding angles are equal and their corresponding sides are proportional. Understanding similarity helps in solving problems related to scaling, resizing, and geometric transformations. This concept is widely used in fields such as art, design, and architecture to create proportional and aesthetically pleasing structures. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |
|
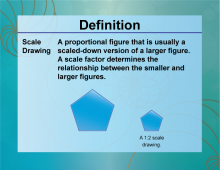
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Drawing | Scale DrawingTopicRatios, Proportions, and Percents DefinitionA scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure. DescriptionScale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Factor | Scale FactorTopicRatios, Proportions, and Percents DefinitionA scale factor is a number that scales, or multiplies, some quantity. DescriptionScale factors are used in various applications, such as resizing images, models, and maps. For instance, if a model car is built at a scale factor of 1:24, it means the model is 1/24th the size of the actual car. This concept is crucial in fields requiring accurate scaling, such as architecture and engineering. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Scale Factor | Scale FactorTopicRatios, Proportions, and Percents DefinitionA scale factor is a number that scales, or multiplies, some quantity. DescriptionScale factors are used in various applications, such as resizing images, models, and maps. For instance, if a model car is built at a scale factor of 1:24, it means the model is 1/24th the size of the actual car. This concept is crucial in fields requiring accurate scaling, such as architecture and engineering. |
Proportions |