
Illustrative Math Alignment: Grade 7 Unit 2
Introducing Proportional Relationships
Lesson 6: Using Equations to Solve Problems
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Example--Ratios and Rates--Example 26 | Math Example--Ratios and Rates--Example 26TopicRatios and Rates DescriptionThis example focuses on time unit conversion, specifically converting hours to minutes in the context of a standardized test duration. The image shows a clock, providing a visual representation of time for the mathematical problem. Understanding time unit conversions is crucial in many aspects of daily life, including scheduling, time management, and test-taking. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in time-related scenarios. |
Ratios and Rates |
|
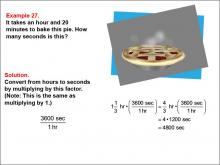
Math Example--Ratios and Rates--Example 27 | Math Example--Ratios and Rates--Example 27TopicRatios and Rates DescriptionThis example explores time unit conversion, specifically converting hours and minutes to seconds in the context of baking a pie. The image shows a steaming pie, providing a real-world scenario for the mathematical problem. Understanding time unit conversions, especially when dealing with mixed units, is important in various fields such as cooking, manufacturing, and project management. This example demonstrates how to use conversion factors to change units, illustrating the practical application of multiplication in time-related scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 28 | Math Example--Ratios and Rates--Example 28TopicRatios and Rates DescriptionThis example focuses on time unit conversion in a sports context, specifically converting minutes and seconds to seconds for a horse race lap time. The image shows a horse, providing a visual context for the mathematical problem. Understanding time unit conversions is crucial in many sports, especially those involving racing and timed events. This example demonstrates how to use conversion factors to change units and add different time units, illustrating the practical application of multiplication and addition in sports-related time scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 29 | Math Example--Ratios and Rates--Example 29TopicRatios and Rates DescriptionThis example explores time unit conversion in an IT context, specifically converting seconds to minutes for user session duration. The image shows a computer tower, providing a real-world scenario for the mathematical problem. Understanding time unit conversions is crucial in many technological fields, especially in IT and user experience analysis. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of division in time-related measurement scenarios. It also introduces the concept of mixed numbers in the result. |
Ratios and Rates |
|
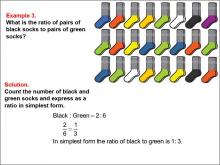
Math Example--Ratios and Rates--Example 3 | Math Example--Ratios and Rates--Example 3TopicRatios and Rates DescriptionThis example focuses on ratios using black and green socks. The image displays a collection of socks, and students are tasked with determining the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 6 pairs of green socks, resulting in a ratio of 2 : 6, which simplifies to 1 : 3. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 30 | Math Example--Ratios and Rates--Example 30TopicRatios and Rates DescriptionThis example focuses on time unit conversion in an IT context, specifically converting seconds to hours for user session duration. The image shows a computer tower, providing a real-world scenario for the mathematical problem. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 31 | Math Example--Ratios and Rates--Example 31TopicRatios and Rates DescriptionThis example focuses on temperature unit conversion, specifically converting Celsius to Fahrenheit for the boiling point of water. The image shows a beaker of boiling water, providing a visual context for the mathematical problem. Understanding temperature unit conversions is crucial in many scientific fields, including chemistry, physics, and meteorology. This example demonstrates how to use a conversion formula to change units, illustrating the practical application of mathematical equations in real-world temperature scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 32 | Math Example--Ratios and Rates--Example 32TopicRatios and Rates DescriptionThis example explores temperature unit conversion, specifically converting Fahrenheit to Celsius for the freezing point of water. The image shows icicles, providing a visual representation of the freezing temperature for the mathematical problem. |
Ratios and Rates |
|
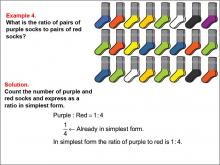
Math Example--Ratios and Rates--Example 4 | Math Example--Ratios and Rates--Example 4TopicRatios and Rates DescriptionThis example explores ratios using purple and red socks. The image shows a collection of socks, and students are asked to determine the ratio of purple socks to red socks. The solution reveals that there is 1 pair of purple socks and 4 pairs of red socks, resulting in a ratio of 1 : 4, which is already in its simplest form. |
Ratios and Rates |
|
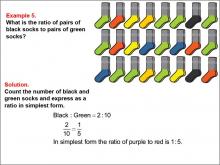
Math Example--Ratios and Rates--Example 5 | Math Example--Ratios and Rates--Example 5TopicRatios and Rates DescriptionThis example focuses on ratios using black and green socks among a variety of colored socks. The image displays pairs of socks in black, green, orange, yellow, blue, and red. Students are asked to determine the ratio of black socks to green socks. The solution shows that there are 2 pairs of black socks and 10 pairs of green socks, resulting in a ratio of 2 : 10, which simplifies to 1 : 5. |
Ratios and Rates |
|
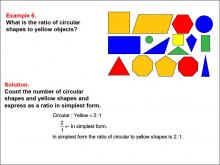
Math Example--Ratios and Rates--Example 6 | Math Example--Ratios and Rates--Example 6TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes of different colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of circular shapes to yellow objects. The solution reveals that there are 2 circular shapes and 1 yellow object, resulting in a ratio of 2 : 1, which is already in its simplest form. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 7 | Math Example--Ratios and Rates--Example 7TopicRatios and Rates DescriptionThis example focuses on ratios using geometric shapes. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of triangles to quadrilaterals. The solution shows that there are 4 triangles and 6 quadrilaterals, resulting in a ratio of 4 : 6, which simplifies to 2 : 3. |
Ratios and Rates |
|
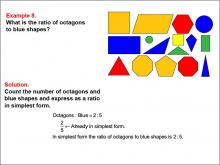
Math Example--Ratios and Rates--Example 8 | Math Example--Ratios and Rates--Example 8TopicRatios and Rates DescriptionThis example explores ratios using geometric shapes and colors. The image displays various shapes in yellow, blue, red, and green. Students are asked to determine the ratio of octagons to blue shapes. The solution reveals that there are 2 octagons and 5 blue shapes, resulting in a ratio of 2 : 5, which is already in its simplest form. |
Ratios and Rates |
|
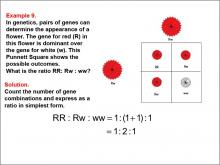
Math Example--Ratios and Rates--Example 9 | Math Example--Ratios and Rates--Example 9TopicRatios and Rates DescriptionThis example introduces the concept of ratios in genetics using a Punnett square. The image shows genetic combinations for a flower's color, including RR, Rw, and ww, with corresponding images of red and white flowers. Students are asked to determine the ratio of different gene combinations. |
Ratios and Rates |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1TopicRatios, Proportions, and Percents DescriptionThis example demonstrates how to solve a proportion problem where two ratios a:b and c:d are proportional. Given the values b = 3, c = 4, and d = 6, we need to find the value of a. The proportion is set up as a / 3 = 4 / 6, which is then solved to find that a = 2. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1TopicRatios, Proportions, and Percents DescriptionThis example demonstrates how to solve a proportion problem where two ratios a:b and c:d are proportional. Given the values b = 3, c = 4, and d = 6, we need to find the value of a. The proportion is set up as a / 3 = 4 / 6, which is then solved to find that a = 2. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar triangles with algebraic expressions. Two triangles are shown, one with sides of 6 and 9, and the other with sides of 2x and 2x + 9. The problem requires setting up a proportion: 6 / 9 = 2x / (2x + 9). Solving this equation leads to x = 9, which then allows us to find the side lengths of 18 and 27. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar triangles with algebraic expressions. Two triangles are shown, one with sides of 6 and 9, and the other with sides of 2x and 2x + 9. The problem requires setting up a proportion: 6 / 9 = 2x / (2x + 9). Solving this equation leads to x = 9, which then allows us to find the side lengths of 18 and 27. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, one with legs of 7 and 9, and the other with legs of 14 and x. The problem requires finding the length of side x by setting up a proportion based on the similar triangles: 7 / 9 = 14 / x. Solving this equation leads to x = 18. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, one with legs of 7 and 9, and the other with legs of 14 and x. The problem requires finding the length of side x by setting up a proportion based on the similar triangles: 7 / 9 = 14 / x. Solving this equation leads to x = 18. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, one with legs of 5 and 8, and the other with legs of 2x and (2x + 6). The problem requires setting up a proportion: 5 / 8 = 2x / (2x + 6). Solving this equation leads to x = 5, which then allows us to find the side lengths of 10 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, one with legs of 5 and 8, and the other with legs of 2x and (2x + 6). The problem requires setting up a proportion: 5 / 8 = 2x / (2x + 6). Solving this equation leads to x = 5, which then allows us to find the side lengths of 10 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°). Two triangles are shown, with the smaller one having sides of 6√3 and 6, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: (6√3) / 6 = x / 12. Solving this equation leads to x = 12√3. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°). Two triangles are shown, with the smaller one having sides of 6√3 and 6, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: (6√3) / 6 = x / 12. Solving this equation leads to x = 12√3. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°) and algebraic expressions. Two triangles are shown, with the smaller one having sides of 16 and 8, and the larger one having sides of (3x + 4) and 2x. The problem requires setting up a proportion: 16 / 8 = (3x + 4) / 2x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 8 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°) and algebraic expressions. Two triangles are shown, with the smaller one having sides of 16 and 8, and the larger one having sides of (3x + 4) and 2x. The problem requires setting up a proportion: 16 / 8 = (3x + 4) / 2x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 8 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the smaller one having sides of 4 and 3, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: 4 / 3 = x / 12. Solving this equation leads to x = 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the smaller one having sides of 4 and 3, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: 4 / 3 = x / 12. Solving this equation leads to x = 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the smaller one having sides of (3x + 4) and 6, and the larger one having sides of 3x and 3x. The problem requires setting up a proportion: 8 / 6 = (3x + 4) / 3x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 12 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the smaller one having sides of (3x + 4) and 6, and the larger one having sides of 3x and 3x. The problem requires setting up a proportion: 8 / 6 = (3x + 4) / 3x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 12 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 12 / 5 = x / 15. Solving this equation leads to x = 36. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 12 / 5 = x / 15. Solving this equation leads to x = 36. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of 10x + 8 and 5x. The problem requires setting up a proportion: 12 / 5 = (10x + 8) / 5x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 20 and 48. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of 10x + 8 and 5x. The problem requires setting up a proportion: 12 / 5 = (10x + 8) / 5x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 20 and 48. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 19 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 19TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar isosceles right triangles. Two 45-45-90 triangles are shown, with one having sides labeled y and 5√2, and the other having sides labeled x and 12. The problem requires finding the lengths of both x and y using the special properties of isosceles right triangles and proportions. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 19 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 19TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar isosceles right triangles. Two 45-45-90 triangles are shown, with one having sides labeled y and 5√2, and the other having sides labeled x and 12. The problem requires finding the lengths of both x and y using the special properties of isosceles right triangles and proportions. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 2 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 2TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion where b is expressed as x + 1, and c and d are given constants (c = 3, d = 2). The goal is to solve for a using the proportion a / b = c / d. By substituting the known values, we set up the equation a / (x + 1) = 3 / 2 and solve for a, resulting in the expression a = (3(x + 1)) / 2. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 2 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 2TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion where b is expressed as x + 1, and c and d are given constants (c = 3, d = 2). The goal is to solve for a using the proportion a / b = c / d. By substituting the known values, we set up the equation a / (x + 1) = 3 / 2 and solve for a, resulting in the expression a = (3(x + 1)) / 2. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 20 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 20TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar isosceles right triangles with algebraic expressions. Two 45-45-90 triangles are shown, with one having sides labeled 15√2 and 15, and the other having sides labeled √2 * 5x and y. The problem requires finding the length of y in terms of x using the special properties of isosceles right triangles and proportions. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 20 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 20TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar isosceles right triangles with algebraic expressions. Two 45-45-90 triangles are shown, with one having sides labeled 15√2 and 15, and the other having sides labeled √2 * 5x and y. The problem requires finding the length of y in terms of x using the special properties of isosceles right triangles and proportions. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 21 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 21TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar isosceles triangles. Two isosceles triangles are shown, with the smaller one having sides of 30 and 16, and the larger one having sides of x and 20. The problem requires finding the length of side x by setting up a proportion: 30 / 16 = x / 20. Solving this equation leads to x = 37.5. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 21 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 21TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar isosceles triangles. Two isosceles triangles are shown, with the smaller one having sides of 30 and 16, and the larger one having sides of x and 20. The problem requires finding the length of side x by setting up a proportion: 30 / 16 = x / 20. Solving this equation leads to x = 37.5. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 22 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 22TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar isosceles triangles with algebraic expressions. Two isosceles triangles are shown, with the smaller one having sides of 22 and 12, and the larger one having sides of 10x + 5 and 6x. The problem requires setting up a proportion: 22 / 12 = (10x + 5) / 6x. Solving this equation leads to x = 5, which then allows us to find the side lengths of the larger triangle. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 22 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 22TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar isosceles triangles with algebraic expressions. Two isosceles triangles are shown, with the smaller one having sides of 22 and 12, and the larger one having sides of 10x + 5 and 6x. The problem requires setting up a proportion: 22 / 12 = (10x + 5) / 6x. Solving this equation leads to x = 5, which then allows us to find the side lengths of the larger triangle. |
Proportions |
|
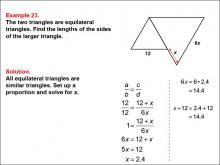
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 23 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 23TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar equilateral triangles. Two equilateral triangles are shown, with the smaller one having a side length of 12, and the larger one having a side length of 6x and an additional side labeled as 12 + x. The problem requires finding the lengths of the sides of the larger triangle by setting up a proportion: 12 / 12 = (12 + x) / 6x. Solving this equation leads to x = 2.4, and the length of the larger triangle's side is found to be approximately 14.4 units. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 23 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 23TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar equilateral triangles. Two equilateral triangles are shown, with the smaller one having a side length of 12, and the larger one having a side length of 6x and an additional side labeled as 12 + x. The problem requires finding the lengths of the sides of the larger triangle by setting up a proportion: 12 / 12 = (12 + x) / 6x. Solving this equation leads to x = 2.4, and the length of the larger triangle's side is found to be approximately 14.4 units. |
Proportions |
|
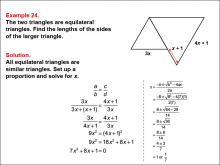
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 24 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 24TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a complex proportion problem using similar equilateral triangles with algebraic expressions. Two equilateral triangles are shown, with the smaller one having a side length of 3x, and the larger one having side lengths labeled as (4x + 1) and (x + 1). The problem requires setting up a proportion: 3x / (4x + 1) = 3x / (3x + (x + 1)). Solving this equation leads to a quadratic equation, which when solved gives x ≈ 7/1. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 24 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 24TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a complex proportion problem using similar equilateral triangles with algebraic expressions. Two equilateral triangles are shown, with the smaller one having a side length of 3x, and the larger one having side lengths labeled as (4x + 1) and (x + 1). The problem requires setting up a proportion: 3x / (4x + 1) = 3x / (3x + (x + 1)). Solving this equation leads to a quadratic equation, which when solved gives x ≈ 7/1. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 25 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 25TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar rectangles. Two rectangles are shown, with the smaller one having sides of 2 and 3, and the larger one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 2 / 3 = x / 15. Solving this equation leads to x = 10. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 25 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 25TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar rectangles. Two rectangles are shown, with the smaller one having sides of 2 and 3, and the larger one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 2 / 3 = x / 15. Solving this equation leads to x = 10. |
Proportions |