
Illustrative Math Alignment: Grade 7 Unit 3
Measuring Circles
Lesson 11: Stained-Glass Windows
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
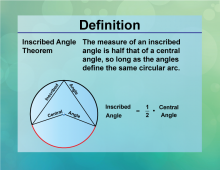
Definition--Circle Concepts--Inscribed Angle Theorem | Inscribed Angle TheoremTopicCircles DefinitionThe inscribed angle theorem states that an inscribed angle is half the measure of the central angle that subtends the same arc. |
Definition of a Circle |
|
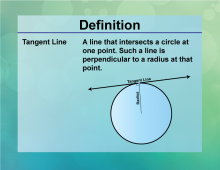
Definition--Circle Concepts--Tangent Line | Tangent LineTopicCircles DefinitionA tangent line is a straight line that touches a circle at exactly one point. |
Definition of a Circle |

|
Closed Captioned Video: Geometry Applications: Circles, 3 | Closed Captioned Video: Geometry Applications: Circles, 3TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. The video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
Closed Captioned Video: Geometry Applications: Circles, 3 | Closed Captioned Video: Geometry Applications: Circles, 3TopicCircles DescriptionFocusing on the Pantheon, this segment introduces chords, inscribed angles, and intercepted arcs, connecting them to architectural features. The video uses the oculus as a practical example, demonstrating how light patterns and angles relate to geometric principles. Applications include understanding light dynamics and their symbolic representation in architecture. |
Applications of Circles and Definition of a Circle |

|
Closed Captioned Video: Geometry Applications: Circles, 2 | Closed Captioned Video: Geometry Applications: Circles, 2TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Coliseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Coliseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
Closed Captioned Video: Geometry Applications: Circles, 2 | Closed Captioned Video: Geometry Applications: Circles, 2TopicCircles DescriptionThis segment explores the geometric complexities of the Roman Coliseum and its elliptical structure. It differentiates between circular and elliptical geometries, explaining terms like ellipse, foci, and perimeter. The video applies these concepts to analyze the construction techniques of the Coliseum, showcasing the Romans’ use of circular arcs to approximate an ellipse. |
Applications of Circles and Definition of a Circle |

|
Closed Captioned Video: Geometry Applications: Circles, 1 | Closed Captioned Video: Geometry Applications: Circles, 1TopicCircles DescriptionThis segment discusses the geometry of circles and their cultural and astronomical significance. It introduces concepts such as the center, radius, diameter, chords, and arcs, emphasizing their applications in ancient structures like Pueblo Bonito and Stonehenge. Key vocabulary includes equinox, solstice, radius, and chord. Applications include tracking celestial events and designing circular structures for ceremonial or observational purposes. |
Applications of Circles and Definition of a Circle |

|
Closed Captioned Video: Geometry Applications: Circles, 1 | Closed Captioned Video: Geometry Applications: Circles, 1TopicCircles DescriptionThis segment discusses the geometry of circles and their cultural and astronomical significance. It introduces concepts such as the center, radius, diameter, chords, and arcs, emphasizing their applications in ancient structures like Pueblo Bonito and Stonehenge. Key vocabulary includes equinox, solstice, radius, and chord. Applications include tracking celestial events and designing circular structures for ceremonial or observational purposes. |
Applications of Circles and Definition of a Circle |

|
Closed Captioned Video: Geometry Applications: Circles | Closed Captioned Video: Geometry Applications: CirclesTopicCircles |
Applications of Circles and Definition of a Circle |

|
Closed Captioned Video: Geometry Applications: Circles | Closed Captioned Video: Geometry Applications: CirclesTopicCircles |
Applications of Circles and Definition of a Circle |

|
Video Transcript: TI-Nspire Mini-Tutorial: Circumscribing a Circle about a Triangle | Video Transcript: TI-Nspire Mini-Tutorial: Circumscribing a Circle about a Triangle
This is the transcript for the TI-Nspire Mini-Tutorial entitled, Circumscribing a Circle about a Triangle. This is part of a collection of video transcripts for the video tutorial series on using the TI-Nspire Graphing Calculator. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. |
Geometric Constructions with Triangles |

|
Closed Captioned Video: Circumscribing a Circle-Triangle | Closed Captioned Video: Circumscribing a Circle-Triangle
In this TI Nspire tutorial, the Geometry window is used to circumscribe a circle about a triangle. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. . |
Geometric Constructions with Triangles |
|
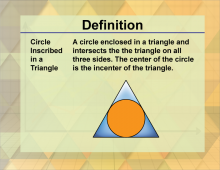
Definition--Triangle Concepts--Circle Inscribed In a Triangle | Circle Inscribed In a TriangleTopicTriangles DefinitionA circle inscribed in a triangle is a circle that touches all three sides of the triangle from the inside. DescriptionAn inscribed circle in a triangle, also known as an incircle, is a circle that is tangent to all three sides of the triangle. The center of this circle is called the incenter, which is the point where the angle bisectors of the triangle intersect. |
Definition of a Triangle |
|
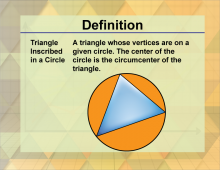
Definition--Triangle Concepts--Triangle Inscribed in a Circle | Triangle Inscribed in a CircleTopicTriangles DefinitionA triangle inscribed in a circle is a triangle whose vertices all lie on the circumference of the circle. DescriptionA triangle inscribed in a circle, also known as a circumtriangle, is a triangle whose vertices all lie on the circumference of the circle. The circle is called the circumcircle, and its center is the circumcenter of the triangle. |
Definition of a Triangle |

|
Definition--Polygon Concepts--Incircle | IncircleTopicPolygon Concepts DefinitionAn incircle is the largest circle that can be inscribed within a polygon, tangent to all of its sides. |
Definition of a Polygon |

|
Definition--Polygon Concepts--Circumscribed Circle | Circumscribed CircleDefinitionA circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter, and its radius is called the circumradius. |
Definition of a Polygon |

|
Instructional Resource: TI-Nspire Activity: Exploring the Ratio of Circumference to Radius as a Linear Function | In this TI-Nspire Activity, use the Geometry and Graphing Tools to explore the ratio of Circumference to Radius as a linear function. Note: The Preview is a Google Slide Show and the download is a PPT. Subscribers to Media4Math can download resources. To see the complete collection of TI graphing calculator resources, click on this Link. |
Applications of Linear Functions, Applications of Circles and Geometric Constructions with Circles |
|
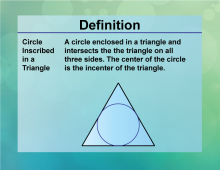
Definition--Circle Concepts--Circle Inscribed in a Triangle | Circle Inscribed in a TriangleTopicCircles DefinitionAn inscribed circle in a triangle is tangent to each of the triangle's sides. |
Definition of a Circle |
|
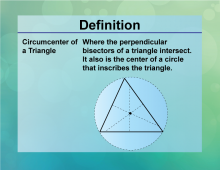
Definition--Circle Concepts--Circumcenter of Triangle | Circumcenter of TriangleTopicCircles DefinitionThe circumcenter of a triangle is the point where the perpendicular bisectors of the sides intersect, equidistant from the vertices. |
Definition of a Circle |
|
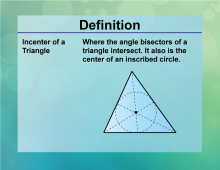
Definition--Circle Concepts--Incenter of a Triangle | Incenter of a TriangleTopicCircles DefinitionThe incenter of a triangle is the point where the angle bisectors intersect, equidistant from the sides. |
Definition of a Circle |
|
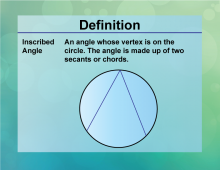
Definition--Circle Concepts--Inscribed Angle | Inscribed AngleTopicCircles DefinitionAn inscribed angle is an angle formed by two chords in a circle that share an endpoint. |
Definition of a Circle |
|
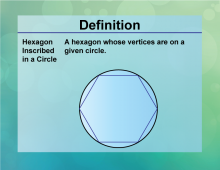
Definition--Circle Concepts--Hexagon Inscribed in a Circle | Hexagon Inscribed in a CircleTopicCircles DefinitionA hexagon inscribed in a circle is a six-sided polygon where each vertex touches the circle. |
Definition of a Circle |
|
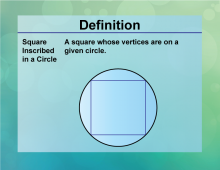
Definition--Circle Concepts--Square Inscribed in a Circle | Square Inscribed in a CircleTopicCircles DefinitionA square inscribed in a circle has its vertices touching the circle. |
Definition of a Circle |
|
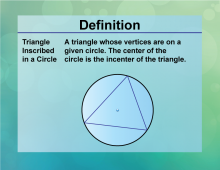
Definition--Circle Concepts--Triangle Inscribed in a Circle | Triangle Inscribed in a CircleTopicCircles DefinitionA triangle inscribed in a circle has its vertices on the circle. |
Definition of a Circle |
|
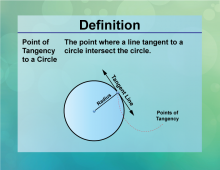
Definition--Circle Concepts--Point of Tangency to a Circle | Point of Tangency to a CircleTopicCircles DefinitionThe point of tangency is the point where a tangent line touches the circle. |
Definition of a Circle |

|
Definition--Circle Concepts--Concentric Circles | Concentric CirclesTopicCircles DefinitionConcentric circles are circles that share the same center but have different radii. |
Definition of a Circle |
|
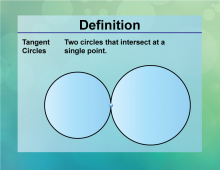
Definition--Circle Concepts--Tangent Circles | Tangent CirclesTopicCircles DefinitionTangent circles are two or more circles that intersect at exactly one point. |
Definition of a Circle |
|
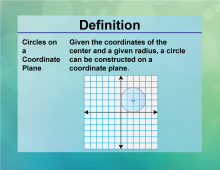
Definition--Circle Concepts--Circles on a Coordinate Plane | Circles on a Coordinate PlaneTopicCircles DefinitionCircles on a coordinate plane are defined by their center coordinates and radius. DescriptionUnderstanding circles on a coordinate plane is essential for analyzing geometric shapes in a mathematical context. This concept is widely used in computer graphics, navigation systems, and physics simulations, where precise positioning and movement of circular objects are required. The standard equation of a circle in the coordinate plane is (x − h)2 + (y − k)2 = r2 |
Definition of a Circle |
|
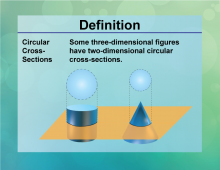
Definition--Circle Concepts--Circular Cross-Sections | Circular Cross-SectionsTopicCircles DefinitionCircular cross-sections are the intersections of a plane with a solid that result in a circle. |
Definition of a Circle |

|
Definition--Circle Concepts--Equation of a Circles | Equation of a CircleTopicCircles DefinitionThe equation of a circle in a plane is (x − h)2 + (y − k)2 = r2, where (h , k) is the center and r is the radius. |
Definition of a Circle |
|
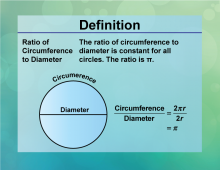
Definition--Circle Concepts--Ratio of Circumference to Diameter | Ratio of Circumference to DiameterTopicCircles DefinitionThe ratio of the circumference to the diameter of a circle is the constant π. |
Definition of a Circle |
|
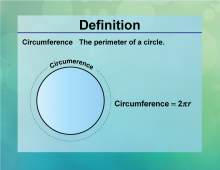
Definition--Circle Concepts--Circumference | CircumferenceTopicCircles DefinitionThe circumference of a circle is the distance around the circle, calculated as C = 2πr. DescriptionThe circumference is a fundamental concept in geometry, representing the perimeter of a circle. It is widely used in fields such as engineering, design, and manufacturing, where precise measurements of circular objects are required. The formula C = 2πr |
Definition of a Circle |
|
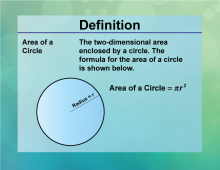
Definition--Circle Concepts--Area of a Circle | Area of a CircleTopicCircles DefinitionThe area of a circle is the space contained within its circumference, calculated as A = πr2 DescriptionThe area of a circle is a fundamental concept in geometry, representing the space enclosed by the circle's boundary. This concept is widely applicable in fields such as physics, engineering, and design, where understanding the area is crucial for tasks like calculating material quantities or designing circular components. The formula A = πr2 |
Definition of a Circle |

|
Definition--Circle Concepts--Circular Models | Circular ModelsTopicCircles DefinitionCircular models are representations of circular phenomena using mathematical equations and diagrams. |
Definition of a Circle |
|
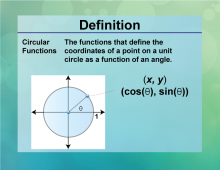
Definition--Circle Concepts--Circular Functions | Circular FunctionsTopicCircles DefinitionCircular functions are trigonometric functions that relate angles to ratios of sides in a right triangle. |
Definition of a Circle |
|
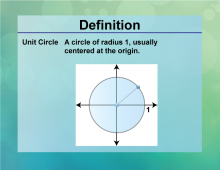
Definition--Circle Concepts--Unit Circle | Unit CircleTopicCircles DefinitionThe unit circle is a circle with a radius of one, centered at the origin of the coordinate plane. |
Definition of a Circle |
|
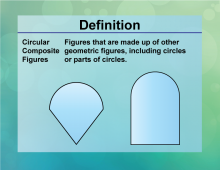
Definition--Circle Concepts--Circular Composite Figures | Circular Composite FiguresTopicCircles DefinitionCircular composite figures are shapes that include circles or parts of circles combined with other geometric figures. |
Definition of a Circle |
|
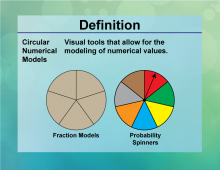
Definition--Circle Concepts--Circular Numerical Models | Circular Numerical ModelsTopicCircles DefinitionCircular numerical models use numerical methods to analyze and simulate circular phenomena. |
Definition of a Circle |

|
INSTRUCTIONAL RESOURCE: Algebra Application: Linear Functions: Circumference vs. Diameter | INSTRUCTIONAL RESOURCE: Algebra Application: Linear Functions: Circumference vs. Diameter
In this Algebra Application, students study the direction between diameter and circumference of a circle. Through measurement and data gathering students analyze the line of best fit and explore ways of calculating pi. The math topics covered include: Mathematical modeling, Linear functions, Data gathering and analysis, Ratios, Direct variation. This is a great back-to-school activity for middle school or high school students. This is also a great crossover activity that ties algebra and geometry. |
Applications of Linear Functions, Applications of Ratios, Proportions, and Percents and Applications of Circles |

|
Math in the News: Issue 118--The Return of the Orion | Math in the News: Issue 118 | The Return of the Orion
December 2022. In this issue of Math in the News we look at the Orion rocket's return to Earth from its lunar mission. This provides an opportunity to explore different types of orbits. —PRESS PREVIEW TO SEE THE SLIDE SHOW— This is part of the Math in the News collection. To see the complete collection, click on this link.Note: The download is a PPT file. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Circles |
|
Instructional Resource | Instructional Resource | Using the Unit Circle to Generate Trig Functions (Desmos)
In this tutorial, learn how to use the unit circle to generate trigonometric functions. —Click on Preview to see the tutorial— |
Trigonometric Functions |

|
Animated Math Clip Art--3D Geometry--Rotating a Circle to Form a Sphere | Rotating a Circle to Form a SphereTopic3D Geometry DescriptionThis animation demonstrates how rotating a circle around its diameter creates a sphere. It's a powerful visualization of how 2D shapes can generate 3D objects through rotation, illustrating a fundamental concept in solid geometry and calculus. Using animated math clip art like this helps students understand the relationship between 2D and 3D shapes, as well as the concept of solids of revolution. It bridges the gap between abstract mathematical concepts and visual representations, making complex ideas more accessible and engaging for learners. Teachers can use this animation to introduce or reinforce various mathematical concepts: |
3-Dimensional Figures |

|
Math Clip Art--Applications of Direct Variations--Circles 1 | Math Clip Art--Applications of Direct Variations--Circles 1 This is a collection of clip art images that show an application of direction variations in the context of circles. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Direct Variations--Circles 1 | Math Clip Art--Applications of Direct Variations--Circles 1 This is a collection of clip art images that show an application of direction variations in the context of circles. |
Ratios and Rates and Proportions |
|
Math Clip Art--Applications of Direct Variations--Circles 2 | Math Clip Art--Applications of Direct Variations--Circles 2 This is a collection of clip art images that show an application of direction variations in the context of circles. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Direct Variations--Circles 2 | Math Clip Art--Applications of Direct Variations--Circles 2 This is a collection of clip art images that show an application of direction variations in the context of circles. |
Ratios and Rates and Proportions |
|
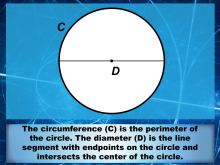
Math Clip Art--Applications of Direct Variations--Circles 3 | Math Clip Art--Applications of Direct Variations--Circles 3 This is a collection of clip art images that show an application of direction variations in the context of circles. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Direct Variations--Circles 3 | Math Clip Art--Applications of Direct Variations--Circles 3 This is a collection of clip art images that show an application of direction variations in the context of circles. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Direct Variations--Circles 4 | Math Clip Art--Applications of Direct Variations--Circles 4 This is a collection of clip art images that show an application of direction variations in the context of circles. |
Ratios and Rates and Proportions |

|
Math Clip Art--Applications of Direct Variations--Circles 4 | Math Clip Art--Applications of Direct Variations--Circles 4 This is a collection of clip art images that show an application of direction variations in the context of circles. |
Ratios and Rates and Proportions |