
Illustrative Math Alignment: Grade 7 Unit 5
Rational Number Arithmetic
Lesson 11: Dividing Rational Numbers
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topics |
|---|---|---|---|

|
VIDEO: Algebra Applications: Rational Functions | VIDEO: Algebra Applications: Rational Functions
TopicRational Functions |
Rational Expressions and Rational Functions and Equations |

|
Animated Math Clip Art--Rational Expressions 1 | This is part of a series of animated math clip art images that show that shows different rational expressions. Use these animated GIFs in PowerPoint, Google Slides, and Media4Math's proprietary Slide Show Creator. | Rational Expressions |

|
Animated Math Clip Art--Rational Expressions 2 | This is part of a series of animated math clip art images that show that shows different rational expressions. Use these animated GIFs in PowerPoint, Google Slides, and Media4Math's proprietary Slide Show Creator. | Rational Expressions |

|
Animated Math Clip Art--Rational Expressions 3 | This is part of a series of animated math clip art images that show that shows different rational expressions. Use these animated GIFs in PowerPoint, Google Slides, and Media4Math's proprietary Slide Show Creator. | Rational Expressions |
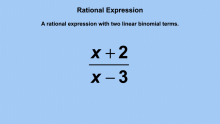
|
Animated Math Clip Art--Rational Expressions 4 | This is part of a series of animated math clip art images that show that shows different rational expressions. Use these animated GIFs in PowerPoint, Google Slides, and Media4Math's proprietary Slide Show Creator. | Rational Expressions |

|
Animated Math Clip Art--Rational Expressions 5 | This is part of a series of animated math clip art images that show that shows different rational expressions. Use these animated GIFs in PowerPoint, Google Slides, and Media4Math's proprietary Slide Show Creator. | Rational Expressions |

|
Animated Math Clip Art--Rational Expressions 6 | This is part of a series of animated math clip art images that show that shows different rational expressions. Use these animated GIFs in PowerPoint, Google Slides, and Media4Math's proprietary Slide Show Creator. | Rational Expressions |

|
Animated Math Clip Art--Rational Expressions 7 | This is part of a series of animated math clip art images that show that shows different rational expressions. Use these animated GIFs in PowerPoint, Google Slides, and Media4Math's proprietary Slide Show Creator. | Rational Expressions |

|
Closed Captioned Video: Adding-Subtracting Rational Exp | Closed Captioned Video: Adding-Subtracting Rational Exp
In this TI Nspire tutorial for the TI-Nspire CAS, the Calculator Window is used to combine and simplify rational expressions. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. . |
Rational Expressions |

|
Closed Captioned Video: Algebra Applications: Rational Functions | Closed Captioned Video: Algebra Applications: Rational FunctionsTopicRational Functions |
Rational Expressions and Rational Functions and Equations |

|
Closed Captioned Video: Algebra Applications: Rational Functions, 1 | Closed Captioned Video: Algebra Applications: Rational Functions, 1TopicRational Functions DescriptionExplains submarine pressure and volume relationships using rational functions, illustrating depth impacts on vessel integrity and scuba safety. This video provides a detailed explanation of explains submarine pressure and volume relationships using rational functions, illustrating depth impacts on vessel integrity and scuba safety. and its significance in understanding rational functions. |
Rational Expressions and Rational Functions and Equations |

|
Closed Captioned Video: Algebra Applications: Rational Functions, 2 | Closed Captioned Video: Algebra Applications: Rational Functions, 2TopicRational Functions DescriptionExamines surface area to volume ratios in animals using rational functions, connecting these ratios to evolutionary adaptations in different climates. This video provides a detailed explanation of examines surface area to volume ratios in animals using rational functions, connecting these ratios to evolutionary adaptations in different climates and its significance in understanding rational functions. |
Rational Expressions and Rational Functions and Equations |

|
Closed Captioned Video: Algebra Applications: Rational Functions, 3 | Closed Captioned Video: Algebra Applications: Rational Functions, 3TopicRational Functions DescriptionDemonstrates the optics of the Hubble telescope through rational functions, analyzing lens properties and asymptotes for image clarity. This video provides a detailed explanation of demonstrates the optics of the Hubble telescope through rational functions, analyzing lens properties and asymptotes for image clarity and its significance in understanding rational functions. |
Rational Expressions and Rational Functions and Equations |

|
Closed Captioned Video: Algebra Nspirations: Rational Functions | Closed Captioned Video: Algebra Nspirations: Rational Functions and Expressions
After briefly reviewing the concept of inverse variation, this video explores Boyle’s law, a real world example of an inversely proportional relationship between pressure and volume of a gas. Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, it goes on to examine similarities and differences among rational functions and numbers. Finally, it takes a look at rational functions graphs and ends with a delightful example merging Euclidean and analytic geometry, thanks to the TI-Nspire technology. Concepts explored: functions, rational expressions, rational functions, asymptotes |
Rational Expressions and Rational Functions and Equations |

|
Closed Captioned Video: Algebra Nspirations: Rational Functions, 1 | Closed Captioned Video: Algebra Nspirations: Rational Functions and Expressions, Segment 1
In this Investigation we look at an application of rational functions: Boyle's Law. This video is Segment 1 of a 4 segment series related to Algebra Nspirations: Rational Functions and Expressions. Segments 1 and 2 are grouped together. |
Rational Expressions and Rational Functions and Equations |
|
Closed Captioned Video: Algebra Nspirations: Rational Functions, 3 | Closed Captioned Video: Algebra Nspirations: Rational Functions and Expressions, Segment 3
In this Investigation we look at graphs of rational functions. This video is Segment 3 of a 4 segment series related to Algebra Nspirations: Rational Functions and Expressions. Segments 3 and 4 are grouped together. |
Rational Expressions and Rational Functions and Equations |

|
Closed Captioned Video: Multiplying Rational Expressions | Closed Captioned Video: Multiplying Rational Expressions
In this TI Nspire tutorial for the TI-Nspire CAS, the Calculator Window is used to multiply rational expressions. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. . |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: Adding Rational Numbers | Closed Captioned Video: Rational Numbers: Adding Rational Numbers
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: Comparing and Ordering Rational Numbers | Closed Captioned Video: Rational Numbers: Comparing and Ordering Rational Numbers
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: Dividing Rational Numbers | Closed Captioned Video: Rational Numbers: Dividing Rational Numbers
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: Multiplying Rational Numbers | Closed Captioned Video: Rational Numbers: Multiplying Rational Numbers
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: Numerical Expressions with Rational Numbers | Closed Captioned Video: Rational Numbers: Numerical Expressions with Rational Numbers
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: Rational Numbers and Absolute Value | Closed Captioned Video: Rational Numbers: Rational Numbers and Absolute Value
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: Rational Numbers and Exponents | Closed Captioned Video: Rational Numbers: Rational Numbers and Exponents
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: Rational Numbers and Irrational Numbers | Closed Captioned Video: Rational Numbers: Rational Numbers and Irrational Numbers
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: Rational Numbers on a Number Line | Closed Captioned Video: Rational Numbers: Rational Numbers on a Number Line
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: Rational Numbers on the Cartesian Coordinate System | Closed Captioned Video: Rational Numbers: Rational Numbers on the Cartesian Coordinate System
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: Subtracting Rational Numbers | Closed Captioned Video: Rational Numbers: Subtracting Rational Numbers
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: Variable Expressions with Rational Numbers | Closed Captioned Video: Rational Numbers: Variable Expressions with Rational Numbers
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Rational Numbers: What Are Rational Numbers? | Closed Captioned Video: Rational Numbers: What Are Rational Numbers?
This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link.The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward. |
Rational Expressions |

|
Closed Captioned Video: Simplifying Rational Expressions | Closed Captioned Video: Simplifying Rational Expressions
In this TI Nspire tutorial for the TI-Nspire CAS, the Calculator Window is used to combine and simplify rational expressions. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. . |
Rational Expressions |
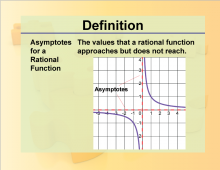
|
Definition--Rationals and Radicals--Asymptotes for a Rational Function | Asymptotes for a Rational FunctionTopicRationals and Radicals DefinitionAn asymptote is a line that a graph approaches but never touches. DescriptionAsymptotes are significant in the study of Rational Numbers, Expressions, Equations, and Functions. They help in understanding the behavior of graphs of rational functions, particularly as the values of the variables approach certain limits. Horizontal asymptotes indicate the value that the function approaches as the input grows infinitely large or small. Vertical asymptotes show the values that the function cannot take because they cause division by zero. |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Conjugate of a Radical | Conjugate of a RadicalTopicRationals and Radicals DefinitionThe conjugate of a radical expression is obtained by changing the sign between two terms in a binomial. DescriptionIn the context of Radical Numbers, Expressions, Equations, and Functions, the concept of conjugates is essential for simplifying expressions. When dealing with radicals, particularly in the denominator, multiplying by the conjugate can help to rationalize the expression. This process eliminates the radical from the denominator, making the expression easier to work with. |
Radical Expressions |

|
Definition--Rationals and Radicals--Cube Root | Cube RootTopicRationals and Radicals DefinitionThe cube root of a number is a value that, when multiplied by itself three times, gives the original number. DescriptionThe cube root is a fundamental concept in Radical Numbers, Expressions, Equations, and Functions. It is the inverse operation of raising a number to the power of three. Understanding cube roots is crucial for solving equations involving cubic terms and for simplifying radical expressions. Cube roots also appear in various real-world applications, such as calculating volumes and in certain physics equations. They are an integral part of higher-level mathematics, including algebra and calculus. |
Radical Expressions |

|
Definition--Rationals and Radicals--Extraneous Solution | Extraneous SolutionTopicRationals and Radicals DefinitionAn extraneous solution is a solution derived from an equation that is not a valid solution to the original equation. DescriptionExtraneous solutions often arise in the context of Rational and Radical Equations. They are solutions that appear during the process of solving an equation but do not satisfy the original equation. This can happen when both sides of an equation are squared or when other operations introduce additional solutions. |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Factoring a Radical | Factoring a RadicalTopicRationals and Radicals DefinitionFactoring a radical involves expressing it as a product of simpler expressions. DescriptionFactoring radicals is a key technique in the study of Radical Numbers, Expressions, Equations, and Functions. It simplifies complex radical expressions, making them easier to work with. This process is essential for solving equations and for performing algebraic manipulations involving radicals. Understanding how to factor radicals is also important for simplifying expressions in calculus and higher-level mathematics. It helps in breaking down complex problems into more manageable parts. |
Radical Functions and Equations |

|
Definition--Rationals and Radicals--Fourth Root | Fourth RootTopicRationals and Radicals DefinitionThe fourth root of a number is a value that, when raised to the power of four, gives the original number. DescriptionThe fourth root is an important concept in Radical Numbers, Expressions, Equations, and Functions. It is the inverse operation of raising a number to the power of four. Understanding fourth roots is crucial for solving higher-degree equations and for simplifying radical expressions. Fourth roots are also relevant in various scientific and engineering applications where higher-degree roots are required. They are a part of advanced mathematical studies, including algebra and calculus. |
Radical Expressions |

|
Definition--Rationals and Radicals--Geometric Mean | Geometric MeanTopicRationals and Radicals DefinitionThe geometric mean of two numbers is the square root of their product. DescriptionThe geometric mean is an example of using radical expressions to solve a problem. It provides a measure of central tendency that is particularly useful in situations where the numbers are multiplied together rather than added. In geometry, the geometric mean appears in various theorems and constructions. It is also used in finance and statistics to calculate average growth rates and to compare different sets of data. |
Radical Expressions |
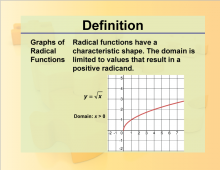
|
Definition--Rationals and Radicals--Graphs of Radical Functions | Graphs of Radical FunctionsTopicRationals and Radicals DefinitionGraphs of radical functions are visual representations of equations involving radicals. DescriptionGraphs of radical functions are crucial in the study of Radical Numbers, Expressions, Equations, and Functions. They provide a visual understanding of how these functions behave, including their domains, ranges, and key features such as intercepts and asymptotes. |
Radical Functions and Equations |
|
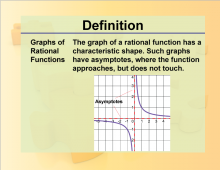
Definition--Rationals and Radicals--Graphs of Rational Functions | Graphs of Rational FunctionsTopicRationals and Radicals DefinitionGraphs of rational functions are visual representations of equations involving rational expressions. DescriptionGraphs of rational functions are fundamental in the study of Rational Numbers, Expressions, Equations, and Functions. They help in understanding the behavior of these functions, including their asymptotes, intercepts, and regions of increase and decrease. |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Horizontal Asymptote | Horizontal AsymptoteTopicRationals and Radicals DefinitionA horizontal asymptote is a horizontal line that a rational function graph approaches as the input values become very large or very small. DescriptionHorizontal asymptotes are an important concept in the study of Rational Numbers, Expressions, Equations, and Functions. They indicate the value that a function approaches as the input grows infinitely large or small. Understanding horizontal asymptotes is crucial for graphing rational functions accurately and for analyzing their long-term behavior. |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Inverse Variation | Inverse VariationTopicRationals and Radicals DefinitionInverse variation describes a relationship between two variables in which the product is a constant. When one variable increases, the other decreases proportionally. |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Irrational Number | Irrational NumberTopicRationals and Radicals DefinitionAn irrational number is a number that cannot be expressed as a ratio of two integers. Its decimal form is non-repeating and non-terminating. |
Rational Expressions |

|
Definition--Rationals and Radicals--Irrational Number 2 | Irrational Number 2TopicRationals and Radicals DefinitionAn irrational number is a number that cannot be expressed as a ratio of two integers. Its decimal form is non-repeating and non-terminating. |
Rational Expressions |

|
Definition--Rationals and Radicals--Laws of Rational Exponents | Laws of Rational ExponentsTopicRationals and Radicals DefinitionThe laws of rational exponents describe how to handle exponents that are fractions, including rules for multiplication, division, and raising a power to a power. DescriptionThe Laws of Rational Exponents are vital in the study of Rational Numbers, Expressions, Equations, and Functions. These laws provide a framework for simplifying expressions involving exponents that are fractions. For example, the law am/n=n√am |
Rational Expressions |

|
Definition--Rationals and Radicals--nth Root | nth RootTopicRationals and Radicals DefinitionThe nth root of a number is a value that, when raised to the power of n, gives the original number. It is denoted as n√a DescriptionThe nth Root is a fundamental concept in the study of Radical Numbers, Expressions, Equations, and Functions. It generalizes the idea of square roots and cube roots to any positive integer n. For example, the cube root of 8 is 2 because 23=8 |
Radical Expressions |
|
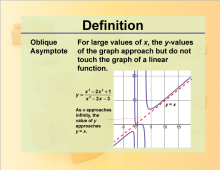
Definition--Rationals and Radicals--Oblique Asymptote | Oblique AsymptoteTopicRationals and Radicals DefinitionAn oblique asymptote is a diagonal line that the graph of a function approaches as the input values become very large or very small. DescriptionOblique Asymptotes are important in the study of Rational Numbers, Expressions, Equations, and Functions. They occur in rational functions where the degree of the numerator is one more than the degree of the denominator. For example, the function f(x)=x2+1x |
Rational Functions and Equations |

|
Definition--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression | Partial Fraction Decomposition of a Rational ExpressionTopicRationals and Radicals DefinitionPartial fraction decomposition is a method used to express a rational expression as a sum of simpler fractions. DescriptionPartial Fraction Decomposition is a powerful tool in the study of Rational Numbers, Expressions, Equations, and Functions. It involves breaking down a complex rational expression into a sum of simpler fractions, which are easier to integrate or differentiate. For example, the rational function 2x+3(x+1)(x−2) can be decomposed into |
Rational Expressions |

|
Definition--Rationals and Radicals--Radical Equations | Radical EquationsTopicRationals and Radicals DefinitionRadical equations are equations in which the variable is inside a radical, such as a square root or cube root. DescriptionRadical Equations are a fundamental aspect of Radical Numbers, Expressions, Equations, and Functions. These equations involve variables within radical signs, such as square roots or cube roots. Solving radical equations typically requires isolating the radical on one side of the equation and then squaring both sides to eliminate the radical. For example, to solve √x+3=5 one would square both sides to obtain x+3=25 |
Radical Functions and Equations |

|
Definition--Rationals and Radicals--Radical Expression | Radical ExpressionTopicRationals and Radicals DefinitionA radical expression is an expression that contains a radical symbol, which indicates the root of a number. DescriptionRadical Expressions are a core component of Radical Numbers, Expressions, Equations, and Functions. These expressions involve roots, such as square roots, cube roots, or higher-order roots, and are denoted by the radical symbol (√). For example, the expression √16 |
Radical Expressions |