
Illustrative Math Alignment: Grade 7 Unit 5
Rational Number Arithmetic
Lesson 7: Adding and Subtracting to Solve Problems
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topics |
|---|---|---|---|

|
Quizlet Flash Cards: Subtracting Rational Numbers, Set 07 | Subtract rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3gT8TIq |
Subtract Multiple-Digit Numbers |

|
Quizlet Flash Cards: Subtracting Rational Numbers, Set 08 | Subtract rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3gT8TIq |
Subtract Multiple-Digit Numbers |

|
Quizlet Flash Cards: Subtracting Rational Numbers, Set 09 | Subtract rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3gT8TIq |
Subtract Multiple-Digit Numbers |

|
Quizlet Flash Cards: Subtracting Rational Numbers, Set 10 | Subtract rational numbers in this 20-flash card set. The values of the numerators and denominators are in the range -10 to 10. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/3gT8TIq |
Subtract Multiple-Digit Numbers |

|
Video Definition 1--Rationals and Radicals--Addition of Rational Expressions | Video Definition 1--Rationals and Radicals--Addition of Rational Expressions
TopicRationals and Radicals DescriptionAddition of rational expressions involves combining rational expressions to create a new rational expression, often requiring a common denominator. Examples include 1 / x + 1 / 2x = 3 / 2x and 1 / (x + 1) + 1 / (x - 1) = 2x / (x2 - 1). This term introduces the concept of combining rational expressions, which is fundamental to operations involving fractions with polynomial expressions. |
Rational Functions and Equations |

|
Video Definition 1--Rationals and Radicals--Addition of Rational Expressions (Spanish Audio) | Video Definition 1--Rationals and Radicals--Addition of Rational Expressions (Spanish Audio)
TopicRationals and Radicals |
Rational Functions and Equations |

|
Video Definition 10--Rationals and Radicals--Geometric Mean | Video Definition 10--Rationals and Radicals--Geometric Mean
TopicRationals and Radicals DescriptionThe geometric mean is the nth root of the product of n terms. Examples include the geometric mean of 3 and 12, √(3 × 12) = 6, and the geometric mean of 3, 4, and 12, ∛(3 × 4 × 12) ≈ 5.24. Geometric mean connects multiplication and roots, commonly used in statistics, geometry, and proportional reasoning. |
Radical Expressions |

|
Video Definition 10--Rationals and Radicals--Geometric Mean (Spanish Audio) | Video Definition 10--Rationals and Radicals--Geometric Mean (Spanish Audio)
TopicRationals and Radicals DescriptionThe geometric mean is the nth root of the product of n terms. Examples include the geometric mean of 3 and 12, √(3 × 12) = 6, and the geometric mean of 3, 4, and 12, ∛(3 × 4 × 12) ≈ 5.24. Geometric mean connects multiplication and roots, commonly used in statistics, geometry, and proportional reasoning. This video includes Spanish audio and can be used with multilingual learners. |
Radical Expressions |
|
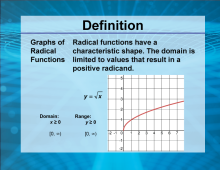
Video Definition 11--Rationals and Radicals--Graphs of Radical Functions | Video Definition 11--Rationals and Radicals--Graphs of Radical Functions
TopicRationals and Radicals DescriptionGraphs of radical functions have a characteristic shape where the domain is limited to values resulting in a positive radicand. For y = √x, the domain is x >= 0, and the range is y >= 0. This highlights the inherent properties of square root functions. Introduces the concept of radical graphs and their domain/range constraints, setting a foundation for graph behavior analysis. |
Radical Functions and Equations |

|
Video Definition 11--Rationals and Radicals--Graphs of Radical Functions (Spanish Audio) | Video Definition 11--Rationals and Radicals--Graphs of Radical Functions (Spanish Audio)
TopicRationals and Radicals |
Radical Functions and Equations |
|
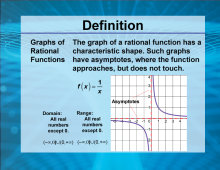
Video Definition 12--Rationals and Radicals--Graphs of Rational Functions | Video Definition 12--Rationals and Radicals--Graphs of Rational Functions
TopicRationals and Radicals DescriptionGraphs of rational functions often feature asymptotes, which are lines the graph approaches but never touches. For example, f(x) = 1 / x has vertical and horizontal asymptotes at x = 0 and y = 0, respectively. The domain and range exclude zero. Explains the unique characteristics of rational function graphs and the significance of asymptotes in defining their behavior. |
Rational Functions and Equations |

|
Video Definition 12--Rationals and Radicals--Graphs of Rational Functions (Spanish Audio) | Video Definition 12--Rationals and Radicals--Graphs of Rational Functions (Spanish Audio)
TopicRationals and Radicals DescriptionGraphs of rational functions often feature asymptotes, which are lines the graph approaches but never touches. For example, f(x) = 1 / x has vertical and horizontal asymptotes at x = 0 and y = 0, respectively. The domain and range exclude zero. Explains the unique characteristics of rational function graphs and the significance of asymptotes in defining their behavior. |
Rational Functions and Equations |
|
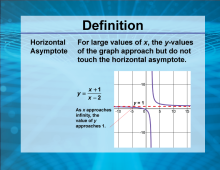
Video Definition 13--Rationals and Radicals--Horizontal Asymptote | Video Definition 13--Rationals and Radicals--Horizontal Asymptote
TopicRationals and Radicals DescriptionHorizontal asymptotes describe the behavior of a graph as x approaches infinity or negative infinity. For example, the equation y = (x + 1) / (x - 2) has a horizontal asymptote at y = 1, demonstrating long-term behavior of the function. Focuses on the role of horizontal asymptotes in describing the long-term trends of rational functions. |
Rational Functions and Equations |

|
Video Definition 13--Rationals and Radicals--Horizontal Asymptote (Spanish Audio) | Video Definition 13--Rationals and Radicals--Horizontal Asymptote (Spanish Audio)
TopicRationals and Radicals DescriptionHorizontal asymptotes describe the behavior of a graph as x approaches infinity or negative infinity. For example, the equation y = (x + 1) / (x - 2) has a horizontal asymptote at y = 1, demonstrating long-term behavior of the function. Focuses on the role of horizontal asymptotes in describing the long-term trends of rational functions. |
Rational Functions and Equations |

|
Video Definition 14--Rationals and Radicals--Index | Video Definition 14--Rationals and Radicals--Index
TopicRationals and Radicals DescriptionThe index of a radical specifies the root being taken, such as the square root (index 2) or cube root (index 3). Examples include √25 for index 2 and the cube root of 27 for index 3. Defines and applies the concept of indices in radicals, foundational for understanding roots and powers. |
Radical Expressions |

|
Video Definition 14--Rationals and Radicals--Index (Spanish Audio) | Video Definition 14--Rationals and Radicals--Index (Spanish Audio)
TopicRationals and Radicals DescriptionThe index of a radical specifies the root being taken, such as the square root (index 2) or cube root (index 3). Examples include √25 for index 2 and the 3√27 for index 3. Defines and applies the concept of indices in radicals, foundational for understanding roots and powers. This video includes Spanish audio and can be used with multilingual learners. |
Radical Expressions |

|
Video Definition 15--Rationals and Radicals--Integer | Video Definition 15--Rationals and Radicals--Integer
TopicRationals and Radicals DescriptionIntegers are a subset of rational numbers including positive, negative, and zero values, represented by {..., -3, -2, -1, 0, 1, 2, 3, ...}. This emphasizes their role in forming the basis of discrete mathematics. Introduces integers as a key component of number systems, aiding comprehension of rational numbers. |
Rational Functions and Equations |

|
Video Definition 15--Rationals and Radicals--Integer (Spanish Audio) | Video Definition 15--Rationals and Radicals--Integer (Spanish Audio)
TopicRationals and Radicals DescriptionIntegers are a subset of rational numbers including positive, negative, and zero values, represented by {..., -3, -2, -1, 0, 1, 2, 3, ...}. This emphasizes their role in forming the basis of discrete mathematics. Introduces integers as a key component of number systems, aiding comprehension of rational numbers. This video includes Spanish audio and can be used with multilingual learners. |
Rational Functions and Equations |
|
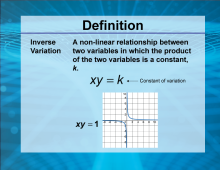
Video Definition 16--Rationals and Radicals--Inverse Variation | Video Definition 16--Rationals and Radicals--Inverse Variation
TopicRationals and Radicals DescriptionInverse variation describes a non-linear relationship where the product of two variables is a constant k. For instance, xy = k is graphically represented by a hyperbola, illustrating how one variable inversely depends on the other. Describes inverse variation as a key relationship in algebra, foundational for understanding non-linear equations. |
Rational Functions and Equations |

|
Video Definition 16--Rationals and Radicals--Inverse Variation (Spanish Audio) | Video Definition 16--Rationals and Radicals--Inverse Variation (Spanish Audio)
TopicRationals and Radicals DescriptionInverse variation describes a non-linear relationship where the product of two variables is a constant k. For instance, xy = k is graphically represented by a hyperbola, illustrating how one variable inversely depends on the other. Describes inverse variation as a key relationship in algebra, foundational for understanding non-linear equations. |
Rational Functions and Equations |

|
Video Definition 17--Rationals and Radicals--Irrational Number | Video Definition 17--Rationals and Radicals--Irrational Number
TopicRationals and Radicals DescriptionIrrational numbers cannot be expressed as ratios of integers. Examples include pi and √2, demonstrating their importance in representing real-world measurements and non-terminating decimals. Highlights the significance of irrational numbers in advanced mathematics and real-world applications. |
Rational Expressions |

|
Video Definition 17--Rationals and Radicals--Irrational Number (Spanish Audio) | Video Definition 17--Rationals and Radicals--Irrational Number (Spanish Audio)
TopicRationals and Radicals DescriptionIrrational numbers cannot be expressed as ratios of integers. Examples include pi and √2, demonstrating their importance in representing real-world measurements and non-terminating decimals. Highlights the significance of irrational numbers in advanced mathematics and real-world applications. This video includes Spanish audio and can be used with multilingual learners. |
Rational Expressions |

|
Video Definition 18--Rationals and Radicals--Irrational Number 2 | Video Definition 18--Rationals and Radicals--Irrational Number 2
TopicRationals and Radicals DescriptionAnother definition of irrational numbers emphasizes their non-representability as fractions. Examples include e and √3, reinforcing their role in mathematical constants and transcendental equations. Reinforces the understanding of irrational numbers by presenting additional examples and contexts. |
Rational Expressions |

|
Video Definition 18--Rationals and Radicals--Irrational Number 2 (Spanish Audio) | Video Definition 18--Rationals and Radicals--Irrational Number 2 (Spanish Audio)
TopicRationals and Radicals DescriptionAnother definition of irrational numbers emphasizes their non-representability as fractions. Examples include e and √3, reinforcing their role in mathematical constants and transcendental equations. Reinforces the understanding of irrational numbers by presenting additional examples and contexts. This video includes Spanish audio and can be used with multilingual learners. |
Rational Expressions |

|
Video Definition 19--Rationals and Radicals--Laws of Rational Exponents | Video Definition 19--Rationals and Radicals--Laws of Rational Exponents
TopicRationals and Radicals DescriptionThe laws of rational exponents extend the rules of exponents to fractional powers. For instance, 2(1/2) * 2(1/2) = 2(1/2 + 1/2) = 2, demonstrating the connection between exponents and roots. Explains the fundamental laws governing rational exponents, linking them to both roots and powers. |
Rational Expressions |

|
Video Definition 19--Rationals and Radicals--Laws of Rational Exponents (Spanish Audio) | Video Definition 19--Rationals and Radicals--Laws of Rational Exponents (Spanish Audio)
TopicRationals and Radicals DescriptionThe laws of rational exponents extend the rules of exponents to fractional powers. For instance, 2(1/2) * 2(1/2) = 2(1/2 + 1/2) = 2, demonstrating the connection between exponents and roots. Explains the fundamental laws governing rational exponents, linking them to both roots and powers. |
Rational Expressions |
|
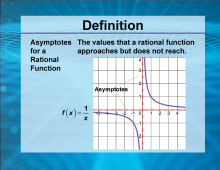
Video Definition 2--Rationals and Radicals--Asymptotes for a Rational Function | Video Definition 2--Rationals and Radicals--Asymptotes for a Rational Function
TopicRationals and Radicals DescriptionAsymptotes for a rational function are the values a function approaches but does not reach. An example is the function f(x) = 1 / x, where the graph has vertical and horizontal asymptotes at x = 0 and y = 0, respectively. This concept explains the behavior of rational functions at extreme values, helping understand their graphs and limits. |
Rational Functions and Equations |

|
Video Definition 2--Rationals and Radicals--Asymptotes for a Rational Function (Spanish Audio) | Video Definition 2--Rationals and Radicals--Asymptotes for a Rational Function (Spanish Audio)
TopicRationals and Radicals DescriptionAsymptotes for a rational function are the values a function approaches but does not reach. An example is the function f(x) = 1 / x, where the graph has vertical and horizontal asymptotes at x = 0 and y = 0, respectively. This concept explains the behavior of rational functions at extreme values, helping understand their graphs and limits. |
Rational Functions and Equations |

|
Video Definition 20--Rationals and Radicals--Multiplication of Rational Expressions | Video Definition 20--Rationals and Radicals--Multiplication of Rational Expressions
TopicRationals and Radicals DescriptionMultiplication of rational expressions involves multiplying the numerators and denominators of each expression. For example, (x / (x + 1)) * ((x - 1) / 3) simplifies to (x * (x - 1)) / (3 * (x + 1)), illustrating its application in simplifying complex expressions. Covers the multiplication of rational expressions, essential for algebraic simplifications and solving equations. |
Rational Functions and Equations |

|
Video Definition 20--Rationals and Radicals--Multiplication of Rational Expressions (Spanish Audio) | Video Definition 20--Rationals and Radicals--Multiplication of Rational Expressions (Spanish Audio)
TopicRationals and Radicals |
Rational Functions and Equations |

|
Video Definition 21--Rationals and Radicals--nth Root | Video Definition 21--Rationals and Radicals--nth Root
TopicRationals and Radicals |
Radical Expressions |

|
Video Definition 21--Rationals and Radicals--nth Root (Spanish Audio) | Video Definition 21--Rationals and Radicals--nth Root (Spanish Audio)
TopicRationals and Radicals |
Radical Expressions |
|
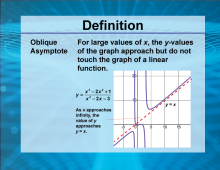
Video Definition 22--Rationals and Radicals--Oblique Asymptote | Video Definition 22--Rationals and Radicals--Oblique Asymptote
TopicRationals and Radicals DescriptionAn oblique asymptote occurs when, for large values of x, the y-values of the graph approach but do not touch the graph of a linear function. An example is given where y = (x3 - 2x2 + 1) / (x2 - 2x - 3) approaches y = x as x approaches infinity. This term provides insight into the behavior of rational functions, essential for graphing and understanding limits in radical and rational contexts. |
Rational Functions and Equations |

|
Video Definition 22--Rationals and Radicals--Oblique Asymptote (Spanish Audio) | Video Definition 22--Rationals and Radicals--Oblique Asymptote (Spanish Audio)
TopicRationals and Radicals |
Rational Functions and Equations |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio) | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio)
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 24--Rationals and Radicals--Perfect Cube | Video Definition 24--Rationals and Radicals--Perfect Cube
TopicRationals and Radicals DescriptionA perfect cube is a number or polynomial that is the cube of an integer or linear expression. Examples include 125 = 53 and the polynomial (x + 1)3 = x3 + 3x2 + 3x + 1. Understanding perfect cubes is essential for simplifying expressions and solving radical equations involving cube roots. |
Radical Expressions |

|
Video Definition 24--Rationals and Radicals--Perfect Cube (Spanish Audio) | Video Definition 24--Rationals and Radicals--Perfect Cube (Spanish Audio)
TopicRationals and Radicals DescriptionA perfect cube is a number or polynomial that is the cube of an integer or linear expression. Examples include 125 = 53 and the polynomial (x + 1)3 = x3 + 3x2 + 3x + 1. Understanding perfect cubes is essential for simplifying expressions and solving radical equations involving cube roots. This video includes Spanish audio and can be used with multilingual learners. |
Radical Expressions |

|
Video Definition 25--Rationals and Radicals--Perfect Square | Video Definition 25--Rationals and Radicals--Perfect Square
TopicRationals and Radicals DescriptionA perfect square is a number or polynomial that is the square of an integer or linear expression. Examples include 64 = 82 and the polynomial (x - 1)2 = x2 - 2x + 1. Perfect squares are foundational in factoring, completing the square, and simplifying radical expressions. |
Radical Expressions |

|
Video Definition 25--Rationals and Radicals--Perfect Square (Spanish Audio) | Video Definition 25--Rationals and Radicals--Perfect Square (Spanish Audio)
TopicRationals and Radicals DescriptionA perfect square is a number or polynomial that is the square of an integer or linear expression. Examples include 64 = 82 and the polynomial (x - 1)2 = x2 - 2x + 1. Perfect squares are foundational in factoring, completing the square, and simplifying radical expressions. This video includes Spanish audio and can be used with multilingual learners. |
Radical Expressions |

|
Video Definition 26--Rationals and Radicals--Principal Square Root | Video Definition 26--Rationals and Radicals--Principal Square Root
TopicRationals and Radicals DescriptionThe principal square root is the non-negative square root of a non-negative real number. Examples include √36 = 6 and √81 = 9, excluding their negative counterparts. Clarifies the distinction between principal and negative roots, which is fundamental when solving radical equations. |
Radical Expressions |

|
Video Definition 26--Rationals and Radicals--Principal Square Root (Spanish Audio) | Video Definition 26--Rationals and Radicals--Principal Square Root (Spanish Audio)
TopicRationals and Radicals DescriptionThe principal square root is the non-negative square root of a non-negative real number. Examples include √36 = 6 and √81 = 9, excluding their negative counterparts. Clarifies the distinction between principal and negative roots, which is fundamental when solving radical equations. This video includes Spanish audio and can be used with multilingual learners. |
Radical Expressions |

|
Video Definition 27--Rationals and Radicals--Radical Equations | Video Definition 27--Rationals and Radicals--Radical Equations
TopicRationals and Radicals DescriptionRadical equations involve solving expressions with radicals by raising both sides to a power. An example solves √(x + 2) = x, resulting in x = 2 or x = -1. This term demonstrates how radicals can be manipulated algebraically to find solutions, integrating concepts of nth roots and square roots. |
Radical Functions and Equations |

|
Video Definition 27--Rationals and Radicals--Radical Equations (Spanish Audio) | Video Definition 27--Rationals and Radicals--Radical Equations (Spanish Audio)
TopicRationals and Radicals DescriptionRadical equations involve solving expressions with radicals by raising both sides to a power. An example solves √(x + 2) = x, resulting in x = 2 or x = -1. This term demonstrates how radicals can be manipulated algebraically to find solutions, integrating concepts of nth roots and square roots. This video includes Spanish audio and can be used with multilingual learners. |
Radical Functions and Equations |

|
Video Definition 28--Rationals and Radicals--Radical Expression | Video Definition 28--Rationals and Radicals--Radical Expression
TopicRationals and Radicals DescriptionA radical expression includes terms under a radical sign, such as √2 or x + √(b2 - a). Examples illustrate simple and complex radical forms. Defines and illustrates the structure of radical expressions, serving as a basis for simplification and operations. |
Radical Expressions |

|
Video Definition 28--Rationals and Radicals--Radical Expression (Spanish Audio) | Video Definition 28--Rationals and Radicals--Radical Expression (Spanish Audio)
TopicRationals and Radicals DescriptionA radical expression includes terms under a radical sign, such as √2 or x + √(b2 - a). Examples illustrate simple and complex radical forms. Defines and illustrates the structure of radical expressions, serving as a basis for simplification and operations. This video includes Spanish audio and can be used with multilingual learners. |
Radical Expressions |

|
Video Definition 29--Rationals and Radicals--Radical Function | Video Definition 29--Rationals and Radicals--Radical Function
TopicRationals and Radicals DescriptionA radical function includes an independent variable under the radical sign, such as y = √x or y = 4√(x - 2) + 3. Examples showcase square root, cube root, and higher-order radical functions. Connects radicals with functions, demonstrating their graphical representation and behavior. |
Radical Expressions |

|
Video Definition 29--Rationals and Radicals--Radical Function (Spanish Audio) | Video Definition 29--Rationals and Radicals--Radical Function (Spanish Audio)
TopicRationals and Radicals DescriptionA radical function includes an independent variable under the radical sign, such as y = √x or y = 4√(x - 2) + 3. Examples showcase square root, cube root, and higher-order radical functions. Connects radicals with functions, demonstrating their graphical representation and behavior. This video includes Spanish audio and can be used with multilingual learners. |
Radical Expressions |

|
Video Definition 3--Rationals and Radicals--Complex Number | Video Definition 3--Rationals and Radicals--Complex Number
TopicRationals and Radicals DescriptionA complex number is a non-real number expressed in forms such as a + bi, r e(iθ), or r cos(θ) + i r sin(θ). Examples include 2 + 5i, 12 e(iπ/4), and 5 cos(60°) + i 5 sin(60°). Complex numbers extend the number system to include imaginary units, enabling solutions to equations like x2 = -1. |
Radical Expressions |

|
Video Definition 3--Rationals and Radicals--Complex Number (Spanish Audio) | Video Definition 3--Rationals and Radicals--Complex Number (Spanish Audio)
TopicRationals and Radicals DescriptionA complex number is a non-real number expressed in forms such as a + bi, r e(iθ), or r cos(θ) + i r sin(θ). Examples include 2 + 5i, 12 e(iπ/4), and 5 cos(60°) + i 5 sin(60°). Complex numbers extend the number system to include imaginary units, enabling solutions to equations like x2 = -1. This video includes Spanish audio and can be used with multilingual learners. |
Radical Expressions |