Illustrative Math Alignment: Grade 7 Unit 7
Angles, Triangles, and Prisms
Lesson 1: Relationships of Angles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|
|
Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles with Common Base--Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Labeled | Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Labeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Unlabeled | Math Clip Art--Triangles--Two Triangles with Common Base--Non Congruent--Unlabeled
This is from a collection of triangular shapes. They come labeled and unlabeled. |
Applications of Triangles |
|
Math Clip Art: Comparing Right Triangles | Math Clip Art: Comparing Right Triangles Use these clip art images and the background grid to test if the right triangles are similar. |
Right Triangles |
|
Math Clip Art: Right Triangles on a Grid Background | Math Clip Art: Right Triangles on a Grid Background Have students explore right triangles on a grid background. |
Right Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 1 | Math Example--Area and Perimeter--Triangles: Example 1TopicGeometry DescriptionThis example demonstrates how to calculate the area of a scalene triangle. The triangle has sides measuring 5, 7, and 9 units, with a height of 3 units from the base of 7. To find the area, we use the formula A = 1/2 * b * h. In this case, A = 1/2 * 7 * 3 = 10.5 square units. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 10 | Math Example--Area and Perimeter--Triangles: Example 10TopicGeometry DescriptionThis example explores the area calculation of an equilateral triangle using algebraic expressions. The triangle has all sides labeled as x, with the height expressed as (√3/2) * x. Students are guided through the process of deriving and applying the area formula for this general case of an equilateral triangle. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 11 | Math Example--Area and Perimeter--Triangles: Example 11TopicGeometry DescriptionThis example demonstrates the calculation of area for a right triangle with specific dimensions. The triangle has legs measuring 8 and 15 units. Students are guided through the process of applying the area formula to this straightforward case. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 12 | Math Example--Area and Perimeter--Triangles: Example 12TopicGeometry DescriptionThis example introduces algebraic expressions in the context of right triangle area calculations. The triangle's legs are labeled x and y, challenging students to express the area formula using these variables. Integrating algebra into geometric problems is a key skill in advanced mathematics. This collection of examples helps teach this topic by demonstrating how algebraic expressions can represent right triangle dimensions. Students learn to manipulate these expressions within the area formula, deepening their understanding of both algebra and geometry. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 13 | Math Example--Area and Perimeter--Triangles: Example 13TopicGeometry DescriptionThis example focuses on calculating the area of an isosceles right triangle. The triangle has two equal legs measuring 13 units each, with angles of 45 degrees. Students are guided through applying the area formula to this specific case, which combines properties of both isosceles and right triangles. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 14 | Math Example--Area and Perimeter--Triangles: Example 14TopicGeometry DescriptionThis example combines the concepts of isosceles right triangles and algebraic expressions. The triangle has two equal legs labeled as x, with angles of 45 degrees. Students are challenged to express the area formula using this variable, applying their knowledge of both triangle properties and algebraic manipulation. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 15 | Math Example--Area and Perimeter--Triangles: Example 15TopicGeometry DescriptionThis example focuses on calculating the area of a 30-60-90 right triangle. The triangle has a base of 16 units and a height of 8√3 units. Students are guided through applying the area formula to this specific case, which involves working with irrational numbers. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 16 | Math Example--Area and Perimeter--Triangles: Example 16TopicGeometry DescriptionThis example combines the properties of 30-60-90 right triangles with algebraic expressions. The triangle has a base of x + 5 and a height of (x + 5)/2 * √3. Students are challenged to express the area formula using these algebraic terms, applying their knowledge of both special right triangles and algebraic manipulation. |
Area and Perimeter of Triangles |
|
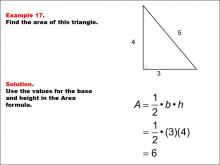
Math Example--Area and Perimeter--Triangles: Example 17 | Math Example--Area and Perimeter--Triangles: Example 17TopicGeometry DescriptionThis example focuses on calculating the area of a 3-4-5 right triangle. This triangle is a special case of right triangles with integer side lengths. Students are guided through applying the area formula to this specific case, which is straightforward due to its simple dimensions. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 18 | Math Example--Area and Perimeter--Triangles: Example 18TopicGeometry DescriptionThis example combines the concept of a 3-4-5 right triangle with algebraic expressions. The triangle's sides are labeled as 3(x + 4), 4(x + 4), and 5(x + 4). Students are challenged to express the area formula using these algebraic terms, applying their knowledge of both special right triangles and algebraic manipulation. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 19 | Math Example--Area and Perimeter--Triangles: Example 19TopicGeometry DescriptionThis example focuses on calculating the area of a right triangle with sides 5, 12, and 13 units. Students are guided through applying the area formula to this specific case, which involves a right triangle with integer side lengths that satisfy the Pythagorean theorem. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 2 | Math Example--Area and Perimeter--Triangles: Example 2TopicGeometry DescriptionThis example illustrates the calculation of a scalene triangle's area using algebraic expressions. The triangle has sides labeled x, y, z, with a height labeled w from the base x. To find the area, we use the formula A = 1/2 * b * h. In this case, A = 1/2 * x * w = xw / 2. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 20 | Math Example--Area and Perimeter--Triangles: Example 20TopicGeometry DescriptionThis example combines the concept of a 5-12-13 right triangle with algebraic expressions. The triangle's sides are labeled as 5(x - 7), 12(x - 7), and 13(x - 7). Students are challenged to express the area formula using these algebraic terms, applying their knowledge of both special right triangles and algebraic manipulation. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 21 | Math Example--Area and Perimeter--Triangles: Example 21TopicGeometry DescriptionThis example introduces the concept of perimeter calculation for a scalene triangle. The triangle has sides measuring 5, 7, and 9 units. Students are guided through the process of calculating the perimeter by simply adding the lengths of all sides. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 22 | Math Example--Area and Perimeter--Triangles: Example 22TopicGeometry DescriptionThis example introduces the concept of perimeter calculation for a scalene triangle using algebraic expressions. The triangle has sides labeled x, y, and z. Students are guided through the process of expressing the perimeter using these variables. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 23 | Math Example--Area and Perimeter--Triangles: Example 23TopicGeometry DescriptionThis example focuses on calculating the perimeter of an acute triangle with specific side lengths. The triangle has sides measuring 10, 11, and 12 units, with angles of 50 and 60 degrees. Students are guided through the process of adding these side lengths to find the perimeter. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 24 | Math Example--Area and Perimeter--Triangles: Example 24TopicGeometry DescriptionThis example combines the concept of perimeter calculation for an acute triangle with algebraic expressions. The triangle has sides labeled as x - 3, x - 4, and x. Students are challenged to express the perimeter formula using these algebraic terms, applying their knowledge of both geometry and algebraic manipulation. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 25 | Math Example--Area and Perimeter--Triangles: Example 25TopicGeometry DescriptionThis example focuses on calculating the perimeter of an obtuse triangle with specific side lengths. The triangle has sides measuring 15, 6, and 18 units, with an obtuse angle of 120 degrees. Students are guided through the process of adding these side lengths to find the perimeter. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 26 | Math Example--Area and Perimeter--Triangles: Example 26TopicGeometry DescriptionThis example combines the concept of perimeter calculation for an obtuse triangle with algebraic expressions. The triangle has sides labeled as x + 1, x + 2, and x + 4, with an obtuse angle of 120 degrees. Students are challenged to express the perimeter formula using these algebraic terms, applying their knowledge of both geometry and algebraic manipulation. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 27 | Math Example--Area and Perimeter--Triangles: Example 27TopicGeometry DescriptionThis example focuses on calculating the perimeter of an isosceles triangle with specific side lengths. The triangle has two equal sides measuring 10 units and a base of 8 units. Students are guided through the process of adding these side lengths to find the perimeter. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 28 | Math Example--Area and Perimeter--Triangles: Example 28TopicGeometry DescriptionThis example combines the concept of perimeter calculation for an isosceles triangle with algebraic expressions. The triangle has two equal sides labeled as x + 4 and a base of x - 3. Students are challenged to express the perimeter formula using these algebraic terms, applying their knowledge of both geometry and algebraic manipulation. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 29 | Math Example--Area and Perimeter--Triangles: Example 29TopicGeometry DescriptionThis example focuses on calculating the perimeter of an equilateral triangle with specific side lengths. The triangle has all sides measuring 15 units. Students are guided through the process of adding these side lengths to find the perimeter, emphasizing the simplicity of calculations for equilateral triangles. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 3 | Math Example--Area and Perimeter--Triangles: Example 3TopicGeometry DescriptionThis example demonstrates how to calculate the area of an acute triangle. The triangle has angles labeled as 50° and 60°, with a base measuring 12 units and a height of 8 units. To find the area, we use the formula A = 1/2 * b * h. In this case, A = 1/2 * 12 * 8 = 48 square units. Understanding the area of triangles is a fundamental concept in geometry that applies to various real-world situations. This collection of examples helps students visualize different types of triangles and compute their areas accurately using given dimensions. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 30 | Math Example--Area and Perimeter--Triangles: Example 30TopicGeometry DescriptionThis example combines the concept of perimeter calculation for an equilateral triangle with algebraic expressions. The triangle has all sides labeled as 2x + 3. Students are challenged to express the perimeter formula using this algebraic term, applying their knowledge of both geometry and algebraic manipulation. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 31 | Math Example--Area and Perimeter--Triangles: Example 31TopicGeometry DescriptionThis example demonstrates the process of finding the perimeter of a right triangle when only two sides are given. The triangle has sides measuring 7 and 12 units. Students are guided through using the Pythagorean Theorem to find the length of the hypotenuse before calculating the perimeter. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 32 | Math Example--Area and Perimeter--Triangles: Example 32TopicGeometry DescriptionThis example demonstrates the process of finding the perimeter of a right triangle with algebraic expressions for its sides. The triangle has legs labeled as x - 2 and 2x. Students are guided through using the Pythagorean Theorem to find the hypotenuse and then calculating the perimeter using algebraic manipulation. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 33 | Math Example--Area and Perimeter--Triangles: Example 33TopicGeometry DescriptionThis example focuses on calculating the perimeter of an isosceles right triangle. The triangle has two equal sides of length 12 units and angles of 45 degrees. Students are guided through the process of using the Pythagorean Theorem to find the hypotenuse and then calculating the perimeter. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 34 | Math Example--Area and Perimeter--Triangles: Example 34TopicGeometry DescriptionThis example combines the concept of isosceles right triangles with algebraic expressions. The triangle has two equal sides labeled as x + 2 and angles of 45 degrees. Students are challenged to use the Pythagorean Theorem to find the hypotenuse and then express the perimeter using algebraic terms. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 35 | Math Example--Area and Perimeter--Triangles: Example 35TopicGeometry DescriptionThis example focuses on calculating the perimeter of a 30-60-90 right triangle. The triangle has sides of 12 and 24 units, with angles of 30 and 60 degrees. Students are guided through the process of using the Pythagorean Theorem to find the third side and then calculating the perimeter. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 36 | Math Example--Area and Perimeter--Triangles: Example 36TopicGeometry DescriptionThis example combines the concept of 30-60-90 right triangles with algebraic expressions. The triangle has sides labeled as x - 10 and 2(x - 10), with angles of 30 and 60 degrees. Students are challenged to use the Pythagorean Theorem to find the third side and then express the perimeter using algebraic terms. |
Area and Perimeter of Triangles |
|
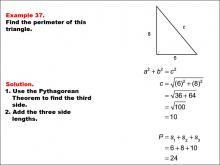
Math Example--Area and Perimeter--Triangles: Example 37 | Math Example--Area and Perimeter--Triangles: Example 37TopicGeometry DescriptionThis example demonstrates the process of finding the perimeter of a right triangle with sides of 6 and 8 units. Students are guided through using the Pythagorean Theorem to find the hypotenuse and then calculating the perimeter by adding all three sides. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 38 | Math Example--Area and Perimeter--Triangles: Example 38TopicGeometry DescriptionThis example combines the concept of right triangle perimeter with algebraic expressions. The triangle has sides labeled as 3(x + 4) and 4(x + 4). Students are challenged to use the Pythagorean Theorem to find the hypotenuse and then express the perimeter using algebraic terms. |
Area and Perimeter of Triangles |
|
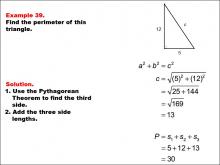
Math Example--Area and Perimeter--Triangles: Example 39 | Math Example--Area and Perimeter--Triangles: Example 39TopicGeometry DescriptionThis example demonstrates the process of finding the perimeter of a right triangle with sides of 5 and 12 units. Students are guided through using the Pythagorean Theorem to find the hypotenuse and then calculating the perimeter by adding all three sides. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 4 | Math Example--Area and Perimeter--Triangles: Example 4TopicGeometry DescriptionThis example introduces students to calculating the area of an acute triangle using algebraic expressions. The triangle has angles of 50 and 60 degrees, with the base labeled as x and the height as x - 4. Students are tasked with expressing the area formula using these variables. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 40 | Math Example--Area and Perimeter--Triangles: Example 40TopicGeometry DescriptionThis example combines the concept of right triangle perimeter with complex algebraic expressions. The triangle has sides labeled as 5(x + 10) and 12(x + 10). Students are challenged to use the Pythagorean Theorem to find the hypotenuse and then express the perimeter using algebraic terms. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 5 | Math Example--Area and Perimeter--Triangles: Example 5TopicGeometry DescriptionThis example demonstrates the calculation of area for an obtuse triangle. The triangle has a base of 15 units, a height of 8 units, and includes a 120-degree angle. Students are guided through the process of applying the area formula for this specific case. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 6 | Math Example--Area and Perimeter--Triangles: Example 6TopicGeometry DescriptionThis example combines the concepts of obtuse triangles and algebraic expressions. The triangle has a base of x + 1 and a height of x - 1, with a 120-degree angle. Students are challenged to express the area formula using these algebraic terms. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 7 | Math Example--Area and Perimeter--Triangles: Example 7TopicGeometry DescriptionThis example focuses on calculating the area of an isosceles triangle. The triangle has two equal angles of 65° and a base angle of 50°. The base is 8 units long, and the height is 10 units. Students are guided through applying the standard area formula to this specific case. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 8 | Math Example--Area and Perimeter--Triangles: Example 8TopicGeometry DescriptionThis example combines isosceles triangles with algebraic expressions. The triangle has two equal angles of 65° and a base angle of 50°. The base is expressed as x - 3, and the height as x + 3. Students are challenged to formulate the area using these algebraic terms. |
Area and Perimeter of Triangles |
|
Math Example--Area and Perimeter--Triangles: Example 9 | Math Example--Area and Perimeter--Triangles: Example 9TopicGeometry DescriptionThis example focuses on calculating the area of an equilateral triangle. The triangle has all angles equal to 60°, a base of 12 units, and a height of 6√3 units. Students are guided through applying the area formula using these specific dimensions, which involve a square root. |
Area and Perimeter of Triangles |
|
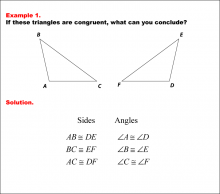
Math Example--Geometric Shapes--Congruent Triangles--Example 1 | Math Example--Geometric Shapes--Congruent Triangles--Example 1
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Triangle |
|
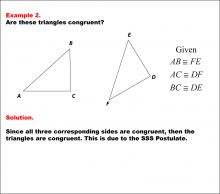
Math Example--Geometric Shapes--Congruent Triangles--Example 2 | Math Example--Geometric Shapes--Congruent Triangles--Example 2
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Triangle |
|
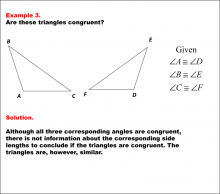
Math Example--Geometric Shapes--Congruent Triangles--Example 3 | Math Example--Geometric Shapes--Congruent Triangles--Example 3
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Triangle |
|
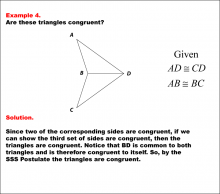
Math Example--Geometric Shapes--Congruent Triangles--Example 4 | Math Example--Geometric Shapes--Congruent Triangles--Example 4
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Triangle |
|
Math Example--Geometric Shapes--Congruent Triangles--Example 5 | Math Example--Geometric Shapes--Congruent Triangles--Example 5
This is part of a collection of math examples that focus on geometric shapes. |
Definition of a Triangle |
