IXL Ad

Illustrative Math-Media4Math Alignment

 

 

Illustrative Math Alignment: Grade 7 Unit 7

Angles, Triangles, and Prisms

Lesson 1: Relationships of Angles

Use the following Media4Math resources with this Illustrative Math lesson.

Thumbnail Image Title Body Curriculum Nodes
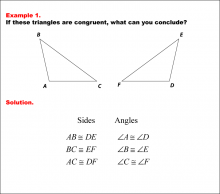
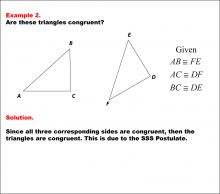
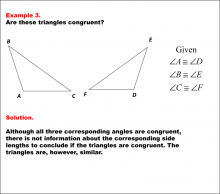
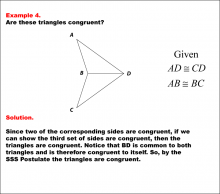
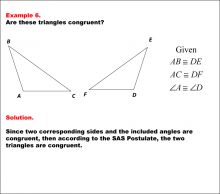
Math Example--Geometric Shapes--Congruent Triangles--Example 6 Math Example--Geometric Shapes--Congruent Triangles--Example 6 Math Example--Geometric Shapes--Congruent Triangles--Example 6

This is part of a collection of math examples that focus on geometric shapes.

 Definition of a Triangle
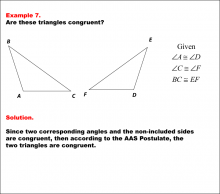
Math Example--Geometric Shapes--Congruent Triangles--Example 7 Math Example--Geometric Shapes--Congruent Triangles--Example 7 Math Example--Geometric Shapes--Congruent Triangles--Example 7

This is part of a collection of math examples that focus on geometric shapes.

 Definition of a Triangle
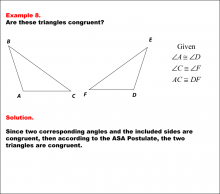
Math Example--Geometric Shapes--Congruent Triangles--Example 8 Math Example--Geometric Shapes--Congruent Triangles--Example 8 Math Example--Geometric Shapes--Congruent Triangles--Example 8

This is part of a collection of math examples that focus on geometric shapes.

 Definition of a Triangle
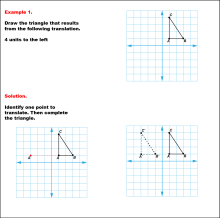
Math Example--Geometric Transformation--Translating Triangles--Example 1 Math Example--Geometric Transformation--Translating Triangles--Example 1 Math Example--Geometric Transformation--Translating Triangles--Example 1

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
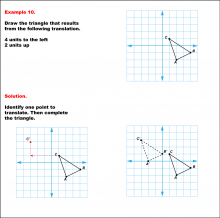
Math Example--Geometric Transformation--Translating Triangles--Example 10 Math Example--Geometric Transformation--Translating Triangles--Example 10 Math Example--Geometric Transformation--Translating Triangles--Example 10

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
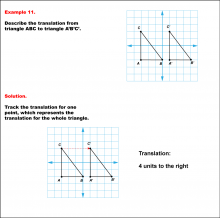
Math Example--Geometric Transformation--Translating Triangles--Example 11 Math Example--Geometric Transformation--Translating Triangles--Example 11 Math Example--Geometric Transformation--Translating Triangles--Example 11

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
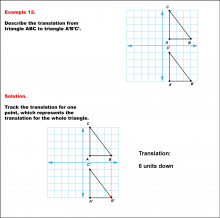
Math Example--Geometric Transformation--Translating Triangles--Example 12 Math Example--Geometric Transformation--Translating Triangles--Example 12 Math Example--Geometric Transformation--Translating Triangles--Example 12

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
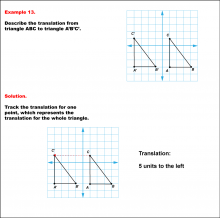
Math Example--Geometric Transformation--Translating Triangles--Example 13 Math Example--Geometric Transformation--Translating Triangles--Example 13 Math Example--Geometric Transformation--Translating Triangles--Example 13

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
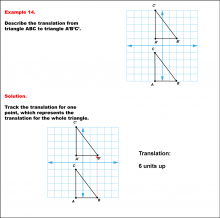
Math Example--Geometric Transformation--Translating Triangles--Example 14 Math Example--Geometric Transformation--Translating Triangles--Example 14 Math Example--Geometric Transformation--Translating Triangles--Example 14

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
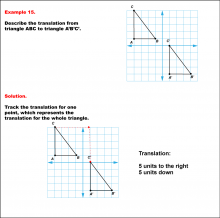
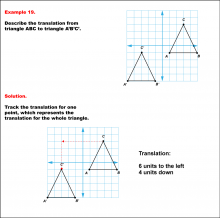
Math Example--Geometric Transformation--Translating Triangles--Example 15 Math Example--Geometric Transformation--Translating Triangles--Example 15 Math Example--Geometric Transformation--Translating Triangles--Example 15

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
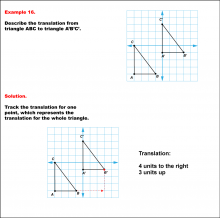
Math Example--Geometric Transformation--Translating Triangles--Example 16 Math Example--Geometric Transformation--Translating Triangles--Example 16 Math Example--Geometric Transformation--Translating Triangles--Example 16

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
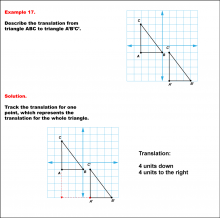
Math Example--Geometric Transformation--Translating Triangles--Example 17 Math Example--Geometric Transformation--Translating Triangles--Example 17 Math Example--Geometric Transformation--Translating Triangles--Example 17

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
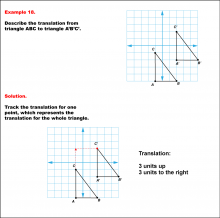
Math Example--Geometric Transformation--Translating Triangles--Example 18 Math Example--Geometric Transformation--Translating Triangles--Example 18 Math Example--Geometric Transformation--Translating Triangles--Example 18

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
Math Example--Geometric Transformation--Translating Triangles--Example 19 Math Example--Geometric Transformation--Translating Triangles--Example 19 Math Example--Geometric Transformation--Translating Triangles--Example 19

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
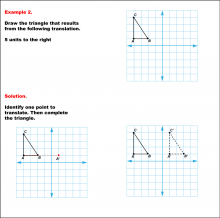
Math Example--Geometric Transformation--Translating Triangles--Example 2 Math Example--Geometric Transformation--Translating Triangles--Example 2 Math Example--Geometric Transformation--Translating Triangles--Example 2

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
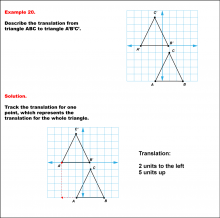
Math Example--Geometric Transformation--Translating Triangles--Example 20 Math Example--Geometric Transformation--Translating Triangles--Example 20 Math Example--Geometric Transformation--Translating Triangles--Example 20

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
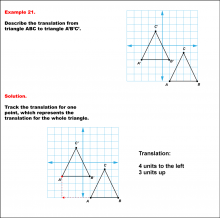
Math Example--Geometric Transformation--Translating Triangles--Example 21 Math Example--Geometric Transformation--Translating Triangles--Example 21 Math Example--Geometric Transformation--Translating Triangles--Example 21

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
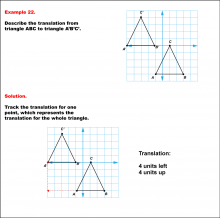
Math Example--Geometric Transformation--Translating Triangles--Example 22 Math Example--Geometric Transformation--Translating Triangles--Example 22 Math Example--Geometric Transformation--Translating Triangles--Example 22

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
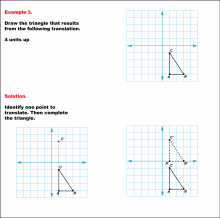
Math Example--Geometric Transformation--Translating Triangles--Example 3 Math Example--Geometric Transformation--Translating Triangles--Example 3 Math Example--Geometric Transformation--Translating Triangles--Example 3

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
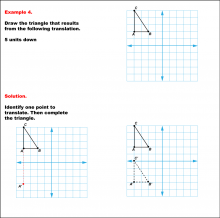
Math Example--Geometric Transformation--Translating Triangles--Example 4 Math Example--Geometric Transformation--Translating Triangles--Example 4 Math Example--Geometric Transformation--Translating Triangles--Example 4

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
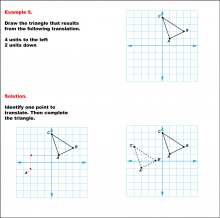
Math Example--Geometric Transformation--Translating Triangles--Example 5 Math Example--Geometric Transformation--Translating Triangles--Example 5 Math Example--Geometric Transformation--Translating Triangles--Example 5

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
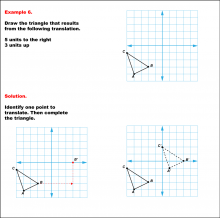
Math Example--Geometric Transformation--Translating Triangles--Example 6 Math Example--Geometric Transformation--Translating Triangles--Example 6 Math Example--Geometric Transformation--Translating Triangles--Example 6

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
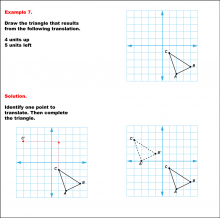
Math Example--Geometric Transformation--Translating Triangles--Example 7 Math Example--Geometric Transformation--Translating Triangles--Example 7 Math Example--Geometric Transformation--Translating Triangles--Example 7

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
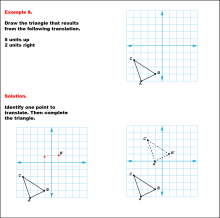
Math Example--Geometric Transformation--Translating Triangles--Example 8 Math Example--Geometric Transformation--Translating Triangles--Example 8 Math Example--Geometric Transformation--Translating Triangles--Example 8

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
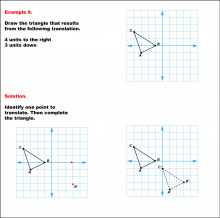
Math Example--Geometric Transformation--Translating Triangles--Example 9 Math Example--Geometric Transformation--Translating Triangles--Example 9 Math Example--Geometric Transformation--Translating Triangles--Example 9

This is part of a collection of math examples that focus on geometric transformations.

 Applications of Transformations and Applications of Triangles
Math Example--Numbers--Partitioning Rectangles: Example 1 Math Example--Numbers--Partitioning Rectangles: Example 1 Math Example--Numbers--Partitioning Rectangles: Example 1

This is part of a collection of math examples that focus on numbers and their properties.

 Identifying Shapes and Counting
Math Example--Numbers--Partitioning Rectangles: Example 2 Math Example--Numbers--Partitioning Rectangles: Example 2 Math Example--Numbers--Partitioning Rectangles: Example 2

This is part of a collection of math examples that focus on numbers and their properties.

 Identifying Shapes and Counting
Math Example--Numbers--Partitioning Rectangles: Example 3 Math Example--Numbers--Partitioning Rectangles: Example 3 Math Example--Numbers--Partitioning Rectangles: Example 3

This is part of a collection of math examples that focus on numbers and their properties.

 Identifying Shapes and Counting
Math Example--Numbers--Partitioning Rectangles: Example 4 Math Example--Numbers--Partitioning Rectangles: Example 4 Math Example--Numbers--Partitioning Rectangles: Example 4

This is part of a collection of math examples that focus on numbers and their properties.

 Identifying Shapes and Counting
Math Example--Numbers--Partitioning Rectangles: Example 5 Math Example--Numbers--Partitioning Rectangles: Example 5 Math Example--Numbers--Partitioning Rectangles: Example 5

This is part of a collection of math examples that focus on numbers and their properties.

 Identifying Shapes and Counting
Math Example--Numbers--Partitioning Rectangles: Example 6 Math Example--Numbers--Partitioning Rectangles: Example 6 Math Example--Numbers--Partitioning Rectangles: Example 6

This is part of a collection of math examples that focus on numbers and their properties.

 Identifying Shapes and Counting
Math Example--Numbers--Partitioning Rectangles: Example 7 Math Example--Numbers--Partitioning Rectangles: Example 7 Math Example--Numbers--Partitioning Rectangles: Example 7

This is part of a collection of math examples that focus on numbers and their properties.

 Identifying Shapes and Counting
Math Example--Numbers--Partitioning Rectangles: Example 8 Math Example--Numbers--Partitioning Rectangles: Example 8 Math Example--Numbers--Partitioning Rectangles: Example 8

This is part of a collection of math examples that focus on numbers and their properties.

 Identifying Shapes and Counting
Math Example--Polygons--Quadrilateral Classification: Example 1 Math Example--Polygons--Quadrilateral Classification: Example 1 Math Example--Polygons--Quadrilateral Classification: Example 1

Topic

Geometry

Description

This example presents a quadrilateral with labeled sides: AB = 5, BC = 4, CD = 3, and DA = 6. The task is to classify the quadrilateral based on these measurements. Since none of the sides are congruent and no specific relationships among the sides can be determined, this shape is classified as a generic quadrilateral.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 10 Math Example--Polygons--Quadrilateral Classification: Example 10 Math Example--Polygons--Quadrilateral Classification: Example 10

Topic

Geometry

Description

This example showcases a quadrilateral with right angles labeled with variable x at two corners, labeled as A, B, C, and D. To classify this shape, we need to solve for x: 90 + 90 + 2x = 360, which gives us x = 90. This means all angles are 90 degrees. Since opposite sides are parallel and congruent, we can classify this shape as a rectangle.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 11 Math Example--Polygons--Quadrilateral Classification: Example 11 Math Example--Polygons--Quadrilateral Classification: Example 11

Topic

Geometry

Description

This example presents a square with all sides congruent and right angles, labeled as A, B, C, and D. The task is to classify the quadrilateral based on these characteristics. As all interior angles are 90 degrees and all sides are congruent, this shape is confirmed to be a square.

 Definition of a Quadrilateral
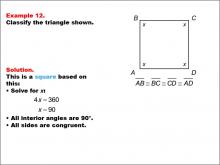
Math Example--Polygons--Quadrilateral Classification: Example 12 Math Example--Polygons--Quadrilateral Classification: Example 12 Math Example--Polygons--Quadrilateral Classification: Example 12

Topic

Geometry

Description

This example features a quadrilateral with all sides labeled x and marked congruent, labeled as A, B, C, and D. To classify this shape, we need to solve for x: 4x = 360, which gives us x = 90. This means all angles are 90 degrees. Since all sides are congruent and all angles are right angles, we can classify this shape as a square.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 13 Math Example--Polygons--Quadrilateral Classification: Example 13 Math Example--Polygons--Quadrilateral Classification: Example 13

Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with all sides marked as congruent and angles marked as right angles. The side lengths are indicated with x. To classify this shape, we solve for x: 90 + 90 + 2x = 360, which gives us x = 90. This confirms that all interior angles are 90 degrees. Since all sides are congruent and all angles are right angles, we can classify this shape as a square.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 14 Math Example--Polygons--Quadrilateral Classification: Example 14 Math Example--Polygons--Quadrilateral Classification: Example 14

Topic

Geometry

Description

This example showcases a quadrilateral labeled ABCD with all sides marked as congruent and angles marked as right angles. Each side is labeled with a length of 1. Based on these characteristics, we can classify this shape as a square. All sides are congruent, which means opposite sides are parallel. Angle ABC is 90 degrees, and its adjacent angles are supplementary, confirming that all interior angles are 90 degrees.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 15 Math Example--Polygons--Quadrilateral Classification: Example 15 Math Example--Polygons--Quadrilateral Classification: Example 15

Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with all sides marked as congruent and angles marked as right angles. The side lengths are indicated with x. Based on these characteristics, we can classify this shape as a square. Because all sides are congruent, opposite sides are parallel. Angle ABC is 90 degrees, and its adjacent angles are supplementary, confirming that all interior angles are 90 degrees.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 16 Math Example--Polygons--Quadrilateral Classification: Example 16 Math Example--Polygons--Quadrilateral Classification: Example 16

Topic

Geometry

Description

This example features a quadrilateral labeled ABCD with two sides labeled with lengths of 5 and x, and angles marked as right angles. The diagram shows perpendicular lines and parallel lines. Based on these characteristics, we can classify this shape as a square. Because angle ABC and angle BAD are supplementary, BC and AD are parallel. Since AB and CD are congruent, angle BAD and angle ADC are supplementary. Therefore, all interior angles are 90 degrees, and all sides are congruent.

 Definition of a Quadrilateral
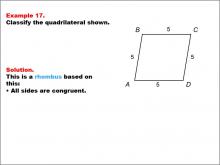
Math Example--Polygons--Quadrilateral Classification: Example 17 Math Example--Polygons--Quadrilateral Classification: Example 17 Math Example--Polygons--Quadrilateral Classification: Example 17

Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with all sides marked as 5 units, indicating congruence. Based on this characteristic, we can classify this shape as a rhombus. The key property that defines a rhombus is that all sides are congruent, which is clearly demonstrated in this example.

 Definition of a Quadrilateral
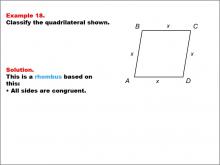
Math Example--Polygons--Quadrilateral Classification: Example 18 Math Example--Polygons--Quadrilateral Classification: Example 18 Math Example--Polygons--Quadrilateral Classification: Example 18

Topic

Geometry

Description

This example showcases a quadrilateral labeled ABCD with all sides marked as x, indicating congruence. Based on this characteristic, we can classify this shape as a rhombus. The defining property of a rhombus is that all sides are congruent, which is clearly demonstrated in this example by using the variable x for all side lengths.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 19 Math Example--Polygons--Quadrilateral Classification: Example 19 Math Example--Polygons--Quadrilateral Classification: Example 19

Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with sides AB and CD marked as x, and BC and AD marked as 5. Opposite sides are noted to be parallel. Based on these characteristics, we can classify this shape as a rhombus. The key properties that define this as a rhombus are: opposite sides are parallel, and opposite sides are congruent. Since x = 5, all sides are congruent, which is a defining property of a rhombus.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 2 Math Example--Polygons--Quadrilateral Classification: Example 2 Math Example--Polygons--Quadrilateral Classification: Example 2

Topic

Geometry

Description

This example showcases a quadrilateral with sides labeled as variables: x, y, z, and w. The task is to classify the quadrilateral based on this information. As no specific relationships between the sides are given, and no sides are stated to be congruent, this shape is classified as a generic quadrilateral.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 20 Math Example--Polygons--Quadrilateral Classification: Example 20 Math Example--Polygons--Quadrilateral Classification: Example 20

Topic

Geometry

Description

This example features a quadrilateral labeled ABCD with angles B and D marked as 120 degrees, and angles A and C as 60 degrees. Sides AB and BC are marked as congruent. Based on these characteristics, we can classify this shape as a rhombus. All pairs of adjacent angles are supplementary (120° + 60° = 180°), which means opposite sides are parallel. Since AB is congruent to BC, and opposite sides are congruent in a parallelogram, all sides must be congruent, defining this shape as a rhombus.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 21 Math Example--Polygons--Quadrilateral Classification: Example 21 Math Example--Polygons--Quadrilateral Classification: Example 21

Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with sides marked as x and y. The opposite sides are noted to be congruent, and there's an additional note indicating AB is congruent to BC. Based on these characteristics, we can classify this shape as a rhombus. Both pairs of opposite angles are congruent, which means opposite sides are parallel. Since AB is congruent to BC, and opposite sides are congruent, all sides must be congruent, defining this shape as a rhombus.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 22 Math Example--Polygons--Quadrilateral Classification: Example 22 Math Example--Polygons--Quadrilateral Classification: Example 22

Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with angles marked as 70° and sides marked as x. Opposite angles are noted to be congruent, and there's an additional note indicating AB is congruent to BC. Based on these characteristics, we can classify this shape as a rhombus. Both pairs of opposite angles are congruent, which means opposite sides are parallel. Since AB is congruent to BC, and opposite sides are congruent in a parallelogram, all sides must be congruent, defining this shape as a rhombus.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 23 Math Example--Polygons--Quadrilateral Classification: Example 23 Math Example--Polygons--Quadrilateral Classification: Example 23

Topic

Geometry

Description

This example features a quadrilateral labeled ABCD with angles marked as 120° and 80°. Opposite angles are noted to be congruent. Based on these characteristics, we can classify this shape as a parallelogram. Both pairs of opposite angles are congruent, which means opposite sides are parallel, a defining property of parallelograms.

 Definition of a Quadrilateral
Math Example--Polygons--Quadrilateral Classification: Example 24 Math Example--Polygons--Quadrilateral Classification: Example 24 Math Example--Polygons--Quadrilateral Classification: Example 24

Topic

Geometry

Description

This example presents a quadrilateral labeled ABCD with sides marked as x and y. The opposite sides are noted to be congruent. Based on these characteristics, we can classify this shape as a parallelogram. Both pairs of opposite sides are congruent, which means opposite sides are parallel, a defining property of parallelograms.

 Definition of a Quadrilateral