Illustrative Math Alignment: Grade 7 Unit 9

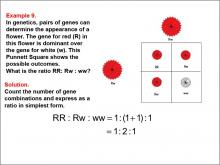
Topic

Ratios and Rates

Description

This example introduces the concept of ratios in genetics using a Punnett square. The image shows genetic combinations for a flower's color, including RR, Rw, and ww, with corresponding images of red and white flowers. Students are asked to determine the ratio of different gene combinations.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to solve a proportion problem where two ratios a:b and c:d are proportional. Given the values b = 3, c = 4, and d = 6, we need to find the value of a. The proportion is set up as a / 3 = 4 / 6, which is then solved to find that a = 2.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar triangles with algebraic expressions. Two triangles are shown, one with sides of 6 and 9, and the other with sides of 2x and 2x + 9. The problem requires setting up a proportion: 6 / 9 = 2x / (2x + 9). Solving this equation leads to x = 9, which then allows us to find the side lengths of 18 and 27.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, one with legs of 7 and 9, and the other with legs of 14 and x. The problem requires finding the length of side x by setting up a proportion based on the similar triangles: 7 / 9 = 14 / x. Solving this equation leads to x = 18.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, one with legs of 5 and 8, and the other with legs of 2x and (2x + 6). The problem requires setting up a proportion: 5 / 8 = 2x / (2x + 6). Solving this equation leads to x = 5, which then allows us to find the side lengths of 10 and 16.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°). Two triangles are shown, with the smaller one having sides of 6√3 and 6, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: (6√3) / 6 = x / 12. Solving this equation leads to x = 12√3.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°) and algebraic expressions. Two triangles are shown, with the smaller one having sides of 16 and 8, and the larger one having sides of (3x + 4) and 2x. The problem requires setting up a proportion: 16 / 8 = (3x + 4) / 2x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 8 and 16.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the smaller one having sides of 4 and 3, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: 4 / 3 = x / 12. Solving this equation leads to x = 16.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the smaller one having sides of (3x + 4) and 6, and the larger one having sides of 3x and 3x. The problem requires setting up a proportion: 8 / 6 = (3x + 4) / 3x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 12 and 16.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 12 / 5 = x / 15. Solving this equation leads to x = 36.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of 10x + 8 and 5x. The problem requires setting up a proportion: 12 / 5 = (10x + 8) / 5x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 20 and 48.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar isosceles right triangles. Two 45-45-90 triangles are shown, with one having sides labeled y and 5√2, and the other having sides labeled x and 12. The problem requires finding the lengths of both x and y using the special properties of isosceles right triangles and proportions.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion where b is expressed as x + 1, and c and d are given constants (c = 3, d = 2). The goal is to solve for a using the proportion a / b = c / d. By substituting the known values, we set up the equation a / (x + 1) = 3 / 2 and solve for a, resulting in the expression a = (3(x + 1)) / 2.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar isosceles right triangles with algebraic expressions. Two 45-45-90 triangles are shown, with one having sides labeled 15√2 and 15, and the other having sides labeled √2 * 5x and y. The problem requires finding the length of y in terms of x using the special properties of isosceles right triangles and proportions.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar isosceles triangles. Two isosceles triangles are shown, with the smaller one having sides of 30 and 16, and the larger one having sides of x and 20. The problem requires finding the length of side x by setting up a proportion: 30 / 16 = x / 20. Solving this equation leads to x = 37.5.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar isosceles triangles with algebraic expressions. Two isosceles triangles are shown, with the smaller one having sides of 22 and 12, and the larger one having sides of 10x + 5 and 6x. The problem requires setting up a proportion: 22 / 12 = (10x + 5) / 6x. Solving this equation leads to x = 5, which then allows us to find the side lengths of the larger triangle.

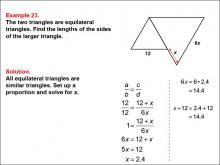
Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar equilateral triangles. Two equilateral triangles are shown, with the smaller one having a side length of 12, and the larger one having a side length of 6x and an additional side labeled as 12 + x. The problem requires finding the lengths of the sides of the larger triangle by setting up a proportion: 12 / 12 = (12 + x) / 6x. Solving this equation leads to x = 2.4, and the length of the larger triangle's side is found to be approximately 14.4 units.

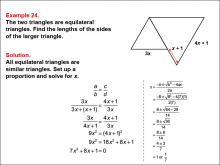
Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a complex proportion problem using similar equilateral triangles with algebraic expressions. Two equilateral triangles are shown, with the smaller one having a side length of 3x, and the larger one having side lengths labeled as (4x + 1) and (x + 1). The problem requires setting up a proportion: 3x / (4x + 1) = 3x / (3x + (x + 1)). Solving this equation leads to a quadratic equation, which when solved gives x ≈ 7/1.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar rectangles. Two rectangles are shown, with the smaller one having sides of 2 and 3, and the larger one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 2 / 3 = x / 15. Solving this equation leads to x = 10.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar rectangles with algebraic expressions. Two rectangles are shown, with the smaller one having sides of 5 and 12, and the larger one having sides of x + 5 and 3x + 6. The problem requires setting up a proportion: 5 / 12 = (x + 5) / (3x + 6). Solving this equation leads to x = 10, which then allows us to find the side lengths of the larger rectangle as 15 and 36.

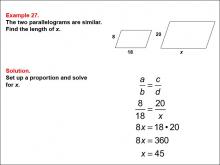
Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar parallelograms. Two parallelograms are shown, with the smaller one having sides of 8 and 18, and the larger one having sides of 20 and x. The problem requires finding the length of side x by setting up a proportion: 8 / 18 = 20 / x. Solving this equation leads to x = 45.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar parallelograms with algebraic expressions. Two parallelograms are shown, with the smaller one having sides of 9 and 21, and the larger one having sides of x + 12 and 4x + 3. The problem requires setting up a proportion: 9 / 21 = (x + 12) / (4x + 3). Solving this equation leads to x = 15, which then allows us to find the side lengths of the larger parallelogram as 27 and 63.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two triangles are similar using proportions. Two triangles are shown, both with a 70° angle. The first triangle has sides of 12 and 10, while the second has sides of 18 and 15. The problem requires setting up a proportion to check for similarity: 12 / 10 = 18 / 15. After simplifying, both ratios are equal (6 / 5 = 6 / 5), confirming that the triangles are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving for b in a proportion where a = 8, c = 4, and d = 3. We set up the proportion 8 / b = 4 / 3 and solve for b, resulting in b = 6. This problem shows how to find an unknown value in the denominator of a proportion.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates how to determine if two triangles are not similar using proportions. Two triangles are shown, both with a 75° angle. The first triangle has sides of 15 and 9, while the second has sides of 28 and 18. The problem requires setting up a proportion to check for similarity: 15 / 9 = 28 / 18. After simplifying, the ratios are not equal (5 / 3 ≠ 14 / 9), concluding that the triangles are not similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two right triangles are similar using proportions. Two right triangles are shown, one with legs of length 4 and 3, and the other with legs of length 10 and 7.5. The problem requires setting up a proportion to check for similarity: 4 / 3 = 10 / 7.5. After simplifying, both ratios are equal (4 / 3 = 4 / 3), confirming that the triangles are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates how to determine if two right triangles are not similar using proportions. Two right triangles are shown, one with legs of length 12 and 5, and the other with legs of length 35 and 15. The problem requires setting up a proportion to check for similarity: 12 / 5 = 35 / 15. After simplifying, the ratios are not equal (12 / 5 ≠ 7 / 3), concluding that the triangles are not similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two rectangles are similar using proportions. Two rectangles are shown, with the first having dimensions 3 and 8, and the second having dimensions 9 and 24. The problem requires setting up a proportion to check for similarity: 3 / 8 = 9 / 24. After simplifying, the ratios are equal, confirming that the rectangles are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates how to determine if two rectangles are similar using proportions with algebraic expressions. Two rectangles are shown, with the first having dimensions 11.5 and 23, and the second having dimensions 23x and 46x. The problem requires setting up a proportion to check for similarity: 11.5 / 23 = 23x / 46x. After simplifying, the ratios are equal, confirming that the rectangles are indeed similar for any value of x.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two parallelograms are similar using proportions. Two parallelograms are shown, with the first having dimensions 6 and 9, and the second having dimensions 15 and 22.5. The problem requires setting up a proportion to check for similarity: 6 / 9 = 15 / 22.5. After simplifying, the ratios are equal, confirming that the parallelograms are indeed similar.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates how to determine if two parallelograms are not similar using proportions. Two parallelograms are shown, with the first having dimensions 9 and 28, and the second having dimensions 18 and 54. The problem requires setting up a proportion to check for similarity: 9 / 18 ≠ 28 / 54. After simplifying, the ratios are not equal, concluding that the parallelograms are not similar.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar triangles with algebraic expressions. Two triangles are shown, one with side lengths 9 and 18, and the other with expressions 6x and 10x + 6. The problem requires setting up a proportion to determine the value of x for which the triangles are similar: 9 / 18 = 6x / (10x + 6). Solving this equation leads to x = 3.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, one with side lengths 4 and 3, and the other with expressions 3x and 2x + 1. The problem requires setting up a proportion to determine the value of x for which the triangles are similar: 4 / 3 = 3x / (2x + 1). Solving this equation leads to x = 4.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving a proportion problem using similar rectangles with an unknown side length. Two rectangles are shown, one with side lengths of 4 and x, and the other with side lengths of 15 and 4. The problem requires setting up a proportion to determine the value of x for which the rectangles are similar: 4 / 15 = x / 4. Solving this equation leads to x = 16/15.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving for b in a proportion where a is expressed as x + 2, and c and d are given constants (c = 5, d = 2). We set up the equation (x + 2) / b = 5 / 2 and solve for b, resulting in the expression b = (2(x + 2)) / 5. This problem demonstrates how to handle algebraic expressions in proportions.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar parallelograms with algebraic expressions. Two parallelograms are shown, one with side lengths of 6 and x, and the other with expressions of 3x + 2 and 22. The problem requires setting up a proportion to determine the value of x for which the parallelograms are similar: 6 / 22 = x / (3x + 2). Solving this equation leads to x = 3.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving for c in a proportion where a = 9, b = 4, and d = 12. We set up the proportion 9 / 4 = c / 12 and solve for c, resulting in c = 27. This problem shows how to find an unknown value in the numerator of a proportion.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving for c in a proportion where a = 8, b = 3, and d is expressed as x + 3. We set up the equation 8 / 3 = c / (x + 3) and solve for c, resulting in the expression c = (8(x + 3)) / 3. This problem demonstrates how to handle algebraic expressions in the denominator of a proportion.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving for d in a proportion where a = 12, b = 5, and c = 48. We set up the proportion 12 / 5 = 48 / d and solve for d, resulting in d = 20. This problem shows how to find an unknown value in the denominator of a proportion when all other values are known.

Topic

Ratios, Proportions, and Percents

Description

This example illustrates solving for d in a proportion where a = 11, b = 5, and c is expressed as x - 4. We set up the equation 11 / 5 = (x - 4) / d and solve for d, resulting in the expression d = (5(x - 4)) / 11. This problem demonstrates how to handle algebraic expressions in the numerator of a proportion.

Topic

Ratios, Proportions, and Percents

Description

This example demonstrates solving a proportion problem using similar triangles. Two triangles are shown, with one having sides of 3 and 4, and the other having sides of 6 and x. The problem requires finding the length of side x by setting up a proportion based on the similar triangles: 3 / 4 = 6 / x. Solving this equation leads to x = 8.

November 2014. In this issue of Math in the News we examine the historic landing of a spacecraft on an asteroid in space.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

August 2016. In this issue of Math in the News calculate average speed to various vacation destinations when traveling by car.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

September 2016. In this issue of Math in the News, we look at back-to-school purchases and the impact that different tax rates have on the total cost.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

December 2022. In this issue of Math in the News we look at box office hits and misses from Disney. The House of Blockbosters every now and then misfires. It's useful to analyze box office data to see what we can learn from the hits and misses. 

Note: The download is a PPT file.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

6/6/11. In this issue we look at the technology of Doppler Radar and explore its underlying mathematical structure.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

February 2023. In this issue of Math in the News we look at NFL statistics for the number of concussions. The NFL now tracks concussion, and this is an opportunity to analyze this data and draw conclusions.

Note: The download is a PPT file.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

8/22/11. In this issue we look at the way in which the U.S. government borrows money. This involves an exploration of Treasury bonds and notes.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

February 2012. In this issue we look at unemployment statistics from the Bureau of Labor Statistics.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

4/18/11. In this issue we look at income taxes. We analyze who pays what proportion of income taxes based on income level.

Related Resources

To see resources related to this topic click on the Related Resources tab above.