
Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 10: Measuring Long Distances Over Uneven Terrain
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Example--Percents--Equations with Percents: Example 31 | Math Example--Percents--Equations with Percents: Example 31TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "4 is 0.1% of what number?" The solution involves setting up the equation 4 = 0.001 * x, then solving for x to get x = 4 / 0.001, which equals 4000. This example demonstrates how to calculate the whole when given a very small percentage of it, resulting in a much larger number. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 32 | Math Example--Percents--Equations with Percents: Example 32TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "7 is 1% of what number?" The solution involves setting up the equation 7 = 0.01 * x, then solving for x to get x = 7 / 0.01, which equals 700. This example introduces a scenario where we need to find the whole when given a small percentage of it, resulting in a number 100 times larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 33 | Math Example--Percents--Equations with Percents: Example 33TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "9 is 30% of what number?" The solution involves setting up the equation 9 = 0.3 * x, then solving for x to get x = 9 / 0.3, which equals 30. This example demonstrates how to calculate the whole when given a larger percentage of it, resulting in a number that is only slightly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 34 | Math Example--Percents--Equations with Percents: Example 34TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "1 is 400% of what number?" The solution involves setting up the equation 1 = 4.0 * x, then solving for x to get x = 1 / 4, which equals 0.25. This example introduces a scenario where we need to find a number that, when increased by 400%, results in 1, leading to a fraction or decimal less than 1. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 35 | Math Example--Percents--Equations with Percents: Example 35TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "15 is 0.25% of what number?" The solution involves setting up the equation 15 = 0.0025 * x, then solving for x to get x = 15 / 0.0025, which equals 6000. This example introduces a scenario where we need to find the whole when given a very small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 36 | Math Example--Percents--Equations with Percents: Example 36TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "30 is 5% of what number?" The solution involves setting up the equation 30 = 0.05 * x, then solving for x to get x = 30 / 0.05, which equals 600. This example demonstrates how to calculate the whole when given a small percentage of it, resulting in a much larger number. |
Solving Percent Equations |
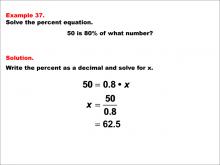
|
Math Example--Percents--Equations with Percents: Example 37 | Math Example--Percents--Equations with Percents: Example 37TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "50 is 80% of what number?" The solution involves setting up the equation 50 = 0.8 * x, then solving for x to get x = 50 / 0.8, which equals 62.5. This example introduces a scenario where we need to find the whole when given a large percentage of it, resulting in a number that is only slightly larger than the given value. |
Solving Percent Equations |
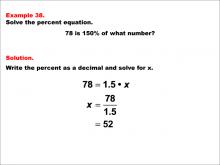
|
Math Example--Percents--Equations with Percents: Example 38 | Math Example--Percents--Equations with Percents: Example 38TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "78 is 150% of what number?" The solution involves setting up the equation 78 = 1.5 * x, then solving for x to get x = 78 / 1.5, which equals 52. This example demonstrates how to calculate the original value when given a percentage greater than 100%, resulting in a number that is smaller than the given value. |
Solving Percent Equations |
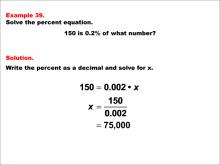
|
Math Example--Percents--Equations with Percents: Example 39 | Math Example--Percents--Equations with Percents: Example 39TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "150 is 0.2% of what number?" The solution involves setting up the equation 150 = 0.002 * x, then solving for x to get x = 150 / 0.002, which equals 75,000. This example introduces a scenario where we need to find the whole when given a very small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 4 | Math Example--Percents--Equations with Percents: Example 4TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 6.5% of 45.5?" The solution involves converting 6.5% to its decimal equivalent, 0.065, and then multiplying it by 45.5 to obtain the result of 2.9575. This example introduces both a decimal percentage and a decimal base number, adding complexity to the calculation. |
Solving Percent Equations |
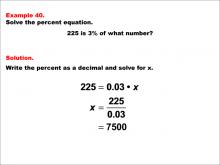
|
Math Example--Percents--Equations with Percents: Example 40 | Math Example--Percents--Equations with Percents: Example 40TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "225 is 3% of what number?" The solution involves setting up the equation 225 = 0.03 * x, then solving for x to get x = 225 / 0.03, which equals 7,500. This example demonstrates how to calculate the whole when given a small percentage of it, resulting in a number that is significantly larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 41 | Math Example--Percents--Equations with Percents: Example 41TopicSolving Equations DescriptionThis math example focuses on solving percent equations by asking "400 is 40% of what number?" The solution involves setting up the equation 400 = 0.4 * x, then solving for x to get x = 400 / 0.4, which equals 1000. This example demonstrates how to calculate the whole when given a significant percentage of it, resulting in a number that is larger than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 42 | Math Example--Percents--Equations with Percents: Example 42TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "650 is 130% of what number?" The solution involves setting up the equation 650 = 1.3 * x, then solving for x to get x = 650 / 1.3, which equals 500. This example introduces a scenario where we need to find the original value when given a percentage greater than 100%, resulting in a number that is smaller than the given value. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 5 | Math Example--Percents--Equations with Percents: Example 5TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 30% of 9?" The solution involves converting 30% to its decimal form, 0.3, and then multiplying it by 9 to get the result of 2.7. This example introduces a larger percentage, demonstrating how the method applies consistently across various percentage values. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 6 | Math Example--Percents--Equations with Percents: Example 6TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 28% of 7.2?" The solution involves converting 28% to its decimal equivalent, 0.28, and then multiplying it by 7.2 to obtain the result of 2.016. This example combines a whole number percentage with a decimal base number, further illustrating the versatility of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 7 | Math Example--Percents--Equations with Percents: Example 7TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 45% of 68?" The solution involves converting 45% to its decimal form, 0.45, and then multiplying it by 68 to arrive at the answer of 30.6. This example introduces a larger percentage and a larger whole number as the base value, demonstrating the scalability of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 8 | Math Example--Percents--Equations with Percents: Example 8TopicSolving Equations DescriptionThis math example demonstrates solving percent equations by asking "What is 52.3% of 36.9?" The solution involves converting 52.3% to its decimal equivalent, 0.523, and then multiplying it by 36.9 to obtain the result of 19.2987. This example introduces both a decimal percentage and a decimal base number, adding complexity to the calculation and showcasing the versatility of the percent-to-decimal conversion method. |
Solving Percent Equations |

|
Math Example--Percents--Equations with Percents: Example 9 | Math Example--Percents--Equations with Percents: Example 9TopicSolving Equations DescriptionThis math example focuses on solving percent equations, specifically asking "What is 150% of 8?" The solution involves converting 150% to its decimal form, 1.5, and then multiplying it by 8 to get the result of 12. This example introduces a percentage greater than 100%, demonstrating how the method applies consistently even when dealing with percentages that represent values larger than the whole. |
Solving Percent Equations |

|
Math Example--Percents--Percent Change--Example 1 | Math Example--Percents--Percent Change--Example 1
This is part of a collection of math examples that focus on percents. |
Percents |

|
Math Example--Percents--Percent Change--Example 10 | Math Example--Percents--Percent Change--Example 10
This is part of a collection of math examples that focus on percents. |
Percents |

|
Math Example--Percents--Percent Change--Example 2 | Math Example--Percents--Percent Change--Example 2
This is part of a collection of math examples that focus on percents. |
Percents |

|
Math Example--Percents--Percent Change--Example 3 | Math Example--Percents--Percent Change--Example 3
This is part of a collection of math examples that focus on percents. |
Percents |

|
Math Example--Percents--Percent Change--Example 4 | Math Example--Percents--Percent Change--Example 4
This is part of a collection of math examples that focus on percents. |
Percents |

|
Math Example--Percents--Percent Change--Example 5 | Math Example--Percents--Percent Change--Example 5
This is part of a collection of math examples that focus on percents. |
Percents |

|
Math Example--Percents--Percent Change--Example 6 | Math Example--Percents--Percent Change--Example 6
This is part of a collection of math examples that focus on percents. |
Percents |

|
Math Example--Percents--Percent Change--Example 7 | Math Example--Percents--Percent Change--Example 7
This is part of a collection of math examples that focus on percents. |
Percents |

|
Math Example--Percents--Percent Change--Example 8 | Math Example--Percents--Percent Change--Example 8
This is part of a collection of math examples that focus on percents. |
Percents |

|
Math Example--Percents--Percent Change--Example 9 | Math Example--Percents--Percent Change--Example 9
This is part of a collection of math examples that focus on percents. |
Percents |
|
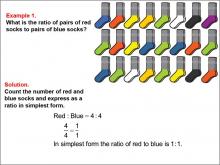
Math Example--Ratios and Rates--Example 1 | Math Example--Ratios and Rates--Example 1TopicRatios and Rates DescriptionThis math example focuses on understanding ratios using colored socks. The image displays a collection of red and blue socks, and students are asked to determine the ratio of red socks to blue socks. The solution demonstrates that there are 4 pairs of red socks and 4 pairs of blue socks, resulting in a ratio of 4 : 4, which simplifies to 1 : 1. |
Ratios and Rates |
|
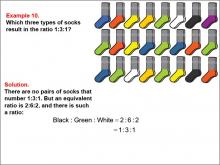
Math Example--Ratios and Rates--Example 10 | Math Example--Ratios and Rates--Example 10TopicRatios and Rates DescriptionThis example focuses on finding equivalent ratios using a collection of socks in various colors. The image shows socks arranged in rows, with black, green, white, and other colors present. Students are asked to find a ratio among three colors that is equivalent to 1 : 3 : 1. |
Ratios and Rates |
|
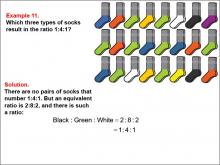
Math Example--Ratios and Rates--Example 11 | Math Example--Ratios and Rates--Example 11TopicRatios and Rates DescriptionThis example focuses on finding equivalent ratios using a collection of socks in various colors. The image shows socks arranged in rows, with black, green, white, and other colors present. Students are asked to find a ratio among three colors that is equivalent to 1 : 4 : 1. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 12 | Math Example--Ratios and Rates--Example 12TopicRatios and Rates DescriptionThis example explores the concept of similar triangles using ratios. The image shows a right triangle with sides labeled as 9, 12, and 15 units. Students are asked to determine if this triangle is similar to a standard 3-4-5 Pythagorean triplet triangle. Understanding similar triangles is an important application of ratios in geometry. This example demonstrates how ratios can be used to compare the sides of triangles and determine similarity. By scaling the sides of a known triangle (3-4-5) and comparing them to the given triangle, students can see how ratios maintain proportionality in similar shapes. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 13 | Math Example--Ratios and Rates--Example 13TopicRatios and Rates DescriptionThis example focuses on verifying the similarity of triangles using ratios. The image shows a right triangle with sides labeled 25, 60, and 65 units. Students are guided through a step-by-step process to determine if this triangle is similar to a 5-12-13 right triangle. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 14 | Math Example--Ratios and Rates--Example 14TopicRatios and Rates DescriptionThis example explores the concept of special right triangles using ratios. The image shows a right triangle with sides labeled 3, 3 2 2 , and 6 units. Students are guided through a step-by-step process to verify if this triangle is similar to a 30°-60°-90° triangle. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 15 | Math Example--Ratios and Rates--Example 15TopicRatios and Rates |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 16 | Math Example--Ratios and Rates--Example 16TopicRatios and Rates DescriptionThis example focuses on converting units of speed and calculating rates. The image shows a car and calculations for converting speed from miles per hour to feet per second, given the distance traveled in miles and time in minutes. Understanding unit conversions and rate calculations is crucial in many real-world applications, particularly in physics and engineering. This example demonstrates how to use ratios to convert between different units of speed, showcasing the practical application of mathematical concepts in everyday scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 17 | Math Example--Ratios and Rates--Example 17TopicRatios and Rates DescriptionThis example explores the concept of unit rates using the cost of gasoline. The image shows a red gasoline container, and students are asked to calculate the cost per gallon of gas given the total cost and volume. Understanding unit rates is a fundamental skill in mathematics with numerous real-world applications. This example demonstrates how to calculate a unit rate by dividing the total cost by the total quantity, illustrating the practical use of division in everyday scenarios like purchasing gasoline. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 18 | Math Example--Ratios and Rates--Example 18TopicRatios and Rates DescriptionThis example focuses on calculating unit rates in a restaurant context. The image shows a hamburger, and students are asked to determine the cost per pound of ground beef given the total cost and weight purchased. Understanding unit rates is essential in various real-world scenarios, particularly in business and economics. This example illustrates how to calculate a unit rate by dividing the total cost by the total quantity, demonstrating the practical application of division in a restaurant supply context. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 19 | Math Example--Ratios and Rates--Example 19TopicRatios and Rates DescriptionThis example explores the concept of flow rates using a backyard pool scenario. The image shows a backyard pool, and students are asked to calculate the rate of water flow in gallons per minute given the pool's capacity and the time taken to fill it. Understanding flow rates is important in various fields, including engineering and physics. This example demonstrates how to calculate a rate by dividing the total volume by the total time, illustrating the practical application of division in real-world scenarios involving fluid dynamics. |
Ratios and Rates |
|
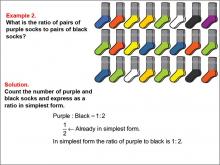
Math Example--Ratios and Rates--Example 2 | Math Example--Ratios and Rates--Example 2TopicRatios and Rates DescriptionThis example explores ratios using purple and black socks. The image shows a collection of socks, and students are asked to determine the ratio of purple socks to black socks. The solution reveals that there is 1 pair of purple socks and 2 pairs of black socks, resulting in a ratio of 1 : 2, which is already in its simplest form. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 20 | Math Example--Ratios and Rates--Example 20TopicRatios and Rates DescriptionThis example focuses on unit conversion using the height of the Statue of Liberty. The image shows the Statue of Liberty, and students are asked to convert its height from feet to inches. Understanding unit conversions is crucial in many fields, including science, engineering, and everyday life. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in real-world measurement scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 21 | Math Example--Ratios and Rates--Example 21TopicRatios and Rates DescriptionThis example focuses on unit conversion, specifically converting the height of the Statue of Liberty from feet to yards. The image shows the iconic Statue of Liberty, providing a real-world context for the mathematical problem. Understanding unit conversions is crucial in many fields, including engineering, science, and everyday life. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of division and multiplication in real-world measurement scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 22 | Math Example--Ratios and Rates--Example 22TopicRatios and Rates DescriptionThis example explores unit conversion, specifically converting the height of the Statue of Liberty from feet to miles. The image depicts the Statue of Liberty, providing a tangible reference for the mathematical problem. Understanding unit conversions, especially between widely different scales like feet and miles, is important in various fields such as geography, engineering, and urban planning. This example showcases how to use a conversion factor to change units, demonstrating the practical application of division and multiplication in real-world measurement scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 23 | Math Example--Ratios and Rates--Example 23TopicRatios and Rates DescriptionThis example focuses on unit conversion, specifically converting the height of columns from inches to feet. The image shows columns, providing a visual context for the mathematical problem. Understanding unit conversions between inches and feet is crucial in many practical applications, including construction, interior design, and everyday measurements. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of division and multiplication in real-world measurement scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 24 | Math Example--Ratios and Rates--Example 24TopicRatios and Rates DescriptionThis example explores unit conversion in a sports context, specifically converting a quarterback's pass distance from yards to feet. The image shows a silhouette of a quarterback throwing a football, providing a real-world scenario for the mathematical problem. Understanding unit conversions between yards and feet is crucial in many sports, especially American football. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in sports-related measurement scenarios. |
Ratios and Rates |
|
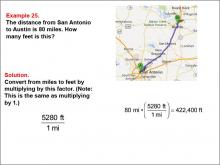
Math Example--Ratios and Rates--Example 25 | Math Example--Ratios and Rates--Example 25TopicRatios and Rates DescriptionThis example focuses on unit conversion in a geographic context, specifically converting the distance between San Antonio and Austin from miles to feet. The image shows a map of the route between these two Texas cities, providing a real-world scenario for the mathematical problem. Understanding unit conversions between miles and feet is important in various fields, including geography, transportation, and urban planning. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in distance-related measurement scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 26 | Math Example--Ratios and Rates--Example 26TopicRatios and Rates DescriptionThis example focuses on time unit conversion, specifically converting hours to minutes in the context of a standardized test duration. The image shows a clock, providing a visual representation of time for the mathematical problem. Understanding time unit conversions is crucial in many aspects of daily life, including scheduling, time management, and test-taking. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of multiplication in time-related scenarios. |
Ratios and Rates |
|
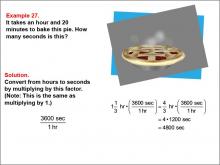
Math Example--Ratios and Rates--Example 27 | Math Example--Ratios and Rates--Example 27TopicRatios and Rates DescriptionThis example explores time unit conversion, specifically converting hours and minutes to seconds in the context of baking a pie. The image shows a steaming pie, providing a real-world scenario for the mathematical problem. Understanding time unit conversions, especially when dealing with mixed units, is important in various fields such as cooking, manufacturing, and project management. This example demonstrates how to use conversion factors to change units, illustrating the practical application of multiplication in time-related scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 28 | Math Example--Ratios and Rates--Example 28TopicRatios and Rates DescriptionThis example focuses on time unit conversion in a sports context, specifically converting minutes and seconds to seconds for a horse race lap time. The image shows a horse, providing a visual context for the mathematical problem. Understanding time unit conversions is crucial in many sports, especially those involving racing and timed events. This example demonstrates how to use conversion factors to change units and add different time units, illustrating the practical application of multiplication and addition in sports-related time scenarios. |
Ratios and Rates |

|
Math Example--Ratios and Rates--Example 29 | Math Example--Ratios and Rates--Example 29TopicRatios and Rates DescriptionThis example explores time unit conversion in an IT context, specifically converting seconds to minutes for user session duration. The image shows a computer tower, providing a real-world scenario for the mathematical problem. Understanding time unit conversions is crucial in many technological fields, especially in IT and user experience analysis. This example demonstrates how to use a conversion factor to change units, illustrating the practical application of division in time-related measurement scenarios. It also introduces the concept of mixed numbers in the result. |
Ratios and Rates |