Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 10: Measuring Long Distances Over Uneven Terrain
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
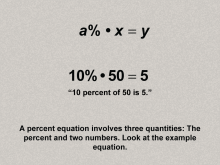
Math Clip Art--Ratios, Proportions, Percents--Percents 11 | Math Clip Art--Ratios, Proportions, Percents--Percents 11TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of the general equation for percents: a% * x = y, using the example 10% * 50 = 5. It emphasizes the three components of a percent equation: the percent, a base number, and the result, and expands on this idea by showing that establishes the foundational equation for solving percent problems, serving as a gateway to explore specific types of percent equations. |
Percents |
|
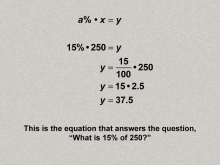
Math Clip Art--Ratios, Proportions, Percents--Percents 12 | Math Clip Art--Ratios, Proportions, Percents--Percents 12TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of how to solve the question 'what is 15% of 250?' using the equation a% * x = y, with calculations explicitly shown as 15 * 2.5 = 37.5. and expands on this idea by showing that provides a clear, step-by-step example to apply the general percent equation, enhancing comprehension through practical application. |
Percents |
|
Math Clip Art--Ratios, Proportions, Percents--Percents 13 | Math Clip Art--Ratios, Proportions, Percents--Percents 13TopicRatios, Proportions, and Percents DescriptionThe image illustrates the concept of solving '150 is 30% of what number?' using the same equation a% * x = y and algebraic manipulation to find x = 500 and expands on this idea by showing that explains how to rearrange the percent equation to solve for different variables, expanding on problem-solving strategies. |
Percents |
|
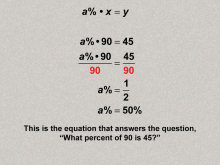
Math Clip Art--Ratios, Proportions, Percents--Percents 14 | Math Clip Art--Ratios, Proportions, Percents--Percents 14TopicRatios, Proportions, and Percents DescriptionThe image illustrates solving the problem 'what percent of 90 is 45?' using the equation a% * x = y, and algebraically finding a% = 50% and expands on this idea by showing that demonstrates how to find the percent in percent equations, further developing flexibility in solving percent-related problems. |
Percents |
|
Math Clip Art--Ratios, Proportions, Percents--Percents 15 | Math Clip Art--Ratios, Proportions, Percents--Percents 15TopicRatios, Proportions, and Percents DescriptionThe image summarizes the three types of percent equations in a table format, highlighting the unknown variable in each scenario (percent, part, or whole) and expands on this idea by providing a comprehensive overview and categorization of percent problems, solidifying the framework introduced in earlier examples. |
Percents |
|
Math Clip Art--Ratios, Proportions, Percents--Proportions 01 | Math Clip Art--Ratios, Proportions, Percents--Proportions 01TopicRatios, Proportions, and Percents DescriptionThis image showcases the concept of proportions using a dynamic visual of a runner in action framed within a golden ratio spiral. The proportion is represented algebraically as a/b = c/d, linking visual and mathematical representations. It introduces proportions conceptually and visually, setting the foundation for the subsequent examples. |
Proportions |
|
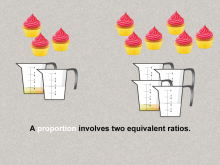
Math Clip Art--Ratios, Proportions, Percents--Proportions 02 | Math Clip Art--Ratios, Proportions, Percents--Proportions 02TopicRatios, Proportions, and Percents DescriptionThis image illustrates proportions using two equivalent ratios, represented by measuring cups and cupcakes. It simplifies proportions to relatable everyday examples. It connects proportions to practical examples, emphasizing the real-world relevance. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Proportions 03 | Math Clip Art--Ratios, Proportions, Percents--Proportions 03TopicRatios, Proportions, and Percents DescriptionThis image uses coins to demonstrate proportions. The image compares groups of quarters and nickels to highlight equivalent ratios (3:1 and 6:2). It solidifies the concept of equivalent ratios through another real-life example, reinforcing the idea. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Proportions 04 | Math Clip Art--Ratios, Proportions, Percents--Proportions 04TopicRatios, Proportions, and Percents DescriptionThis image demonstrates proportions through a scale model example, comparing the height and width ratios of the Eiffel Tower in two scales. It highlights the application of proportions in scaling and models, bridging abstract and practical understanding. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
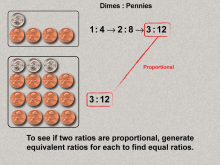
Math Clip Art--Ratios, Proportions, Percents--Proportions 05 | Math Clip Art--Ratios, Proportions, Percents--Proportions 05TopicRatios, Proportions, and Percents DescriptionThis image shows proportionality between dimes and pennies using equivalent ratios (1:4 and 3:12). Mathematical steps verify proportionality. It introduces proportional reasoning and calculation steps to ensure clarity in identifying proportional relationships. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
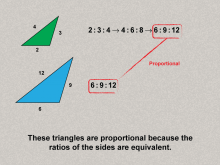
Math Clip Art--Ratios, Proportions, Percents--Proportions 06 | Math Clip Art--Ratios, Proportions, Percents--Proportions 06TopicRatios, Proportions, and Percents DescriptionThis image presents proportional triangles, with side lengths maintaining equivalent ratios (2:3:4 and 6:9:12). It demonstrates geometric applications of proportions, extending the concept to shapes and measurements. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Proportions 07 | Math Clip Art--Ratios, Proportions, Percents--Proportions 07TopicRatios, Proportions, and Percents DescriptionThis image contrasts proportionality with non-proportional groups of coins (dimes and nickels). Ratios differ, clarifying when proportions do not exist. It explains non-proportionality to deepen understanding of proportional relationships. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
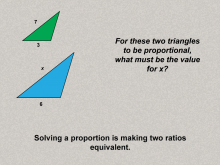
Math Clip Art--Ratios, Proportions, Percents--Proportions 08 | Math Clip Art--Ratios, Proportions, Percents--Proportions 08TopicRatios, Proportions, and Percents DescriptionThis image poses a question about proportional triangles, asking for the missing value (x) to maintain proportionality. It introduces problem-solving involving proportions, encouraging engagement and application. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
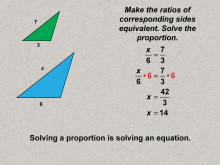
Math Clip Art--Ratios, Proportions, Percents--Proportions 09 | Math Clip Art--Ratios, Proportions, Percents--Proportions 09TopicRatios, Proportions, and Percents DescriptionThis image solves the posed proportion problem by finding the value of x using equivalent ratios (x/6 = 7/3). It breaks down the process of solving proportions, reinforcing mathematical reasoning. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Proportions 10 | Math Clip Art--Ratios, Proportions, Percents--Proportions 10TopicRatios, Proportions, and Percents DescriptionThis image demonstrates proportionality in coins by calculating the number of nickels required for proportional groups (2/5 = 6/x). It closes the sequence with a real-world problem, consolidating the topic and providing a practical application. Proportions are a foundational concept in mathematics, connecting ratios to real-world applications. Examples like those in this collection help students visualize and reason about proportional relationships in meaningful contexts, solidifying their understanding. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 01
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 02
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
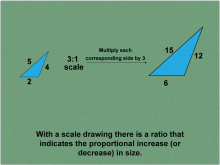
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 03
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
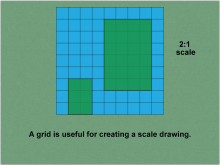
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 04
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 05
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06 | Math Clip Art--Ratios, Proportions, Percents--Scale Drawings and Scale Models 06
This is part of a collection of math clip art images that explain different aspects of ratios, proportions, and percents. |
Proportions |
|
Math Example--Math of Money--Calculating Tax--Example 1 | Math Example--Math of Money--Calculating Tax--Example 1TopicThe Math of Money DescriptionWhat is the tax due on a $1000 purchase when the sales tax rate is 5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |
|
Math Example--Math of Money--Calculating Tax--Example 10 | Math Example--Math of Money--Calculating Tax--Example 10TopicThe Math of Money DescriptionWhat is the tax due on a $9999.99 purchase when the sales tax rate is 9.9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |
|
Math Example--Math of Money--Calculating Tax--Example 2 | Math Example--Math of Money--Calculating Tax--Example 2TopicThe Math of Money DescriptionWhat is the tax due on a $1500 purchase when the sales tax rate is 6%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |
|
Math Example--Math of Money--Calculating Tax--Example 3 | Math Example--Math of Money--Calculating Tax--Example 3TopicThe Math of Money DescriptionWhat is the tax due on a $2550 purchase when the sales tax rate is 7%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |
|
Math Example--Math of Money--Calculating Tax--Example 4 | Math Example--Math of Money--Calculating Tax--Example 4TopicThe Math of Money DescriptionWhat is the tax due on a $999 purchase when the sales tax rate is 8%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |
|
Math Example--Math of Money--Calculating Tax--Example 5 | Math Example--Math of Money--Calculating Tax--Example 5TopicThe Math of Money DescriptionWhat is the tax due on a $999.99 purchase when the sales tax rate is 9%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |
|
Math Example--Math of Money--Calculating Tax--Example 6 | Math Example--Math of Money--Calculating Tax--Example 6TopicThe Math of Money DescriptionWhat is the tax due on a $1250 purchase when the sales tax rate is 6.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |
|
Math Example--Math of Money--Calculating Tax--Example 7 | Math Example--Math of Money--Calculating Tax--Example 7TopicThe Math of Money DescriptionWhat is the tax due on a $1399 purchase when the sales tax rate is 7.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |
|
Math Example--Math of Money--Calculating Tax--Example 8 | Math Example--Math of Money--Calculating Tax--Example 8TopicThe Math of Money DescriptionWhat is the tax due on a $1575.50 purchase when the sales tax rate is 8.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |
|
Math Example--Math of Money--Calculating Tax--Example 9 | Math Example--Math of Money--Calculating Tax--Example 9TopicThe Math of Money DescriptionWhat is the tax due on a $1999.99 purchase when the sales tax rate is 9.5%? The example shows how to apply the formula Tax Due = Cost * Tax Rate. Calculating tax is a fundamental skill in understanding financial literacy. This example and others like it help illustrate how percentages are applied in real-world scenarios, such as shopping and services. Seeing multiple worked-out examples allows students to recognize patterns and reinforce their understanding of applying formulas consistently in various contexts. It ensures they can adapt to different numbers and situations. |
Percents |
|
Math Example--Math of Money--Calculating Tips and Commissions--Example 1 | Math Example--Math of Money--Calculating Tips and Commissions--Example 1TopicThe Math of Money DescriptionCalculate a 15% tip on a $50 restaurant bill. The problem requires finding 15% of 50. To calculate the tip, multiply the cost (50) by the tip rate (0.15). Tip = 50 * 0.15 = 7.50. The answer is $7.50. In general, the topic 'The Math of Money' covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |
|
Math Example--Math of Money--Calculating Tips and Commissions--Example 10 | Math Example--Math of Money--Calculating Tips and Commissions--Example 10TopicThe Math of Money DescriptionCalculate a 9.5% sales commission on a $350,999 sale. The problem requires finding 9.5% of 350,999. To calculate the commission, multiply the sale amount (350,999) by the commission rate (0.095). Commission = 350,999 * 0.095 ≈ 33,344.91. The answer is approximately $33,344.91. |
Percents |
|
Math Example--Math of Money--Calculating Tips and Commissions--Example 2 | Math Example--Math of Money--Calculating Tips and Commissions--Example 2TopicThe Math of Money DescriptionCalculate a 16% tip on a $55 restaurant bill. The problem requires finding 16% of 55. To calculate the tip, multiply the cost (55) by the tip rate (0.16). Tip = 55 * 0.16 = 8.8. The answer is $8.80. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |
|
Math Example--Math of Money--Calculating Tips and Commissions--Example 3 | Math Example--Math of Money--Calculating Tips and Commissions--Example 3TopicThe Math of Money DescriptionCalculate an 18% tip on a $75.50 restaurant bill. The problem requires finding 18% of 75.50. To calculate the tip, multiply the cost (75.50) by the tip rate (0.18). Tip = 75.50 * 0.18 = 13.59. The answer is $13.59. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |
|
Math Example--Math of Money--Calculating Tips and Commissions--Example 4 | Math Example--Math of Money--Calculating Tips and Commissions--Example 4TopicThe Math of Money DescriptionCalculate a 19.5% tip on a $49.99 restaurant bill. The problem requires finding 19.5% of 49.99. To calculate the tip, multiply the cost (49.99) by the tip rate (0.195). Tip = 49.99 * 0.195 Å 9.75. The answer is approximately $9.75. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |
|
Math Example--Math of Money--Calculating Tips and Commissions--Example 5 | Math Example--Math of Money--Calculating Tips and Commissions--Example 5TopicThe Math of Money DescriptionCalculate a 22.5% tip on a $159.99 restaurant bill. The problem requires finding 22.5% of 159.99. To calculate the tip, multiply the cost (159.99) by the tip rate (0.225). Tip = 159.99 * 0.225 ≈ 35.99. The answer is approximately $35.99. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |
|
Math Example--Math of Money--Calculating Tips and Commissions--Example 6 | Math Example--Math of Money--Calculating Tips and Commissions--Example 6TopicThe Math of Money DescriptionCalculate a 5% sales commission on a $1000 sale. The problem requires finding 5% of 1000. To calculate the commission, multiply the sale amount (1000) by the commission rate (0.05). Commission = 1000 * 0.05 = 50. The answer is $50. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |
|
Math Example--Math of Money--Calculating Tips and Commissions--Example 7 | Math Example--Math of Money--Calculating Tips and Commissions--Example 7TopicThe Math of Money DescriptionCalculate a 6% sales commission on a $1200 sale. The problem requires finding 6% of 1200. To calculate the commission, multiply the sale amount (1200) by the commission rate (0.06). Commission = 1200 * 0.06 = 72. The answer is $72. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |
|
Math Example--Math of Money--Calculating Tips and Commissions--Example 8 | Math Example--Math of Money--Calculating Tips and Commissions--Example 8TopicThe Math of Money DescriptionCalculate a 7.5% sales commission on a $25,500 sale. The problem requires finding 7.5% of 25,500. To calculate the commission, multiply the sale amount (25,500) by the commission rate (0.075). Commission = 25,500 * 0.075 = 1912.50. The answer is $1,912.50. In general, the topic "The Math of Money" covers understanding the calculation of financial metrics like tips and commissions. Examples in this collection focus on real-world scenarios where these calculations are necessary, helping students grasp the mathematical principles involved. |
Percents |
|
Math Example--Math of Money--Calculating Tips and Commissions--Example 9 | Math Example--Math of Money--Calculating Tips and Commissions--Example 9TopicThe Math of Money DescriptionCalculate an 8.5% sales commission on a $125,500 sale. The problem requires finding 8.5% of 125,500. To calculate the commission, multiply the sale amount (125,500) by the commission rate (0.085). Commission = 125,500 * 0.085 = 10,667.50. The answer is $10,667.50. |
Percents |
|
Math Example--Math of Money--Compound Interest: Example 1 | Math Example--Math of Money--Compound Interest: Example 1TopicMath of Money DescriptionThis example demonstrates compound interest calculation for a $1000 investment at a 2.5% interest rate over 5 years, compounded annually. Using the formula A = P(1 + r/n)nt, where P is the principal amount, r is the interest rate, n is the number of times interest is compounded per year, and t is the number of years, the final amount is calculated to be $1131.41. |
Compound Interest |
|
Math Example--Math of Money--Compound Interest: Example 10 | Math Example--Math of Money--Compound Interest: Example 10TopicMath of Money DescriptionThis example calculates compound interest for a $1000 investment at a 5% interest rate over 5 years, compounded monthly. Using the formula A = P(1 + r/n)nt, where P = 1000, r = 0.05, n = 12, and t = 5, the final amount is $1283.61. Compound interest is a key concept in financial mathematics that shows how investments grow over time. This example highlights monthly compounding, demonstrating the impact of more frequent compounding on returns. Understanding these differences helps students apply compound interest in real-world financial scenarios. |
Compound Interest |
|
Math Example--Math of Money--Compound Interest: Example 11 | Math Example--Math of Money--Compound Interest: Example 11TopicMath of Money DescriptionThis example calculates compound interest for a $1000 investment at a 5% interest rate over 5 years, compounded daily. The formula $$A = P(1 + r/n)nt is used with P = 1000, r = 0.05, n = 365, and t = 5, resulting in an amount of $1284.00. Understanding compound interest is crucial for financial literacy. This example demonstrates daily compounding and its effect on investment growth compared to other frequencies. By exploring various scenarios, students learn how different compounding intervals influence financial outcomes. |
Compound Interest |
|
Math Example--Math of Money--Compound Interest: Example 12 | Math Example--Math of Money--Compound Interest: Example 12TopicMath of Money DescriptionThis example calculates compound interest for a $1000 investment at a 5% interest rate over 5 years, compounded continuously. Using the formula A = Pert, where P = 1000, r = 0.05, and t = 5, the final amount is $1284.03. Compound interest is a fundamental concept in finance, illustrating how investments grow exponentially over time. This example highlights continuous compounding, which shows the impact of applying interest at every possible moment. Understanding these differences helps students apply compound interest in real-world financial scenarios. |
Compound Interest |
|
Math Example--Math of Money--Compound Interest: Example 13 | Math Example--Math of Money--Compound Interest: Example 13TopicMath of Money DescriptionThis example calculates compound interest for a $1000 investment with an interest rate of 2.5% over 10 years, compounded annually. Using the formula A = P(1 + r/n)nt, where P = 1000, r = 0.025, n = 1, and $$t = 10, the final amount is $1280.08. Understanding compound interest is crucial for financial literacy. This example demonstrates annual compounding and its effect on investment growth compared to other frequencies. By exploring various scenarios, students learn how different compounding intervals influence financial outcomes. |
Compound Interest |
|
Math Example--Math of Money--Compound Interest: Example 14 | Math Example--Math of Money--Compound Interest: Example 14TopicMath of Money DescriptionThis example calculates compound interest for a $1000 investment with a 2.5% interest rate, compounded semi-annually over 10 years. Using the formula A = P(1 + r/n)nt, where P = 1000, r = 0.025, n = 2, and t = 10, the final amount is $1282.04. Understanding compound interest is essential for financial literacy. This example demonstrates semi-annual compounding and its effect on investment growth compared to other frequencies. By exploring various scenarios, students learn how different compounding intervals influence financial outcomes. |
Compound Interest |
|
Math Example--Math of Money--Compound Interest: Example 15 | Math Example--Math of Money--Compound Interest: Example 15TopicMath of Money DescriptionThis example calculates compound interest for a $1000 investment with a 2.5% interest rate, compounded quarterly over 10 years. Using the formula A = P(1 + r/n)nt, where P = 1000, r = 0.025, n = 4, and t = 10, the final amount is $1283.03. Understanding compound interest is crucial for financial literacy. This example demonstrates quarterly compounding and its effect on investment growth compared to other frequencies. By exploring various scenarios, students learn how different compounding intervals influence financial outcomes. |
Compound Interest |
|
Math Example--Math of Money--Compound Interest: Example 16 | Math Example--Math of Money--Compound Interest: Example 16TopicMath of Money DescriptionThis example calculates compound interest for a $1000 investment with a 2.5% interest rate, compounded monthly over 10 years. Using the formula A = P(1 + r/n)nt, where P = 1000, r = 0.025, n = 12, and t = 10, the final amount is $1283.18. Understanding compound interest is crucial for financial literacy. This example demonstrates monthly compounding and its effect on investment growth compared to other frequencies. By exploring various scenarios, students learn how different compounding intervals influence financial outcomes. |
Compound Interest |
|
Math Example--Math of Money--Compound Interest: Example 17 | Math Example--Math of Money--Compound Interest: Example 17TopicMath of Money DescriptionThis example demonstrates compound interest calculation for a $1000 investment at a 2.5% interest rate over 10 years, compounded daily. Using the formula A = P(1 + r/n)nt, with P = 1000, r = 0.025, n = 365, and t = 10, the result is $1284.01. Understanding compound interest is essential for financial literacy. This example demonstrates daily compounding and its effect on investment growth compared to other frequencies. By exploring various scenarios, students learn how different compounding intervals influence financial outcomes. |
Compound Interest |
