
Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 4: Restaurant Floor Plan
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
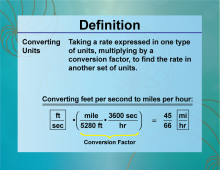
Definition--Ratios, Proportions, and Percents Concepts--Converting Units | Converting UnitsTopicRatios, Proportions, and Percents DefinitionConverting units involves changing a measurement from one unit to another using a conversion factor. DescriptionConverting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Converting Units | Converting UnitsTopicRatios, Proportions, and Percents DefinitionConverting units involves changing a measurement from one unit to another using a conversion factor. DescriptionConverting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Converting Units | Converting UnitsTopicRatios, Proportions, and Percents DefinitionConverting units involves changing a measurement from one unit to another using a conversion factor. DescriptionConverting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Converting Units | Converting UnitsTopicRatios, Proportions, and Percents DefinitionConverting units involves changing a measurement from one unit to another using a conversion factor. DescriptionConverting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis | Dimensional AnalysisTopicRatios, Proportions, and Percents DefinitionDimensional analysis is a method used to convert one unit of measurement to another using conversion factors. DescriptionDimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds: |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis | Dimensional AnalysisTopicRatios, Proportions, and Percents DefinitionDimensional analysis is a method used to convert one unit of measurement to another using conversion factors. DescriptionDimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds: |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis | Dimensional AnalysisTopicRatios, Proportions, and Percents DefinitionDimensional analysis is a method used to convert one unit of measurement to another using conversion factors. DescriptionDimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds: |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis | Dimensional AnalysisTopicRatios, Proportions, and Percents DefinitionDimensional analysis is a method used to convert one unit of measurement to another using conversion factors. DescriptionDimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds: |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis | Dimensional AnalysisTopicRatios, Proportions, and Percents DefinitionDimensional analysis is a method used to convert one unit of measurement to another using conversion factors. DescriptionDimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds: |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Dimensional Analysis | Dimensional AnalysisTopicRatios, Proportions, and Percents DefinitionDimensional analysis is a method used to convert one unit of measurement to another using conversion factors. DescriptionDimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit. For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors 1 meter = 0.001 kilometers and 1 hour = 3600 seconds: |
Applications of Ratios, Proportions, and Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios | Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios | Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios | Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios | Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios | Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios | Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios | Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios | Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios | Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios | Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios | Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios | Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios | Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios | Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios | Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios | Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios | Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios | Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent | PercentTopicRatios, Proportions, and Percents DefinitionA percent is a ratio that compares a number to 100. DescriptionPercentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates. For example, if you score 45 out of 50 on a test, your percentage score is (45/50) × 100 = 90% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Decrease | Percent DecreaseTopicRatios, Proportions, and Percents DefinitionPercent decrease measures the reduction in value expressed as a percentage of the original value. DescriptionPercent decrease is used to quantify the reduction in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as price reductions and weight loss. For example, if the price of a jacket drops from $80 to $60, the percent decrease is calculated as (80 − 60)/80 × 100 = 25%. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Decrease | Percent DecreaseTopicRatios, Proportions, and Percents DefinitionPercent decrease measures the reduction in value expressed as a percentage of the original value. DescriptionPercent decrease is used to quantify the reduction in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as price reductions and weight loss. For example, if the price of a jacket drops from $80 to $60, the percent decrease is calculated as (80 − 60)/80 × 100 = 25%. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Decrease | Percent DecreaseTopicRatios, Proportions, and Percents DefinitionPercent decrease measures the reduction in value expressed as a percentage of the original value. DescriptionPercent decrease is used to quantify the reduction in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as price reductions and weight loss. For example, if the price of a jacket drops from $80 to $60, the percent decrease is calculated as (80 − 60)/80 × 100 = 25%. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Decrease | Percent DecreaseTopicRatios, Proportions, and Percents DefinitionPercent decrease measures the reduction in value expressed as a percentage of the original value. DescriptionPercent decrease is used to quantify the reduction in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as price reductions and weight loss. For example, if the price of a jacket drops from $80 to $60, the percent decrease is calculated as (80 − 60)/80 × 100 = 25%. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Decrease | Percent DecreaseTopicRatios, Proportions, and Percents DefinitionPercent decrease measures the reduction in value expressed as a percentage of the original value. DescriptionPercent decrease is used to quantify the reduction in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as price reductions and weight loss. For example, if the price of a jacket drops from $80 to $60, the percent decrease is calculated as (80 − 60)/80 × 100 = 25%. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Decrease | Percent DecreaseTopicRatios, Proportions, and Percents DefinitionPercent decrease measures the reduction in value expressed as a percentage of the original value. DescriptionPercent decrease is used to quantify the reduction in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as price reductions and weight loss. For example, if the price of a jacket drops from $80 to $60, the percent decrease is calculated as (80 − 60)/80 × 100 = 25%. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Increase | Percent IncreaseTopicRatios, Proportions, and Percents DefinitionPercent increase measures the growth in value expressed as a percentage of the original value. DescriptionPercent increase is used to quantify the growth in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as salary increases and population growth. For example, if the price of a stock rises from \$50 to \$75, the percent increase is calculated as (75 − 50)/50 × 100 = 50% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Increase | Percent IncreaseTopicRatios, Proportions, and Percents DefinitionPercent increase measures the growth in value expressed as a percentage of the original value. DescriptionPercent increase is used to quantify the growth in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as salary increases and population growth. For example, if the price of a stock rises from \$50 to \$75, the percent increase is calculated as (75 − 50)/50 × 100 = 50% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Increase | Percent IncreaseTopicRatios, Proportions, and Percents DefinitionPercent increase measures the growth in value expressed as a percentage of the original value. DescriptionPercent increase is used to quantify the growth in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as salary increases and population growth. For example, if the price of a stock rises from \$50 to \$75, the percent increase is calculated as (75 − 50)/50 × 100 = 50% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Increase | Percent IncreaseTopicRatios, Proportions, and Percents DefinitionPercent increase measures the growth in value expressed as a percentage of the original value. DescriptionPercent increase is used to quantify the growth in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as salary increases and population growth. For example, if the price of a stock rises from \$50 to \$75, the percent increase is calculated as (75 − 50)/50 × 100 = 50% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Increase | Percent IncreaseTopicRatios, Proportions, and Percents DefinitionPercent increase measures the growth in value expressed as a percentage of the original value. DescriptionPercent increase is used to quantify the growth in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as salary increases and population growth. For example, if the price of a stock rises from \$50 to \$75, the percent increase is calculated as (75 − 50)/50 × 100 = 50% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent Increase | Percent IncreaseTopicRatios, Proportions, and Percents DefinitionPercent increase measures the growth in value expressed as a percentage of the original value. DescriptionPercent increase is used to quantify the growth in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as salary increases and population growth. For example, if the price of a stock rises from \$50 to \$75, the percent increase is calculated as (75 − 50)/50 × 100 = 50% |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent of a Number | Percent of a NumberTopicRatios, Proportions, and Percents DefinitionPercent of a number involves calculating the amount represented by a certain percentage of that number. DescriptionUnderstanding percentages is crucial for working with finances, statistics, and data analysis. For instance, to find 20% of 50, multiply 50 by 0.20, resulting in 10. Likewise, it's important for everyday scenarios, such as calculating discounts during shopping. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent of a Number | Percent of a NumberTopicRatios, Proportions, and Percents DefinitionPercent of a number involves calculating the amount represented by a certain percentage of that number. DescriptionUnderstanding percentages is crucial for working with finances, statistics, and data analysis. For instance, to find 20% of 50, multiply 50 by 0.20, resulting in 10. Likewise, it's important for everyday scenarios, such as calculating discounts during shopping. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent of a Number | Percent of a NumberTopicRatios, Proportions, and Percents DefinitionPercent of a number involves calculating the amount represented by a certain percentage of that number. DescriptionUnderstanding percentages is crucial for working with finances, statistics, and data analysis. For instance, to find 20% of 50, multiply 50 by 0.20, resulting in 10. Likewise, it's important for everyday scenarios, such as calculating discounts during shopping. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent of a Number | Percent of a NumberTopicRatios, Proportions, and Percents DefinitionPercent of a number involves calculating the amount represented by a certain percentage of that number. DescriptionUnderstanding percentages is crucial for working with finances, statistics, and data analysis. For instance, to find 20% of 50, multiply 50 by 0.20, resulting in 10. Likewise, it's important for everyday scenarios, such as calculating discounts during shopping. |
Percents |