
Illustrative Math Alignment: Grade 7 Unit 9
Putting it All Together
Lesson 4: Restaurant Floor Plan
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Definition--Ratios, Proportions, and Percents Concepts--Percent of a Number | Percent of a NumberTopicRatios, Proportions, and Percents DefinitionPercent of a number involves calculating the amount represented by a certain percentage of that number. DescriptionUnderstanding percentages is crucial for working with finances, statistics, and data analysis. For instance, to find 20% of 50, multiply 50 by 0.20, resulting in 10. Likewise, it's important for everyday scenarios, such as calculating discounts during shopping. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent of a Number | Percent of a NumberTopicRatios, Proportions, and Percents DefinitionPercent of a number involves calculating the amount represented by a certain percentage of that number. DescriptionUnderstanding percentages is crucial for working with finances, statistics, and data analysis. For instance, to find 20% of 50, multiply 50 by 0.20, resulting in 10. Likewise, it's important for everyday scenarios, such as calculating discounts during shopping. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent of an Unknown | Percent of an UnknownTopicRatios, Proportions, and Percents DefinitionPercent of an unknown refers to solving for an unknown quantity when given a percentage of that quantity. DescriptionKnowing how to find a percentage of an unknown variable is essential for solving equations in algebra. This concept appears in various situations, such as when determining discounts or portions of a total amount. For instance, if 20% of an unknown number equals 15, you can set up the equation: 0.20x = 15 |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent of an Unknown | Percent of an UnknownTopicRatios, Proportions, and Percents DefinitionPercent of an unknown refers to solving for an unknown quantity when given a percentage of that quantity. DescriptionKnowing how to find a percentage of an unknown variable is essential for solving equations in algebra. This concept appears in various situations, such as when determining discounts or portions of a total amount. For instance, if 20% of an unknown number equals 15, you can set up the equation: 0.20x = 15 |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent of an Unknown | Percent of an UnknownTopicRatios, Proportions, and Percents DefinitionPercent of an unknown refers to solving for an unknown quantity when given a percentage of that quantity. DescriptionKnowing how to find a percentage of an unknown variable is essential for solving equations in algebra. This concept appears in various situations, such as when determining discounts or portions of a total amount. For instance, if 20% of an unknown number equals 15, you can set up the equation: 0.20x = 15 |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent of an Unknown | Percent of an UnknownTopicRatios, Proportions, and Percents DefinitionPercent of an unknown refers to solving for an unknown quantity when given a percentage of that quantity. DescriptionKnowing how to find a percentage of an unknown variable is essential for solving equations in algebra. This concept appears in various situations, such as when determining discounts or portions of a total amount. For instance, if 20% of an unknown number equals 15, you can set up the equation: 0.20x = 15 |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent of an Unknown | Percent of an UnknownTopicRatios, Proportions, and Percents DefinitionPercent of an unknown refers to solving for an unknown quantity when given a percentage of that quantity. DescriptionKnowing how to find a percentage of an unknown variable is essential for solving equations in algebra. This concept appears in various situations, such as when determining discounts or portions of a total amount. For instance, if 20% of an unknown number equals 15, you can set up the equation: 0.20x = 15 |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percent of an Unknown | Percent of an UnknownTopicRatios, Proportions, and Percents DefinitionPercent of an unknown refers to solving for an unknown quantity when given a percentage of that quantity. DescriptionKnowing how to find a percentage of an unknown variable is essential for solving equations in algebra. This concept appears in various situations, such as when determining discounts or portions of a total amount. For instance, if 20% of an unknown number equals 15, you can set up the equation: 0.20x = 15 |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percents as Decimals | Percents as DecimalsTopicRatios, Proportions, and Percents DefinitionPercents as decimals involve converting a percentage into its decimal representation. DescriptionConverting percents to decimals is a key skill in mathematics, allowing students to perform calculations involving percentages more easily. To convert, divide the percent by 100. For example, 75% as a decimal is 0.75, calculated by dividing 75 by 100. This conversion is useful in many contexts, such as finance, where calculations are conducted using decimal values. Mastering this concept enables students to approach real-world problems with greater confidence and accuracy. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percents as Decimals | Percents as DecimalsTopicRatios, Proportions, and Percents DefinitionPercents as decimals involve converting a percentage into its decimal representation. DescriptionConverting percents to decimals is a key skill in mathematics, allowing students to perform calculations involving percentages more easily. To convert, divide the percent by 100. For example, 75% as a decimal is 0.75, calculated by dividing 75 by 100. This conversion is useful in many contexts, such as finance, where calculations are conducted using decimal values. Mastering this concept enables students to approach real-world problems with greater confidence and accuracy. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percents as Decimals | Percents as DecimalsTopicRatios, Proportions, and Percents DefinitionPercents as decimals involve converting a percentage into its decimal representation. DescriptionConverting percents to decimals is a key skill in mathematics, allowing students to perform calculations involving percentages more easily. To convert, divide the percent by 100. For example, 75% as a decimal is 0.75, calculated by dividing 75 by 100. This conversion is useful in many contexts, such as finance, where calculations are conducted using decimal values. Mastering this concept enables students to approach real-world problems with greater confidence and accuracy. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percents as Decimals | Percents as DecimalsTopicRatios, Proportions, and Percents DefinitionPercents as decimals involve converting a percentage into its decimal representation. DescriptionConverting percents to decimals is a key skill in mathematics, allowing students to perform calculations involving percentages more easily. To convert, divide the percent by 100. For example, 75% as a decimal is 0.75, calculated by dividing 75 by 100. This conversion is useful in many contexts, such as finance, where calculations are conducted using decimal values. Mastering this concept enables students to approach real-world problems with greater confidence and accuracy. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percents as Decimals | Percents as DecimalsTopicRatios, Proportions, and Percents DefinitionPercents as decimals involve converting a percentage into its decimal representation. DescriptionConverting percents to decimals is a key skill in mathematics, allowing students to perform calculations involving percentages more easily. To convert, divide the percent by 100. For example, 75% as a decimal is 0.75, calculated by dividing 75 by 100. This conversion is useful in many contexts, such as finance, where calculations are conducted using decimal values. Mastering this concept enables students to approach real-world problems with greater confidence and accuracy. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Percents as Decimals | Percents as DecimalsTopicRatios, Proportions, and Percents DefinitionPercents as decimals involve converting a percentage into its decimal representation. DescriptionConverting percents to decimals is a key skill in mathematics, allowing students to perform calculations involving percentages more easily. To convert, divide the percent by 100. For example, 75% as a decimal is 0.75, calculated by dividing 75 by 100. This conversion is useful in many contexts, such as finance, where calculations are conducted using decimal values. Mastering this concept enables students to approach real-world problems with greater confidence and accuracy. |
Percents |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportion | ProportionTopicRatios, Proportions, and Percents DefinitionA proportion is an equation that states that two ratios are equal. DescriptionUnderstanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models. To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Proportional | ProportionalTopicRatios, Proportions, and Percents DefinitionProportional refers to the relationship between two quantities where their ratio is constant. DescriptionProportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering. For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations. |
Proportions |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate | RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio | RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions | Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |
|
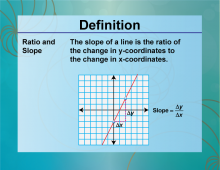
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope | Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |