Illustrative Math Alignment: Grade 7 Unit 9

In this video learn the mechanics of solving one-step equations involving addition. .

In this video learn the mechanics of solving one-step equations involving addition. .

In this video learn the mechanics of solving one-step equations involving division. .

In this video learn the mechanics of solving one-step equations involving multiplication. .

In this video learn the mechanics of solving one-step equations involving subtraction. .

In this video learn the mechanics of solving one-step equations involving subtraction. .

Video Tutorial: Integers: Variable Expressions with Integers. In this video, students simplify various variable expressions that use integers. A

This is part of a series of videos on the topic of Integers. This includes defining integers, modeling integers, integer operations, and integer expressions.

The following section includes background information on integers (and also rational numbers). Refer to this section as you view the videos, or as review material afterward.

Video Tutorial: One-Step Equations: Addition. In this video, get an overview of one-step equations and how to solve them. In particular, look at one-step addition equations.

Video Tutorial: One-Step Equations: Division. In this video, students get an overview of one-step equations and how to solve them. In particular, look at one-step division equations.

Video Tutorial: One-Step Equations: Multiplication. In this video, students get an overview of one-step equations and how to solve them. In particular, look at one-step multiplication equations.

Video Tutorial: One-Step Equations: Subtraction. In this video, students get an overview of one-step equations and how to solve them. In particular, look at one-step subtraction equations.

This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers.

The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.

What Are Ratios?

A ratio is the relationship between two or more quantities among a group of items.

Video Tutorial: Two-Step Equations: Division and Addition. In this video, we will solve a two-step equation that involves division and addition.

Video Tutorial: Two-Step Equations: Division and Subtraction. In this video, we will solve a two-step equation that involves division and subtraction.

Video Tutorial: Two-Step Equations: Multiplication and Addition. In this video, we will solve a two-step equation that involves multiplication and addition.

Video Tutorial: Two-Step Equations: Multiplication and Subtraction. In this video, we will solve a two-step equation that involves multiplication and subtraction.

Topic

Ratios, Proportions, and Percents

Definition

Calculating tax involves determining the percentage amount to be added to the base price of a product or service.

Description

Calculating tax is a fundamental application of percentages in real-world scenarios. When purchasing goods or services, the total cost is often the sum of the base price and the tax applied. Understanding how to calculate tax is essential for budgeting and financial literacy.

For example, if a product costs $50 and the tax rate is 8%, the tax amount is calculated as 

50 × 0.08 = 4

Therefore, the total cost is 

Topic

Ratios, Proportions, and Percents

Definition

Calculating tips involves determining the amount of money to give as a gratuity based on a percentage of the total bill.

Description

Calculating tips is a common use of percentages in everyday life, particularly in service industries such as dining. Tips are usually calculated as a percentage of the total bill, and understanding how to compute this is important for both customers and service providers. 

For instance, if a meal costs $80 and you want to leave a 15% tip, the tip amount is calculated as 

80 × 0.15 = 12

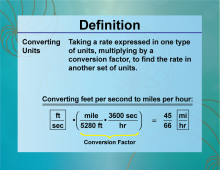
Topic

Ratios, Proportions, and Percents

Definition

Converting units involves changing a measurement from one unit to another using a conversion factor.

Description

Converting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters.

For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 

5 × 1.60934 = 8.0467 kilometers

Topic

Ratios, Proportions, and Percents

Definition

Dimensional analysis is a method used to convert one unit of measurement to another using conversion factors.

Description

Dimensional analysis is a powerful tool in mathematics and science for converting units and solving problems involving measurements. It uses the principle of multiplying by conversion factors to ensure that units cancel out appropriately, leading to the desired unit.

For example, to convert 50 meters per second to kilometers per hour, you use the conversion factors  1 meter = 0.001 kilometers and 1 hour = 3600 seconds: 

Topic

Ratios, Proportions, and Percents

Definition

Equivalent ratios are ratios that express the same relationship between quantities.

Description

Equivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models.

For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced.

Topic

Ratios, Proportions, and Percents

Definition

Part-to-part ratios compare different parts of a whole to each other.

Description

Part-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics.

For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3.

Topic

Ratios, Proportions, and Percents

Definition

Part-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions.

Description

Part-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making.

Topic

Ratios, Proportions, and Percents

Definition

A percent is a ratio that compares a number to 100.

Description

Percentages are a fundamental concept in mathematics, representing a ratio out of 100. They are used in various applications, including finance, statistics, and everyday calculations such as discounts and interest rates.

For example, if you score 45 out of 50 on a test, your percentage score is 

(45/50) × 100 = 90%

Topic

Ratios, Proportions, and Percents

Definition

Percent decrease measures the reduction in value expressed as a percentage of the original value.

Description

Percent decrease is used to quantify the reduction in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as price reductions and weight loss.

For example, if the price of a jacket drops from $80 to $60, the percent decrease is calculated as 

(80 − 60)/80 × 100 = 25%.

Topic

Ratios, Proportions, and Percents

Definition

Percent increase measures the growth in value expressed as a percentage of the original value.

Description

Percent increase is used to quantify the growth in value over time, expressed as a percentage of the original value. It is commonly used in finance, economics, and everyday scenarios such as salary increases and population growth.

For example, if the price of a stock rises from \$50 to \$75, the percent increase is calculated as 

(75 − 50)/50 × 100 = 50%

Topic

Ratios, Proportions, and Percents

Definition

Percent of a number involves calculating the amount represented by a certain percentage of that number.

Description

Understanding percentages is crucial for working with finances, statistics, and data analysis. For instance, to find 20% of 50, multiply 50 by 0.20, resulting in 10. Likewise, it's important for everyday scenarios, such as calculating discounts during shopping.

Topic

Ratios, Proportions, and Percents

Definition

Percent of an unknown refers to solving for an unknown quantity when given a percentage of that quantity.

Description

Knowing how to find a percentage of an unknown variable is essential for solving equations in algebra. This concept appears in various situations, such as when determining discounts or portions of a total amount.

For instance, if 20% of an unknown number equals 15, you can set up the equation: 

0.20x = 15

Topic

Ratios, Proportions, and Percents

Definition

Percents as decimals involve converting a percentage into its decimal representation.

Description

Converting percents to decimals is a key skill in mathematics, allowing students to perform calculations involving percentages more easily. To convert, divide the percent by 100.

For example, 75% as a decimal is 0.75, calculated by dividing 75 by 100. This conversion is useful in many contexts, such as finance, where calculations are conducted using decimal values. Mastering this concept enables students to approach real-world problems with greater confidence and accuracy.

Topic

Ratios, Proportions, and Percents

Definition

A proportion is an equation that states that two ratios are equal.

Description

Understanding proportions is essential in mathematics, as it is used to solve problems involving ratios and fractions. Proportions are commonly seen in real-world applications such as cooking, map measurements, and scale models.

To illustrate, if there are 2 apples for every 3 oranges, the proportion can be expressed as 2:3. Solving proportions involves finding and solving an equivalent ratio.

Topic

Ratios, Proportions, and Percents

Definition

Proportional refers to the relationship between two quantities where their ratio is constant.

Description

Proportional relationships are fundamental in mathematics and science, describing how one quantity changes in relation to another. This concept is used in various fields, including physics, economics, and engineering.

For example, if the speed of a car is proportional to the time it travels, doubling the time will double the distance covered. Understanding proportionality helps students solve complex problems and apply mathematical reasoning in real-world situations.

Topic

Ratios, Proportions, and Percents

Definition

A rate is a ratio that compares two quantities with different units.

Description

Rates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting.

For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems.

Topic

Ratios, Proportions, and Percents

Definition

A ratio is a comparison of two quantities by division.

Description

Ratios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance.

For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations.

Topic

Ratios, Proportions, and Percents

Definition

Ratios and fractions are both ways of comparing quantities, with fractions representing a part of a whole.

Description

Understanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio.

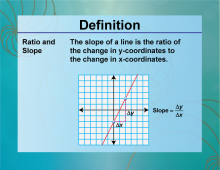
Topic

Ratios, Proportions, and Percents

Definition

The slope of a line is a ratio that represents the change in y over the change in x.

Description

Understanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points.

For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields.

Topic

Ratios, Proportions, and Percents

Definition

Ratios in simplest form are ratios that have been reduced to their smallest whole number terms.

Description

Reducing ratios to their simplest form is similar to the process of simplifying fractions, making it easier to compare and interpret data. A ratio is in simplest form when the greatest common divisor of the terms is 1.

For example, the ratio 8:12 simplifies to 2:3 by dividing both terms by their greatest common divisor, 4. This skill is essential for solving problems involving proportions and understanding relationships between quantities.

Topic

Ratios, Proportions, and Percents

Definition

Ratios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers.

Description

Ratios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons.

Topic

Ratios, Proportions, and Percents

Definition

Ratios with fractions compare two quantities where one or both of the quantities are fractions.

Description

Ratios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4.

Topic

Ratios, Proportions, and Percents

Definition

Ratios with percents involve comparing quantities where one or both of the quantities are expressed as percentages.

Description

Ratios with percents are widely used in various fields, including finance, statistics, and everyday life. For example, when comparing interest rates, growth rates, or discount rates, percentages are often used. Understanding these ratios allows for better financial decision-making and data analysis.

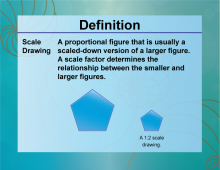
Topic

Ratios, Proportions, and Percents

Definition

A scale drawing is a representation of an object or structure with dimensions proportional to the actual object or structure.

Description

Scale drawings are essential in fields like architecture, engineering, and cartography, where accurate representations of large objects or areas are needed. For example, an architect might create a scale drawing of a building where 1 inch on the drawing represents 10 feet in reality. This allows for detailed planning and visualization without needing a full-sized model.

Topic

Ratios, Proportions, and Percents

Definition

A scale factor is a number that scales, or multiplies, some quantity.

Description

Scale factors are used in various applications, such as resizing images, models, and maps. For instance, if a model car is built at a scale factor of 1:24, it means the model is 1/24th the size of the actual car. This concept is crucial in fields requiring accurate scaling, such as architecture and engineering.

Topic

Ratios, Proportions, and Percents

Definition

Similar figures are figures that have the same shape but may differ in size; their corresponding angles are equal, and their corresponding sides are proportional.

Description

Similar figures are fundamental in geometry and are used in various real-world applications, such as creating scale models and maps. For example, two triangles are similar if their corresponding angles are equal and their sides are in proportion. This concept is essential for understanding geometric relationships and solving problems involving shapes and sizes.

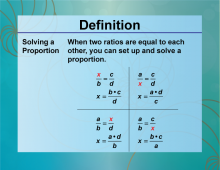
Topic

Ratios, Proportions, and Percents

Definition

Solving proportions involves finding the value of a variable that makes two ratios equal.

Description

Solving proportions is a key skill in algebra and is used in various applications, such as scaling recipes, converting units, and solving real-world problems. For example, if you know that 

2/3 = x/6

you can solve for x by cross-multiplying to get 

2 * 6 = 3 * x

leading to 

x = 4

Topic

Ratios, Proportions, and Percents

Definition

The constant of proportionality is the constant value that relates two proportional quantities.

Description

The constant of proportionality is a fundamental concept in mathematics, particularly in linear relationships and direct variation. For example, in the equation y = kx, k is the constant of proportionality that relates y and x. This concept is crucial in fields like physics, where it is used to describe relationships such as speed (distance/time).

Topic

Ratios, Proportions, and Percents

Definition

The Golden Ratio is a special number approximately equal to 1.618, often denoted by the Greek letter φ (phi), which appears in various aspects of art, architecture, and nature.

Topic

Ratios, Proportions, and Percents

Definition

The percent one number is of another is a way to express one number as a percentage of another number.

Description

Understanding how to express one number as a percentage of another is crucial in various real-world applications, such as calculating discounts, tax, and interest rates. For example, if you want to find out what percentage 25 is of 200, you divide 25 by 200 and multiply by 100, resulting in 12.5%.

Topic

Ratios, Proportions, and Percents

Definition

A unit rate is a comparison of any two separate but related measurements when one of the measurements is reduced to a single unit.

Description

Unit rates are commonly used in everyday life, such as calculating speed (miles per hour), cost per item, or efficiency (miles per gallon). For example, if a car travels 300 miles on 10 gallons of gas, the unit rate is 30 miles per gallon.

Topic

Ratios, Proportions, and Percents

Definition

Visual models for percents are diagrams or illustrations that represent percentages to help visualize and understand them.

Description

Visual models for percents are useful tools in various fields, such as education, finance, and statistics, to represent data and make it more comprehensible. For example, pie charts and bar graphs are common visual models that help illustrate percentages and proportions effectively.

Topic

Ratios, Proportions, and Percents

Definition

Visualizing equivalent ratios involves using diagrams or models to show that two ratios are equivalent.

Description

Visualizing equivalent ratios is important in fields such as mathematics and engineering, where understanding proportional relationships is crucial. For example, using a double number line or a ratio table can help illustrate that the ratios 2:3 and 4:6 are equivalent.