
Illustrative Math Alignment: Grade 8 Unit 1
Rigid Transformations and Congruence
Lesson 15: Adding the Angles in a Triangle
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8TopicGeometric Shapes DescriptionDetermine if two shapes on a grid are congruent. The shapes appear as two congruent triangles within a diamond shape, with each triangle reflected across the center axis. Using the grid, you can see that corresonding sides are congruent. Therefore, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. The triangles have differing shapes and orientations on the grid, suggesting different side lengths or angles. Therefore, they are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
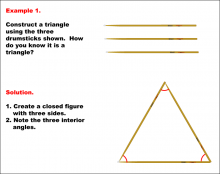
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 1 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 1TopicGeometry DescriptionThis image shows three drumsticks arranged to form a triangle. The drumsticks are placed in a closed triangular shape, with three angles marked in red. This example shows how to construct a triangle using drumsticks. The solution explains that to know it's a triangle, you need to create a closed figure with three sides and note the three interior angles. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
|
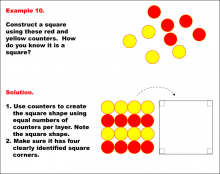
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 10 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 10TopicGeometry DescriptionThe image shows red and yellow circular counters arranged in a grid pattern to form a square shape. The solution explains how to arrange the counters in equal numbers per layer to form a square with four clearly defined corners. This example showcases how to construct a square using these red and yellow counters. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 2 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 2TopicGeometry DescriptionThis image shows a triangle drawn using a crayon. The triangle is closed with three sides, and the three angles are highlighted in red. This example showcases how to draw a triangle using a crayon or pencil. The solution states that to confirm it's a triangle, you need to create a closed figure with three sides and ensure it has three clearly identified angles. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
|
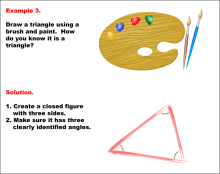
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 3 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 3TopicGeometry DescriptionThis image shows a triangle drawn using paint and a brush. The triangle is closed with three sides, and the three angles are marked in red. This example showcases how to draw a triangle using paint and a brush. The solution explains that to verify it's a triangle, you must create a closed figure with three sides and make sure it has three clearly identified angles. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 4 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 4TopicGeometry DescriptionThis image shows a triangle formed by arranging stickers in a triangular shape. The stickers form the sides of the triangle, and the angles are highlighted. This example showcases how to draw a triangle using stickers. The solution mentions that you can use stickers to form a closed figure with three sides, ensuring it has three clearly identified angles to confirm it's a triangle. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
|
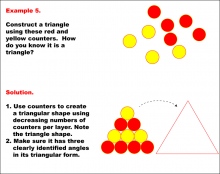
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 5 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 5TopicGeometry |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 6 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 6TopicGeometry DescriptionThe image features four drumsticks arranged in a square shape. The solution highlights how to verify that the figure is a square by checking that it has four sides and four square corners. This example showcases how to construct a square using four drumsticks. The text describes how to create a closed figure with four sides and check for square corners to confirm it's a square. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 7 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 7TopicGeometry |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
|
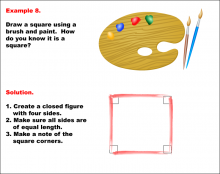
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 8 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 8TopicGeometry |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 9 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 9TopicGeometry DescriptionThe image shows a set of colorful stickers with various holiday-themed designs (hearts, snowmen, reindeer, bells, etc.). The stickers are arranged to form a square shape. The solution demonstrates how to use the stickers to create a square by aligning them in a closed figure with four clear corners. This example showcases how to draw a square using these stickers. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
|
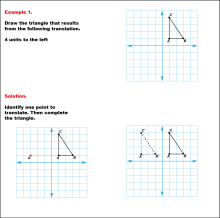
Math Example--Geometric Transformation--Translating Triangles--Example 1 | Math Example--Geometric Transformation--Translating Triangles--Example 1TopicTransformations DescriptionA triangle on a grid is translated 4 units to the left. It shows the original triangle ABC and the translated triangle A'B'C'. Example 1: "Draw the triangle that results from the following translation: 4 units to the left." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
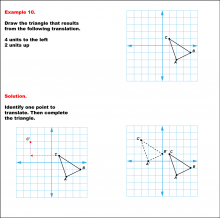
Math Example--Geometric Transformation--Translating Triangles--Example 10 | Math Example--Geometric Transformation--Translating Triangles--Example 10TopicTransformations Description
The triangle is translated 4 units to the left and 2 units up. It displays both the initial and the translated triangles. Example 10: "Draw the triangle that results from the following translation: 4 units to the left, 2 units up." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
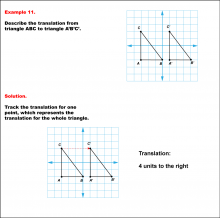
Math Example--Geometric Transformation--Translating Triangles--Example 11 | Math Example--Geometric Transformation--Translating Triangles--Example 11TopicTransformations DescriptionTriangle ABC is translated horizontally to the right by 4 units to form triangle A'B'C'. Example 11: The translation is described as 4 units to the right. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
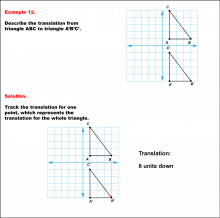
Math Example--Geometric Transformation--Translating Triangles--Example 12 | Math Example--Geometric Transformation--Translating Triangles--Example 12TopicTransformations DescriptionTriangle ABC is translated vertically downward by 6 units to form triangle A'B'C'. Example 12: The translation is described as 6 units down. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
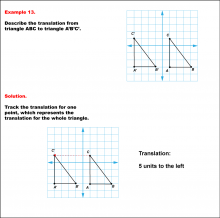
Math Example--Geometric Transformation--Translating Triangles--Example 13 | Math Example--Geometric Transformation--Translating Triangles--Example 13TopicTransformations DescriptionTriangle ABC is translated horizontally to the left by 5 units to form triangle A'B'C'. Example 13: The translation is described as 5 units to the left. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
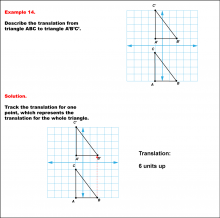
Math Example--Geometric Transformation--Translating Triangles--Example 14 | Math Example--Geometric Transformation--Translating Triangles--Example 14TopicTransformations DescriptionTriangle ABC is translated vertically upward by 6 units to form triangle A'B'C'. Example 14: The translation is described as 6 units up. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
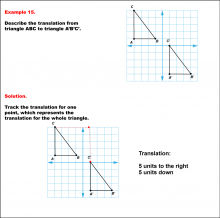
Math Example--Geometric Transformation--Translating Triangles--Example 15 | Math Example--Geometric Transformation--Translating Triangles--Example 15TopicTransformations Description
Triangle ABC is translated diagonally 5 units to the right and 5 units downward to form triangle A'B'C'. Example 15: The translation is described as 5 units to the right and 5 units down. |
Applications of Transformations and Applications of Triangles |
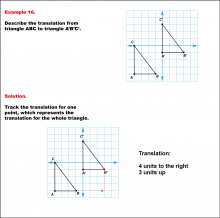
|
Math Example--Geometric Transformation--Translating Triangles--Example 16 | Math Example--Geometric Transformation--Translating Triangles--Example 16TopicTransformations DescriptionTriangle ABC is translated diagonally 4 units to the right and 3 units upward to form triangle A'B'C'. Example 16: The translation is described as 4 units to the right and 3 units up. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
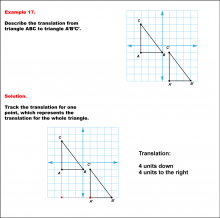
|
Math Example--Geometric Transformation--Translating Triangles--Example 17 | Math Example--Geometric Transformation--Translating Triangles--Example 17TopicTransformations DescriptionTriangle ABC is translated diagonally 4 units downward and 4 units to the right to form triangle A'B'C'. Example 17: The translation is described as 4 units down and 4 units to the right. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
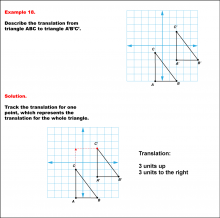
|
Math Example--Geometric Transformation--Translating Triangles--Example 18 | Math Example--Geometric Transformation--Translating Triangles--Example 18TopicTransformations Description
Triangle ABC is translated diagonally 3 units upward and 3 units to the right to form triangle A'B'C'. Example 18: The translation is described as 3 units up and 3 units to the right. |
Applications of Transformations and Applications of Triangles |
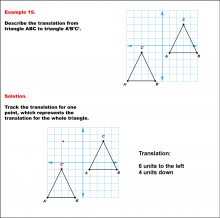
|
Math Example--Geometric Transformation--Translating Triangles--Example 19 | Math Example--Geometric Transformation--Translating Triangles--Example 19TopicTransformations DescriptionTriangle ABC is translated diagonally 6 units to the left and 4 units downward to form triangle A'B'C'. Example 19: The translation is described as 6 units to the left and 4 units down. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
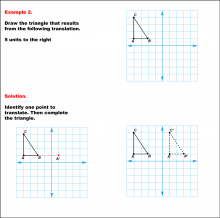
|
Math Example--Geometric Transformation--Translating Triangles--Example 2 | Math Example--Geometric Transformation--Translating Triangles--Example 2TopicTransformations DescriptionA triangle on a grid is translated 5 units to the right. The diagram shows the original triangle ABC and the new position, A'B'C'.. Example 2: "Draw the triangle that results from the following translation: 5 units to the right." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
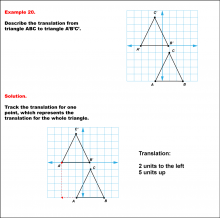
|
Math Example--Geometric Transformation--Translating Triangles--Example 20 | Math Example--Geometric Transformation--Translating Triangles--Example 20TopicTransformations DescriptionTriangle ABC is translated diagonally 2 units to the left and 5 units upward to form triangle A'B'C'. Example 20: The translation is described as 2 units to the left and 5 units up. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
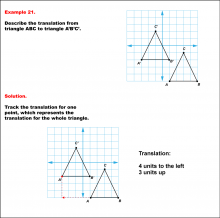
|
Math Example--Geometric Transformation--Translating Triangles--Example 21 | Math Example--Geometric Transformation--Translating Triangles--Example 21TopicTransformations |
Applications of Transformations and Applications of Triangles |
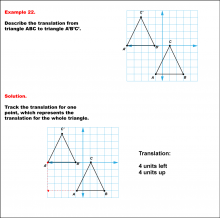
|
Math Example--Geometric Transformation--Translating Triangles--Example 22 | Math Example--Geometric Transformation--Translating Triangles--Example 22TopicTransformations |
Applications of Transformations and Applications of Triangles |
|
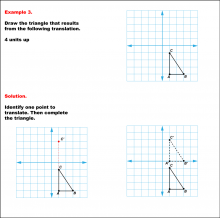
Math Example--Geometric Transformation--Translating Triangles--Example 3 | Math Example--Geometric Transformation--Translating Triangles--Example 3TopicTransformations DescriptionA triangle on a grid is translated 4 units up. The figure displays both the original and translated triangles ABC and A'B'C'.. Example 3: "Draw the triangle that results from the following translation: 4 units up." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
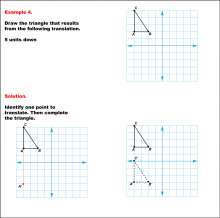
Math Example--Geometric Transformation--Translating Triangles--Example 4 | Math Example--Geometric Transformation--Translating Triangles--Example 4TopicTransformations DescriptionA triangle on a grid is translated 5 units down. It shows the original triangle and its new position after translation, labeled A'B'C'. Example 4: "Draw the triangle that results from the following translation: 5 units down." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
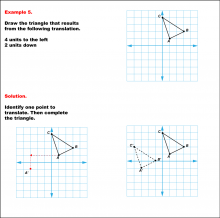
Math Example--Geometric Transformation--Translating Triangles--Example 5 | Math Example--Geometric Transformation--Translating Triangles--Example 5TopicTransformations DescriptionA triangle is translated 4 units to the left and 2 units down. Both the original and the new triangles, ABC and A'B'C', are illustrated. Example 5: "Draw the triangle that results from the following translation: 4 units to the left, 2 units down." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
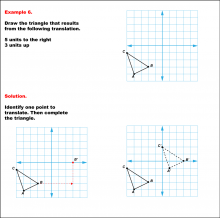
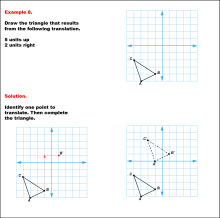
Math Example--Geometric Transformation--Translating Triangles--Example 6 | Math Example--Geometric Transformation--Translating Triangles--Example 6TopicTransformations DescriptionThe triangle is translated 5 units to the right and 3 units up. The image includes both original and translated triangles, labeled ABC and A'B'C'. Example 6: "Draw the triangle that results from the following translation: 5 units to the right, 3 units up." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
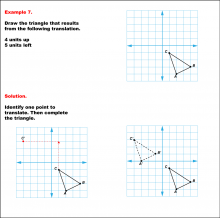
Math Example--Geometric Transformation--Translating Triangles--Example 7 | Math Example--Geometric Transformation--Translating Triangles--Example 7TopicTransformations DescriptionA triangle is translated 4 units up and 5 units left, showing the original ABC and translated A'B'C' triangles. Example 7: "Draw the triangle that results from the following translation: 4 units up, 5 units left." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
Math Example--Geometric Transformation--Translating Triangles--Example 8 | Math Example--Geometric Transformation--Translating Triangles--Example 8TopicTransformations Description
The triangle is translated 5 units up and 2 units right. The image shows both the original and translated positions of the triangle. Example 8: "Draw the triangle that results from the following translation: 5 units up, 2 units rogjt." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
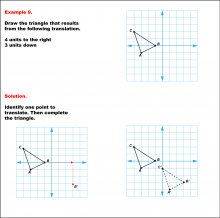
Math Example--Geometric Transformation--Translating Triangles--Example 9 | Math Example--Geometric Transformation--Translating Triangles--Example 9TopicTransformations DescriptionA triangle is translated 4 units to the right and 3 units down. The image shows both the original and the new triangle positions. Example 9: "Draw the triangle that results from the following translation: 4 units to the right, 3 units down." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
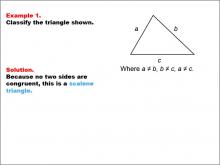
Math Example--Polygons--Triangle Classification: Example 1 | Math Example--Polygons--Triangle Classification: Example 1TopicTriangles DescriptionThis image shows a triangle with side lengths labeled as a, b, and c, where all sides are unequal. Based on the length of each side, the triangle is classified as scalene, as no two sides are congruent. Triangles are categorized based on side length (scalene, isosceles, equilateral) or angle measures (acute, obtuse, right). In this example, the scalene classification is determined by identifying that each side is a different length. The examples in this collection illustrate various classification rules based on both side and angle properties. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 10 | Math Example--Polygons--Triangle Classification: Example 10TopicTriangles DescriptionThis example presents a triangle with side lengths of 10, 10, and 8. Since two sides are congruent, the triangle is classified as isosceles. Triangle classification can be determined by side lengths or angle measures. Isosceles triangles have two equal sides or angles. Reviewing different examples assists students in identifying these types based on side or angle properties. Seeing multiple worked-out examples reinforces students’ ability to classify triangles by consistently applying classification rules. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 11 | Math Example--Polygons--Triangle Classification: Example 11TopicTriangles DescriptionThis example shows a triangle with two sides labeled as x and a third side labeled y. Because two sides are congruent, the triangle is classified as isosceles. Triangles can be classified by their side lengths or angle measures. An isosceles triangle has two equal sides or angles, as seen in this example. Reviewing a series of examples helps students understand these classifications and recognize patterns in triangles. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 12 | Math Example--Polygons--Triangle Classification: Example 12TopicTriangles DescriptionThis example shows a triangle with side lengths all equal to 9. Since all sides are congruent, the triangle is classified as equilateral. Triangles can be classified based on side or angle properties. An equilateral triangle has all sides and angles congruent. Viewing multiple examples reinforces students’ understanding of these classifications and enhances their ability to recognize triangle properties. Seeing several worked-out examples helps students understand and apply the rules consistently for classifying triangles. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 13 | Math Example--Polygons--Triangle Classification: Example 13TopicTriangles DescriptionThis example shows a triangle with three sides labeled as x, all equal in length. Since all sides are congruent, the triangle is classified as equilateral. Triangles can be categorized by side length or angle measures. An equilateral triangle has all congruent sides and angles. Reviewing multiple examples helps students recognize triangle classifications by observing side and angle patterns. Providing several examples reinforces students’ ability to consistently classify triangles based on the observed properties. |
Definition of a Triangle |
|
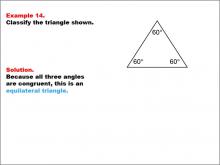
Math Example--Polygons--Triangle Classification: Example 14 | Math Example--Polygons--Triangle Classification: Example 14TopicTriangles DescriptionThis example shows a triangle with three angles, each measuring 60°. Since all angles are equal, the triangle is classified as equilateral. Triangle classification can be based on side lengths or angle measures. An equilateral triangle has all angles congruent. Reviewing examples like these helps students understand classification rules based on triangle properties. Multiple examples reinforce students' ability to identify triangle types consistently by observing angle or side characteristics. |
Definition of a Triangle |
|
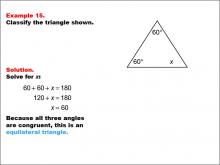
Math Example--Polygons--Triangle Classification: Example 15 | Math Example--Polygons--Triangle Classification: Example 15TopicTriangles DescriptionThis example presents a triangle with two angles labeled 60° and an unknown angle labeled x. Solving for x, we find it to be 60°, making all angles congruent and classifying the triangle as equilateral. Triangle classification can be determined by side length or angle measures. An equilateral triangle has all equal sides and angles. Observing multiple examples helps students apply these criteria consistently when classifying triangles. Seeing several worked examples helps students gain confidence in identifying triangles by recognizing congruent angles or sides. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 16 | Math Example--Polygons--Triangle Classification: Example 16TopicTriangles DescriptionThis example presents a triangle with three sides labeled as x, each equal in length. Since all three sides are congruent, the triangle is classified as equilateral. Triangles are categorized by their side lengths or angle measures. An equilateral triangle has all equal sides and angles, as seen in this example. Reviewing multiple examples reinforces students' understanding of the consistent characteristics that define each triangle type. Providing multiple worked-out examples helps students confidently apply classification rules to identify triangles by their properties. |
Definition of a Triangle |
|
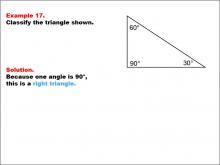
Math Example--Polygons--Triangle Classification: Example 17 | Math Example--Polygons--Triangle Classification: Example 17TopicTriangles DescriptionThis example shows a triangle with angles measuring 90°, 60°, and 30°. Since one angle is exactly 90°, the triangle is classified as a right triangle. Triangle classification often considers angle measures, with right triangles defined by having one 90° angle. Observing multiple examples allows students to consistently apply this classification rule. Reviewing various worked-out examples helps students solidify their understanding of identifying triangle types based on angle measurements. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 18 | Math Example--Polygons--Triangle Classification: Example 18TopicTriangles DescriptionThis example shows a triangle with two angles labeled 50° and 40° and an unknown angle x. Solving for x, we find it to be 90°, which classifies this as a right triangle. Triangles are classified by side lengths or angles, and a right triangle has a 90° angle. Examining examples like this helps students reinforce the criteria for identifying right triangles based on their angle properties. Seeing multiple worked-out examples enables students to apply classification rules more effectively and confidently. |
Definition of a Triangle |
|
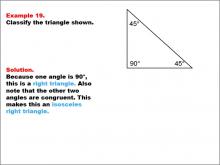
Math Example--Polygons--Triangle Classification: Example 19 | Math Example--Polygons--Triangle Classification: Example 19TopicTriangles DescriptionThis example presents a triangle with two congruent angles of 45° and one right angle of 90°. Because it has a 90° angle, the triangle is classified as a right triangle, and the two equal angles make it an isosceles right triangle. Triangle classification can involve side lengths or angles. A right triangle has a 90° angle, while isosceles triangles have two equal angles or sides. This example combines both classifications. Reviewing multiple examples helps students confidently apply the criteria to identify triangle types. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 2 | Math Example--Polygons--Triangle Classification: Example 2TopicTriangles DescriptionThis image shows a triangle with sides measuring 7, 8, and 9. The triangle is classified as scalene because each side has a different length, meaning no two sides are congruent. Triangles can be classified by examining their side lengths or angle measures. Scalene triangles, like the one shown, have no congruent sides, making them unique. This collection of examples helps students understand classification rules and visually identify different triangle types. |
Definition of a Triangle |

|
Math Example--Polygons--Triangle Classification: Example 20 | Math Example--Polygons--Triangle Classification: Example 20TopicTriangles DescriptionThis example shows a triangle with two known angles of 45° and an unknown angle x. Solving for x, we find it to be 90°, classifying this as a right triangle with two congruent angles, making it an isosceles right triangle. Triangle classification may be based on side lengths or angles. Right triangles have a 90° angle, while isosceles triangles have two equal sides or angles. Examples like this help students understand combined classifications. |
Definition of a Triangle |
|
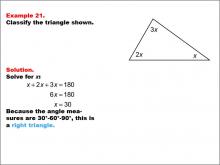
Math Example--Polygons--Triangle Classification: Example 21 | Math Example--Polygons--Triangle Classification: Example 21TopicTriangles DescriptionThis example shows a triangle with angles labeled as x, 2x, and 3x. Solving for x, we find that the angles are 30°, 60°, and 90°, classifying it as a right triangle. Triangle classification can involve angle measures or side lengths. Right triangles have one 90° angle, as seen here. Reviewing various examples supports students in consistently applying these classification rules. Observing multiple worked-out examples helps students gain confidence in identifying triangles based on the presence of specific angle measures. |
Definition of a Triangle |
|
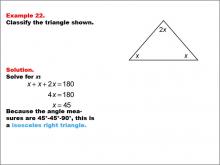
Math Example--Polygons--Triangle Classification: Example 22 | Math Example--Polygons--Triangle Classification: Example 22TopicTriangles DescriptionThis example shows a triangle with two equal angles labeled x and a third angle labeled 2x. Solving for x, we find the angles to be 45°, 45°, and 90°, classifying it as an isosceles right triangle. Triangles are classified by their angle measures or side lengths. Right triangles have a 90° angle, and isosceles triangles have two congruent angles. Reviewing examples like this one helps students understand combined classifications. |
Definition of a Triangle |
|
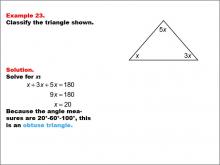
Math Example--Polygons--Triangle Classification: Example 23 | Math Example--Polygons--Triangle Classification: Example 23TopicTriangles DescriptionThis example shows a triangle with angles labeled x, 3x, and 5x. Solving for x, we find the angles to be 20°, 60°, and 100°, which classifies this triangle as obtuse because one of the angles is greater than 90°. Triangles can be classified by angle measures, with obtuse triangles defined as having one angle greater than 90°. Observing examples like this aids students in understanding how angle measures determine classifications. Providing multiple worked-out examples reinforces students' ability to consistently classify triangles based on angle properties. |
Definition of a Triangle |