
Illustrative Math Alignment: Grade 8 Unit 2
Dilations, Similarity, and Introducing Slope
Lesson 11: Writing Equations for Lines
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
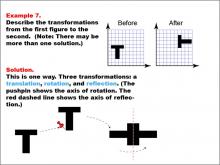
Math Example--Geometric Transformation--Transformations: Example 7 | Math Example--Geometric Transformation--Transformations: Example 7TopicTransformations DescriptionThis example illustrates a complex combination of transformations: translation, rotation, and reflection. Two grids labeled "Before" and "After" show a black "T" shape in different orientations. The solution diagram below demonstrates three sequential transformations: first, a translation moves the shape, then a rotation turns it (indicated by a pushpin showing the axis of rotation), and finally, a reflection flips it across a red dashed line representing the axis of reflection. |
Definition of Transformations |
|
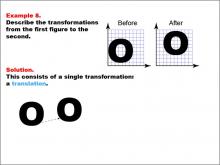
Math Example--Geometric Transformation--Transformations: Example 8 | Math Example--Geometric Transformation--Transformations: Example 8TopicTransformations DescriptionThis example demonstrates a simple translation in geometric transformations. Two grids labeled "Before" and "After" show an "O" shape slightly shifted between the grids. The solution diagram below illustrates a translation of the shape from one position to another, showcasing how an object can move position without changing its size or orientation. |
Definition of Transformations |
|
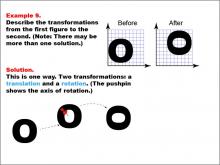
Math Example--Geometric Transformation--Transformations: Example 9 | Math Example--Geometric Transformation--Transformations: Example 9TopicTransformations DescriptionThis example illustrates a combination of transformations: translation and rotation. Two circular "O" shapes are shown on a grid, one labeled "Before" and the other "After". The solution involves a translation (movement) and a rotation, with a pushpin indicating the axis of rotation. This demonstrates how multiple transformations can be applied sequentially to a shape. |
Definition of Transformations |
|
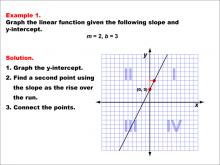
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 1 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 1TopicLinear Functions DescriptionThis example demonstrates how to graph a linear function with a slope of 2 and a y-intercept of 3. The process involves three key steps: first, plotting the y-intercept at (0, 3); second, using the slope to find another point on the line; and finally, connecting these points to form the line. |
Slope-Intercept Form |
|
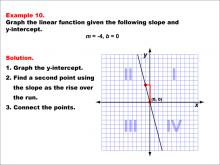
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 10 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 10TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of -4 and a y-intercept of 0. The method involves three main steps: plotting the y-intercept at the origin (0, 0), using the slope to determine a second point on the line, and connecting these points to create the linear graph. |
Slope-Intercept Form |
|
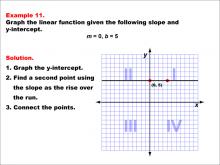
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 11 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 11TopicLinear Functions DescriptionThis example demonstrates the process of graphing a linear function with a slope of 0 and a y-intercept of 5. The procedure involves three key steps: plotting the y-intercept at (0, 5), recognizing that a slope of 0 results in a horizontal line, and drawing the line parallel to the x-axis through the y-intercept. |
Slope-Intercept Form |
|
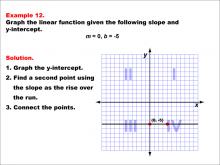
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 12 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 12TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of 0 and a y-intercept of -5. The method involves three main steps: plotting the y-intercept at (0, -5), recognizing that a slope of 0 results in a horizontal line, and drawing the line parallel to the x-axis through the y-intercept. |
Slope-Intercept Form |
|
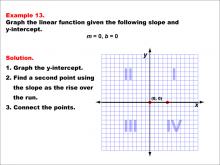
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 13 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 13TopicLinear Functions DescriptionThis example demonstrates how to graph a linear function with a slope of 0 and a y-intercept of 0. The process involves recognizing that this special case results in a horizontal line coinciding with the x-axis. The line passes through the origin (0, 0) and extends infinitely in both directions along the x-axis. |
Slope-Intercept Form |
|
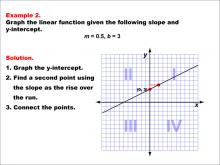
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 2 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 2TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of 0.5 and a y-intercept of 3. The method involves three main steps: plotting the y-intercept at (0, 3), using the slope to determine a second point on the line, and connecting these points to create the linear graph. |
Slope-Intercept Form |
|
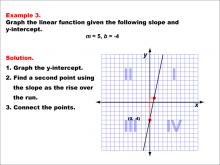
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 3 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 3TopicLinear Functions DescriptionThis example demonstrates the process of graphing a linear function with a slope of 5 and a y-intercept of -4. The procedure involves three key steps: plotting the y-intercept at (0, -4), using the slope to determine a second point on the line, and connecting these points to form the linear graph. |
Slope-Intercept Form |
|
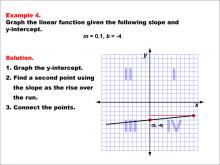
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 4 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 4TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of 0.1 and a y-intercept of -4. The method involves three main steps: plotting the y-intercept at (0, -4), using the slope to determine a second point on the line, and connecting these points to create the linear graph. |
Slope-Intercept Form |
|
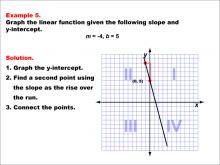
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 5 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 5TopicLinear Functions DescriptionThis example demonstrates how to graph a linear function with a slope of -4 and a y-intercept of 5. The process involves three key steps: first, plotting the y-intercept at (0, 5); second, using the slope to find another point on the line; and finally, connecting these points to form the line. |
Slope-Intercept Form |
|
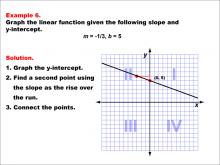
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 6 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 6TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of -1/3 and a y-intercept of 5. The method involves three main steps: plotting the y-intercept at (0, 5), using the slope to determine a second point on the line, and connecting these points to create the linear graph. |
Slope-Intercept Form |
|
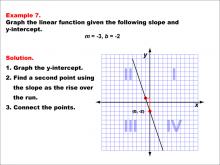
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 7 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 7TopicLinear Functions DescriptionThis example demonstrates the process of graphing a linear function with a slope of -3 and a y-intercept of -2. The procedure involves three key steps: plotting the y-intercept at (0, -2), using the slope to determine a second point on the line, and connecting these points to form the linear graph. |
Slope-Intercept Form |
|
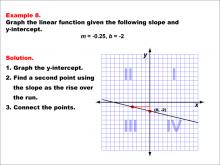
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 8 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 8TopicLinear Functions DescriptionThis example illustrates the process of graphing a linear function with a slope of -0.25 and a y-intercept of -2. The method involves three main steps: plotting the y-intercept at (0, -2), using the slope to determine a second point on the line, and connecting these points to create the linear graph. |
Slope-Intercept Form |
|
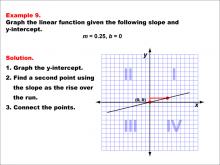
Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 9 | Math Example--Linear Function Concepts--Graphs of Linear Functions in Slope-Intercept Form: Example 9TopicLinear Functions DescriptionThis example demonstrates how to graph a linear function with a slope of 0.25 and a y-intercept of 0. The process involves three key steps: first, plotting the y-intercept at the origin (0, 0); second, using the slope to find another point on the line; and finally, connecting these points to form the line. |
Slope-Intercept Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 1TopicLinear Functions DescriptionThis example demonstrates the process of converting a linear equation from standard form to slope-intercept form. The equation 2x + 4y = 8 is solved step-by-step, isolating y and dividing by its coefficient. The result is y = -1/2 x + 2, clearly showing the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 10 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 10TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation x + y = 1 from standard form to slope-intercept form. The process involves isolating y, resulting in y = -x + 1. This simple transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 11 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 11TopicLinear Functions DescriptionThis example showcases the transformation of the linear equation x + y = -1 from standard form to slope-intercept form. The process involves isolating y, resulting in y = -x - 1. This step-by-step solution clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 12 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 12TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation x - y = 1 from standard form to slope-intercept form. The solution process involves isolating y and changing the sign of both sides, resulting in y = x - 1. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 13 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 13TopicLinear Functions DescriptionThis example illustrates the process of converting the linear equation -x + y = 1 from standard form to slope-intercept form. The solution involves rearranging the equation to isolate y, resulting in y = x + 1. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 14 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 14TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -x - y = -1 from standard form to slope-intercept form. The process involves manipulating the equation to solve for y, yielding y = -x + 1. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 15 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 15TopicLinear Functions DescriptionThis example showcases the transformation of the linear equation -x - y = 1 from standard form to slope-intercept form. The solution process involves isolating y, resulting in y = -x - 1. This step-by-step conversion clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 16 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 16TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -x + y = -1 from standard form to slope-intercept form. The process involves isolating y, resulting in y = x - 1. This transformation clearly reveals the slope and y-intercept of the line. Linear functions are fundamental mathematical concepts that describe relationships between two variables. The examples in this collection, such as showing step-by-step transformations from standard form to slope-intercept form, help in understanding how each part of the equation affects the graph and the relationship itself. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 17 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 17TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation x - y = -1 from standard form to slope-intercept form. The solution involves isolating y, resulting in y = x + 1. This process clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 18 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 18TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -x - y = 1 from standard form to slope-intercept form. The process involves rearranging the equation to isolate y, resulting in y = -x - 1. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 19 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 19TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation 12x + 28y = 0 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = -3/7 x. This process clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 2 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 2TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation 3x + 6y = -18 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = -1/2 x - 3. This process clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 20 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 20TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -14x - 35y = 0 from standard form to slope-intercept form. The process involves isolating y and dividing by its coefficient, resulting in y = -2/5 x. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 21 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 21TopicLinear Functions DescriptionThis example showcases the transformation of the linear equation 28x - 21y = 0 from standard form to slope-intercept form. The process involves isolating y and dividing by its coefficient, resulting in y = 4/3 x. This step-by-step solution clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 22 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 22TopicLinear Functions DescriptionThis example illustrates the conversion of the linear equation -13x + 39y = 0 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = 1/3 x. This process clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 3 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 3TopicLinear Functions DescriptionThis example showcases the transformation of the linear equation 5x - 2y = 12 from standard form to slope-intercept form. The process involves isolating y and dividing by its coefficient, resulting in y = 2.5x - 6. This step-by-step solution clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 4 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 4TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -6x + 10y = 20 from standard form to slope-intercept form. The solution process involves isolating y and dividing by its coefficient, resulting in y = 0.6x + 2. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 5 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 5TopicLinear Functions DescriptionThis example illustrates the process of converting the linear equation -9x - 15y = -45 from standard form to slope-intercept form. The solution involves rearranging the equation to isolate y, resulting in y = 3/5 x + 3. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 6 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 6TopicLinear Functions DescriptionThis example demonstrates the conversion of the linear equation -8x - 12y = 25 from standard form to slope-intercept form. The process involves manipulating the equation to solve for y, yielding y = -2/3 x - 25/12. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 7 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 7TopicLinear Functions DescriptionThis example illustrates the transformation of the linear equation -2x + 16y = -36 from standard form to slope-intercept form. The solution process involves solving for y, resulting in y = 1/8 x - 9/4. This step-by-step conversion clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 8 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 8TopicLinear Functions DescriptionThis example showcases the conversion of the linear equation -7x + 21y = 63 from standard form to slope-intercept form. The process involves rearranging the equation to isolate y, resulting in y = 1/3 x + 3. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |

|
Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 9 | Math Example--Linear Function Concepts--Linear Equations in Standard Form: Example 9TopicLinear Functions DescriptionThis example demonstrates the process of converting the linear equation 10x - 28y = 56 from standard form to slope-intercept form. The solution involves isolating y and dividing by its coefficient, resulting in y = (5/14)x - 2. This transformation clearly reveals the slope and y-intercept of the line. |
Standard Form |
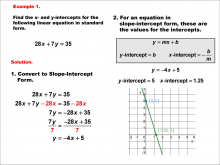
|
Math Example--Linear Function Concepts--Linear Intercepts: Example 1 | Math Example--Linear Function Concepts--Linear Intercepts: Example 1TopicLinear Functions DescriptionFind the x- and y-intercepts for the linear equation 28x + 7y = 35 given in standard form. Convert it to slope-intercept form. The equation is rewritten as y = -4x + 5 by isolating y. The y-intercept is found as 5 (where x = 0), and the x-intercept is calculated as 1.25 (where y = 0). These intercepts are plotted on a graph. Linear functions are a fundamental concept in algebra, where we explore the relationships between variables. The examples in this collection highlight how to find intercepts and analyze the relationships they represent in a linear context. |
Slope-Intercept Form and Standard Form |
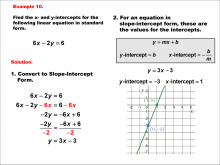
|
Math Example--Linear Function Concepts--Linear Intercepts: Example 10 | Math Example--Linear Function Concepts--Linear Intercepts: Example 10TopicLinear Functions DescriptionFind the x- and y-intercepts for the linear equation 6x - 2y = 6 given in standard form. Convert it to slope-intercept form. The equation is rewritten as y = 3x - 3. The y-intercept is -3 (where x = 0), and the x-intercept is 1 (where y = 0). These intercepts are plotted on a graph. Linear functions are a fundamental concept in algebra, where we explore the relationships between variables. The examples in this collection highlight how to find intercepts and analyze the relationships they represent in a linear context. |
Slope-Intercept Form and Standard Form |
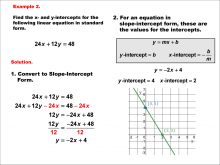
|
Math Example--Linear Function Concepts--Linear Intercepts: Example 2 | Math Example--Linear Function Concepts--Linear Intercepts: Example 2TopicLinear Functions DescriptionFind the x- and y-intercepts for the linear equation 24x + 12y = 48 given in standard form. Convert it to slope-intercept form. The equation is rewritten as y = -2x + 4. The y-intercept is 4 (where x = 0), and the x-intercept is 2 (where y = 0). These intercepts are plotted on a graph. Linear functions are a fundamental concept in algebra, where we explore the relationships between variables. The examples in this collection highlight how to find intercepts and analyze the relationships they represent in a linear context. |
Slope-Intercept Form and Standard Form |
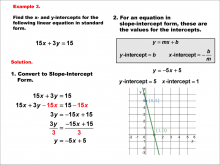
|
Math Example--Linear Function Concepts--Linear Intercepts: Example 3 | Math Example--Linear Function Concepts--Linear Intercepts: Example 3TopicLinear Functions DescriptionFind the x- and y-intercepts for the linear equation 15x + 3y = 15 given in standard form. Convert it to slope-intercept form. The equation is rewritten as y = -5x + 5. The y-intercept is 5 (where x = 0), and the x-intercept is 1 (where y = 0). These intercepts are plotted on a graph. Linear functions are a fundamental concept in algebra, where we explore the relationships between variables. The examples in this collection highlight how to find intercepts and analyze the relationships they represent in a linear context. |
Slope-Intercept Form and Standard Form |
|
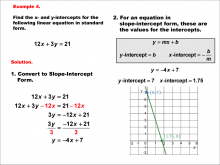
Math Example--Linear Function Concepts--Linear Intercepts: Example 4 | Math Example--Linear Function Concepts--Linear Intercepts: Example 4TopicLinear Functions DescriptionFind the x- and y-intercepts for the linear equation 12x + 3y = 21 given in standard form. Convert it to slope-intercept form. The equation is rewritten as y = -4x + 7. The y-intercept is 7 (where x = 0), and the x-intercept is 1.75 (where y = 0). These intercepts are plotted on a graph. Linear functions are a fundamental concept in algebra, where we explore the relationships between variables. The examples in this collection highlight how to find intercepts and analyze the relationships they represent in a linear context. |
Slope-Intercept Form and Standard Form |
|
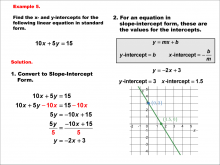
Math Example--Linear Function Concepts--Linear Intercepts: Example 5 | Math Example--Linear Function Concepts--Linear Intercepts: Example 5TopicLinear Functions DescriptionFind the x- and y-intercepts for the linear equation 10x + 5y = 15 given in standard form. Convert it to slope-intercept form. The equation is rewritten as y = -2x + 3. The y-intercept is 3 (where x = 0), and the x-intercept is 1.5 (where y = 0). These intercepts are plotted on a graph. Linear functions are a fundamental concept in algebra, where we explore the relationships between variables. The examples in this collection highlight how to find intercepts and analyze the relationships they represent in a linear context. |
Slope-Intercept Form and Standard Form |
|
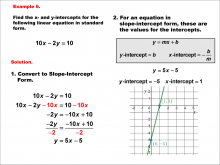
Math Example--Linear Function Concepts--Linear Intercepts: Example 6 | Math Example--Linear Function Concepts--Linear Intercepts: Example 6TopicLinear Functions DescriptionFind the x- and y-intercepts for the linear equation 10x - 2y = 10 given in standard form. Convert it to slope-intercept form. The equation is rewritten as y = 5x - 5. The y-intercept is -5 (where x = 0), and the x-intercept is 1 (where y = 0). These intercepts are plotted on a graph. Linear functions are a fundamental concept in algebra, where we explore the relationships between variables. The examples in this collection highlight how to find intercepts and analyze the relationships they represent in a linear context. |
Slope-Intercept Form and Standard Form |
|
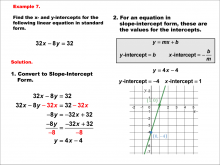
Math Example--Linear Function Concepts--Linear Intercepts: Example 7 | Math Example--Linear Function Concepts--Linear Intercepts: Example 7TopicLinear Functions DescriptionFind the x- and y-intercepts for the linear equation 32x - 8y = 32 given in standard form. Convert it to slope-intercept form. The equation is rewritten as y = 4x - 4. The y-intercept is -4 (where x = 0), and the x-intercept is 1 (where y = 0). These intercepts are plotted on a graph. Linear functions are a fundamental concept in algebra, where we explore the relationships between variables. The examples in this collection highlight how to find intercepts and analyze the relationships they represent in a linear context. |
Slope-Intercept Form and Standard Form |
|
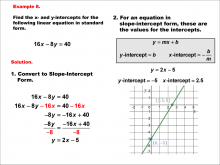
Math Example--Linear Function Concepts--Linear Intercepts: Example 8 | Math Example--Linear Function Concepts--Linear Intercepts: Example 8TopicLinear Functions DescriptionFind the x- and y-intercepts for the linear equation 16x - 8y = 40 given in standard form. Convert it to slope-intercept form. The equation is rewritten as y = 2x - 5. The y-intercept is -5 (where x = 0), and the x-intercept is 2.5 (where y = 0). These intercepts are plotted on a graph. Linear functions are a fundamental concept in algebra, where we explore the relationships between variables. The examples in this collection highlight how to find intercepts and analyze the relationships they represent in a linear context. |
Slope-Intercept Form and Standard Form |
|
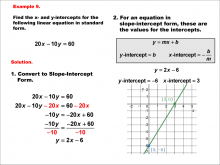
Math Example--Linear Function Concepts--Linear Intercepts: Example 9 | Math Example--Linear Function Concepts--Linear Intercepts: Example 9TopicLinear Functions DescriptionFind the x- and y-intercepts for the linear equation 20x - 10y = 60 given in standard form. Convert it to slope-intercept form. The equation is rewritten as y = 2x - 6. The y-intercept is -6 (where x = 0), and the x-intercept is 3 (where y = 0). These intercepts are plotted on a graph. Linear functions are a fundamental concept in algebra, where we explore the relationships between variables. The examples in this collection highlight how to find intercepts and analyze the relationships they represent in a linear context. |
Slope-Intercept Form and Standard Form |
|
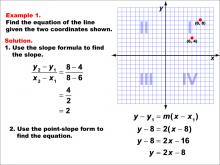
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 1 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 1TopicLinear Functions DescriptionThis example demonstrates how to find the equation of a line passing through two given points: (6, 4) and (8, 8). The slope is calculated using the formula (y2 - y1) / (x2 - x1), resulting in a slope of 2. Using the point-slope form of a line, y - y1 = m(x - x1), the equation is derived as y - 8 = 2(x - 8), which simplifies to y = 2x - 8. |
Point-Slope Form and Slope-Intercept Form |
|
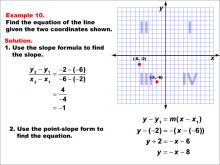
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 10 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 10TopicLinear Functions DescriptionThe image shows a coordinate plane with two points (-6, -2) and (-2, -6) marked. It provides a step-by-step solution to find the equation of the line passing through these points. The slope is calculated, and the equation is derived using point-slope form. The slope is calculated as (y2 - y1) / (x2 - x1) = (-6 - (-2)) / (-2 - (-6)) = -4 / 4 = -1. Using point-slope form, y - y1 = m(x - x1), the equation is derived as y + 2 = -(x + 6), which simplifies to y = -x - 8. |
Point-Slope Form and Slope-Intercept Form |