
Illustrative Math Alignment: Grade 8 Unit 2
Dilations, Similarity, and Introducing Slope
Lesson 8: Similar Triangles
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
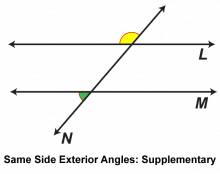
Math Clip Art: Parallel Lines Cut by a Transversal 20 | Math Clip Art: Parallel Lines Cut by a Transversal 20TopicGeometry DescriptionThis math clip art image is the final in a series illustrating the properties of parallel lines cut by a transversal. It focuses on another pair of same side exterior angles, reinforcing the concept that these angles are supplementary when parallel lines are cut by a transversal. The image uses distinct color coding to identify this second pair of same side exterior angles, providing students with a comprehensive view of all angle relationships in this configuration. |
Parallel Lines |
|
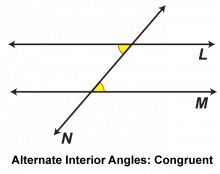
Math Clip Art: Parallel Lines Cut by a Transversal 3 | Math Clip Art: Parallel Lines Cut by a Transversal 3TopicGeometry DescriptionThis math clip art image is part of a series illustrating the properties of parallel lines cut by a transversal. It specifically highlights alternate interior angles, showing that they are congruent when parallel lines are cut by a transversal. The image uses color coding to clearly identify the alternate interior angles, making it easier for students to visualize this important geometric relationship. |
Parallel Lines |
|
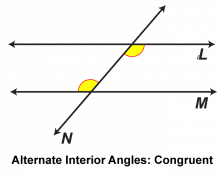
Math Clip Art: Parallel Lines Cut by a Transversal 4 | Math Clip Art: Parallel Lines Cut by a Transversal 4TopicGeometry DescriptionThis math clip art image is part of a series illustrating the properties of parallel lines cut by a transversal. It focuses on another pair of alternate interior angles, reinforcing the concept that these angles are congruent when parallel lines are cut by a transversal. The image uses distinct color coding to identify this second pair of alternate interior angles, providing students with a clear visual representation of this geometric relationship. |
Parallel Lines |
|
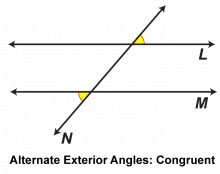
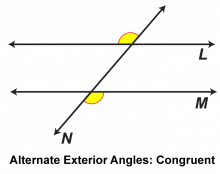
Math Clip Art: Parallel Lines Cut by a Transversal 5 | Math Clip Art: Parallel Lines Cut by a Transversal 5TopicGeometry DescriptionThis math clip art image is part of a series illustrating the properties of parallel lines cut by a transversal. It highlights alternate exterior angles, demonstrating that these angles are congruent when parallel lines are cut by a transversal. The image uses color coding to clearly identify the alternate exterior angles, making it easier for students to visualize and understand this geometric relationship. |
Parallel Lines |
|
Math Clip Art: Parallel Lines Cut by a Transversal 6 | Math Clip Art: Parallel Lines Cut by a Transversal 6TopicGeometry DescriptionThis math clip art image is part of a series illustrating the properties of parallel lines cut by a transversal. It focuses on alternate exterior angles, demonstrating that these angles are congruent when parallel lines are cut by a transversal. The image uses color coding to clearly identify another pair of alternate exterior angles, reinforcing the concept introduced in the previous image. |
Parallel Lines |
|
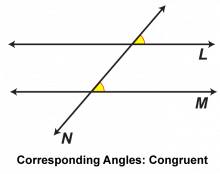
Math Clip Art: Parallel Lines Cut by a Transversal 7 | Math Clip Art: Parallel Lines Cut by a Transversal 7TopicGeometry DescriptionThis math clip art image is part of a series illustrating the properties of parallel lines cut by a transversal. It highlights corresponding angles, demonstrating that these angles are congruent when parallel lines are cut by a transversal. The image uses color coding to clearly identify a pair of corresponding angles, making it easier for students to visualize and understand this geometric relationship. |
Parallel Lines |
|
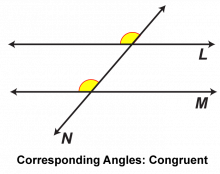
Math Clip Art: Parallel Lines Cut by a Transversal 8 | Math Clip Art: Parallel Lines Cut by a Transversal 8TopicGeometry DescriptionThis math clip art image is part of a series illustrating the properties of parallel lines cut by a transversal. It focuses on another pair of corresponding angles, reinforcing the concept that these angles are congruent when parallel lines are cut by a transversal. The image uses distinct color coding to identify this second pair of corresponding angles, providing students with a clear visual representation of this geometric relationship. |
Parallel Lines |
|
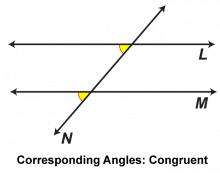
Math Clip Art: Parallel Lines Cut by a Transversal 9 | Math Clip Art: Parallel Lines Cut by a Transversal 9TopicGeometry DescriptionThis math clip art image is part of a series illustrating the properties of parallel lines cut by a transversal. It highlights yet another pair of corresponding angles, further reinforcing the concept that these angles are congruent when parallel lines are cut by a transversal. The image uses a unique color coding to identify this third pair of corresponding angles, providing students with multiple examples of this geometric relationship. |
Parallel Lines |
|
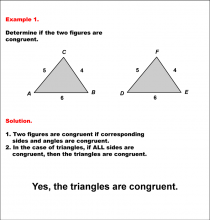
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 1TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF also has sides 5, 4, and 6. The SSS Postulate ensures that these triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
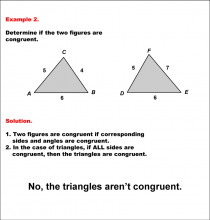
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 2TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5, 4, and 6, while triangle DEF has sides 5, 7, and 6. Because corresponding sides are not all congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
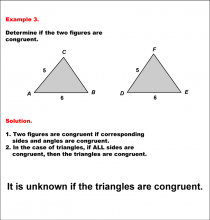
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 3TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6, and triangle DEF has sides 5 and 6, but no information on the third side. As a result, there isn't enough information to know if they are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 4TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Both triangles have two sides (5 and 6) and an included angle of 60°. As a results of the SAS Postulate, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 5TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Triangle ABC has sides 5 and 6 with an included angle of 60°, and triangle DEF has sides 5 and 6 with an included angle of 62°. Because corresponding angles are not congruent, then the triangles are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 6TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are congruent. Both triangles have angles of 63°, 60°, and 57°, but no information on side lengths. As a result, we can't conclude if the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 7TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. Both triangles appear identical in shape and orientation, positioned differently on the grid. Using the grid, you can see that corresponding sides are congruent. Therefore the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 8TopicGeometric Shapes DescriptionDetermine if two shapes on a grid are congruent. The shapes appear as two congruent triangles within a diamond shape, with each triangle reflected across the center axis. Using the grid, you can see that corresonding sides are congruent. Therefore, the triangles are congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9 | Math Example--Geometric Shapes--Analyzing Congruent Shapes--Example 9TopicGeometric Shapes DescriptionDetermine if two triangles on a grid are congruent. The triangles have differing shapes and orientations on the grid, suggesting different side lengths or angles. Therefore, they are not congruent. Congruence of shapes is fundamental in geometry as it allows us to establish relationships between figures and understand properties of transformations. This example collection illustrates congruence by analyzing side lengths and angles to determine equivalence. |
Definition of a Triangle |
|
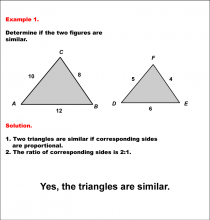
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 1 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 1TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10, 8, and 12, while triangle DEF has sides 5, 4, and 6. Triangles are similar if corresponding sides are proportional. Here, the ratio of corresponding sides is 2:1 (10:5, 8:4, 12:6). Thus, the triangles are similar. Therefore, the answer is Yes, the triangles are similar. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 10 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 10TopicGeometric Shapes DescriptionDetermine if two right triangles are similar. The triangle on the left has angle 40°, and the other triangle has a 60° angle. For similarity, all corresponding angles must be congruent. The angles in each triangle do not match, so the triangles aren't similar. Therefore, the answer is No, the triangles aren't similar. |
Definition of a Triangle |
|
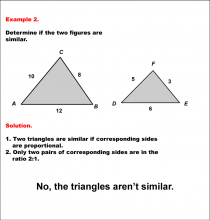
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 2 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 2TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10, 8, and 12, while triangle DEF has sides 5, 3, and 6. Triangles are similar if all corresponding sides are proportional. Only two pairs of sides here have a 2:1 ratio, so the triangles are not similar. Therefore, the answer is No, the triangles arenÕt similar. |
Definition of a Triangle |
|
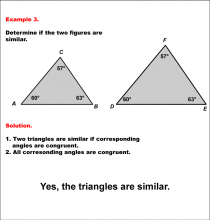
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 3 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 3TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Both triangles have angles 60°, 57°, and 63°. Triangles are similar if corresponding angles are equal. Since all corresponding angles match, the triangles are similar. Therefore, the answer is Yes, the triangles are similar. Understanding the concept of geometric shapes is essential for developing geometric reasoning. These examples demonstrate how to analyze and verify similarity between shapes by comparing corresponding sides and angles. The worked-out examples provided help students visualize and understand this key concept. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 4 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 4TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has angles 75°, 42°, and an unknown angle, and triangle DEF has angles 75° and 63° and an unknown angles. Triangles are similar if all corresponding angles are congruent. Solving for the unknown angles confirms angle congruency, so the triangles are similar. Therefore, the answer is Yes, the triangles are similar. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 5 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 5TopicGeometric Shapes DescriptionDetermine if two right triangles, ABC and DEF, are similar. Triangle ABC has angles 90° and 40°, and triangle DEF has angles 90° and 50°. Triangles are similar if all corresponding angles are congruent. Solving reveals congruent corresponding angles. Therefore, the answer is Yes, the triangles are similar. Understanding the concept of geometric shapes is essential for developing geometric reasoning. These examples demonstrate how to analyze and verify similarity between shapes by comparing corresponding sides and angles. The worked-out examples provided help students visualize and understand this key concept. |
Definition of a Triangle |

|
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 6 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 6TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has a right angle and an angle of 40°, and triangle DEF has a right angle and 45°. Not all corresponding angles are congruent, so the triangles are not similar. Therefore, the answer is No, the triangles aren't similar. Understanding the concept of geometric shapes is essential for developing geometric reasoning. These examples demonstrate how to analyze and verify similarity between shapes by comparing corresponding sides and angles. The worked-out examples provided help students visualize and understand this key concept. |
Definition of a Triangle |
|
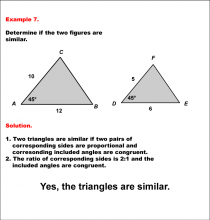
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 7 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 7TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10 and 12 with a 45° angle, and triangle DEF has sides 5 and 6 with a 45° angle. Triangles are similar if two pairs of sides are proportional, and the included angle is congruent. The side ratio is 2:1, and both included angles are 45°. Therefore, the answer is Yes, the triangles are similar. |
Definition of a Triangle |
|
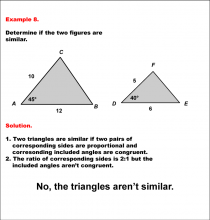
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 8 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 8TopicGeometric Shapes DescriptionDetermine if two triangles, ABC and DEF, are similar. Triangle ABC has sides 10 and 12 with a 45° angle, and triangle DEF has sides 5 and 6 with a 40° angle. Triangles are similar if two pairs of sides are proportional, and the included angles are congruent. Here, the included angles differ (45° vs. 40°), so the triangles are not similar. Therefore, the answer is No, the triangles aren't similar. |
Definition of a Triangle |
|
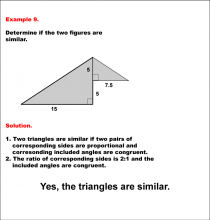
Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 9 | Math Example--Geometric Shapes--Analyzing Similar Shapes--Example 9TopicGeometric Shapes DescriptionDetermine if two right triangles are similar. The triangle on the left has sides 10 and 15 and an included right angle, while the other triangle has sides 5 and 7.5 and an included right angle. Triangles are similar if two pairs of corresponding sides are proportional, and corresponding included angles are congruent. The side ratio is 2:1, and the included right angles are congruent. Therefore, the answer is Yes, the triangles are similar. |
Definition of a Triangle |
|
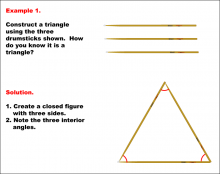
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 1 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 1TopicGeometry DescriptionThis image shows three drumsticks arranged to form a triangle. The drumsticks are placed in a closed triangular shape, with three angles marked in red. This example shows how to construct a triangle using drumsticks. The solution explains that to know it's a triangle, you need to create a closed figure with three sides and note the three interior angles. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
|
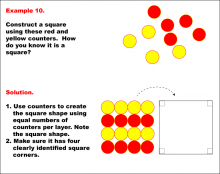
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 10 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 10TopicGeometry DescriptionThe image shows red and yellow circular counters arranged in a grid pattern to form a square shape. The solution explains how to arrange the counters in equal numbers per layer to form a square with four clearly defined corners. This example showcases how to construct a square using these red and yellow counters. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 2 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 2TopicGeometry DescriptionThis image shows a triangle drawn using a crayon. The triangle is closed with three sides, and the three angles are highlighted in red. This example showcases how to draw a triangle using a crayon or pencil. The solution states that to confirm it's a triangle, you need to create a closed figure with three sides and ensure it has three clearly identified angles. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
|
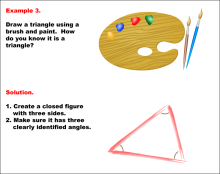
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 3 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 3TopicGeometry DescriptionThis image shows a triangle drawn using paint and a brush. The triangle is closed with three sides, and the three angles are marked in red. This example showcases how to draw a triangle using paint and a brush. The solution explains that to verify it's a triangle, you must create a closed figure with three sides and make sure it has three clearly identified angles. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 4 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 4TopicGeometry DescriptionThis image shows a triangle formed by arranging stickers in a triangular shape. The stickers form the sides of the triangle, and the angles are highlighted. This example showcases how to draw a triangle using stickers. The solution mentions that you can use stickers to form a closed figure with three sides, ensuring it has three clearly identified angles to confirm it's a triangle. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
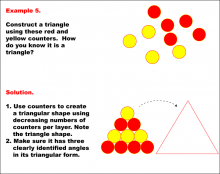
|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 5 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 5TopicGeometry |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 6 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 6TopicGeometry DescriptionThe image features four drumsticks arranged in a square shape. The solution highlights how to verify that the figure is a square by checking that it has four sides and four square corners. This example showcases how to construct a square using four drumsticks. The text describes how to create a closed figure with four sides and check for square corners to confirm it's a square. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 7 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 7TopicGeometry |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
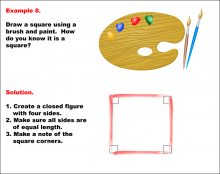
|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 8 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 8TopicGeometry |
Definition of a Quadrilateral and Geometric Constructions with Triangles |

|
Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 9 | Math Example--Geometric Shapes--Constructing Geometric Shapes: Example 9TopicGeometry DescriptionThe image shows a set of colorful stickers with various holiday-themed designs (hearts, snowmen, reindeer, bells, etc.). The stickers are arranged to form a square shape. The solution demonstrates how to use the stickers to create a square by aligning them in a closed figure with four clear corners. This example showcases how to draw a square using these stickers. |
Definition of a Quadrilateral and Geometric Constructions with Triangles |
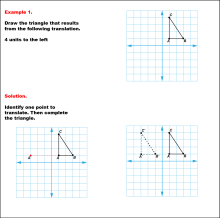
|
Math Example--Geometric Transformation--Translating Triangles--Example 1 | Math Example--Geometric Transformation--Translating Triangles--Example 1TopicTransformations DescriptionA triangle on a grid is translated 4 units to the left. It shows the original triangle ABC and the translated triangle A'B'C'. Example 1: "Draw the triangle that results from the following translation: 4 units to the left." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
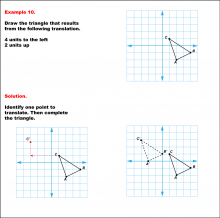
|
Math Example--Geometric Transformation--Translating Triangles--Example 10 | Math Example--Geometric Transformation--Translating Triangles--Example 10TopicTransformations Description
The triangle is translated 4 units to the left and 2 units up. It displays both the initial and the translated triangles. Example 10: "Draw the triangle that results from the following translation: 4 units to the left, 2 units up." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
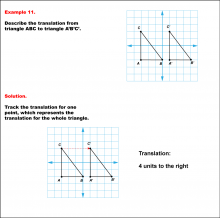
Math Example--Geometric Transformation--Translating Triangles--Example 11 | Math Example--Geometric Transformation--Translating Triangles--Example 11TopicTransformations DescriptionTriangle ABC is translated horizontally to the right by 4 units to form triangle A'B'C'. Example 11: The translation is described as 4 units to the right. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
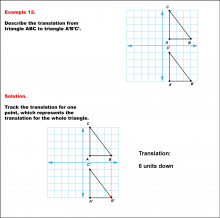
Math Example--Geometric Transformation--Translating Triangles--Example 12 | Math Example--Geometric Transformation--Translating Triangles--Example 12TopicTransformations DescriptionTriangle ABC is translated vertically downward by 6 units to form triangle A'B'C'. Example 12: The translation is described as 6 units down. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
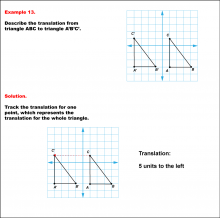
Math Example--Geometric Transformation--Translating Triangles--Example 13 | Math Example--Geometric Transformation--Translating Triangles--Example 13TopicTransformations DescriptionTriangle ABC is translated horizontally to the left by 5 units to form triangle A'B'C'. Example 13: The translation is described as 5 units to the left. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
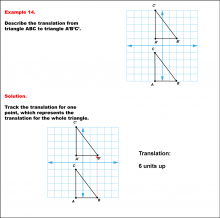
Math Example--Geometric Transformation--Translating Triangles--Example 14 | Math Example--Geometric Transformation--Translating Triangles--Example 14TopicTransformations DescriptionTriangle ABC is translated vertically upward by 6 units to form triangle A'B'C'. Example 14: The translation is described as 6 units up. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
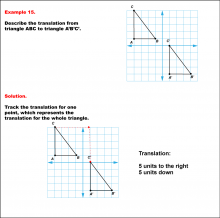
|
Math Example--Geometric Transformation--Translating Triangles--Example 15 | Math Example--Geometric Transformation--Translating Triangles--Example 15TopicTransformations Description
Triangle ABC is translated diagonally 5 units to the right and 5 units downward to form triangle A'B'C'. Example 15: The translation is described as 5 units to the right and 5 units down. |
Applications of Transformations and Applications of Triangles |
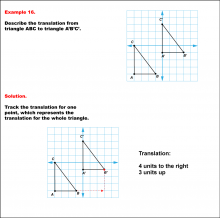
|
Math Example--Geometric Transformation--Translating Triangles--Example 16 | Math Example--Geometric Transformation--Translating Triangles--Example 16TopicTransformations DescriptionTriangle ABC is translated diagonally 4 units to the right and 3 units upward to form triangle A'B'C'. Example 16: The translation is described as 4 units to the right and 3 units up. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
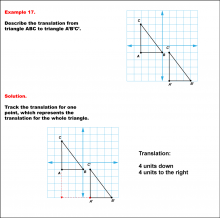
|
Math Example--Geometric Transformation--Translating Triangles--Example 17 | Math Example--Geometric Transformation--Translating Triangles--Example 17TopicTransformations DescriptionTriangle ABC is translated diagonally 4 units downward and 4 units to the right to form triangle A'B'C'. Example 17: The translation is described as 4 units down and 4 units to the right. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
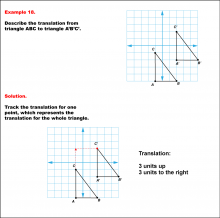
|
Math Example--Geometric Transformation--Translating Triangles--Example 18 | Math Example--Geometric Transformation--Translating Triangles--Example 18TopicTransformations Description
Triangle ABC is translated diagonally 3 units upward and 3 units to the right to form triangle A'B'C'. Example 18: The translation is described as 3 units up and 3 units to the right. |
Applications of Transformations and Applications of Triangles |
|
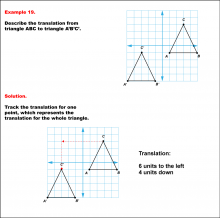
Math Example--Geometric Transformation--Translating Triangles--Example 19 | Math Example--Geometric Transformation--Translating Triangles--Example 19TopicTransformations DescriptionTriangle ABC is translated diagonally 6 units to the left and 4 units downward to form triangle A'B'C'. Example 19: The translation is described as 6 units to the left and 4 units down. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |
|
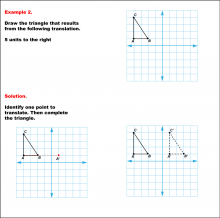
Math Example--Geometric Transformation--Translating Triangles--Example 2 | Math Example--Geometric Transformation--Translating Triangles--Example 2TopicTransformations DescriptionA triangle on a grid is translated 5 units to the right. The diagram shows the original triangle ABC and the new position, A'B'C'.. Example 2: "Draw the triangle that results from the following translation: 5 units to the right." Solution: "Identify one point to translate. Then complete the triangle." |
Applications of Transformations and Applications of Triangles |
|
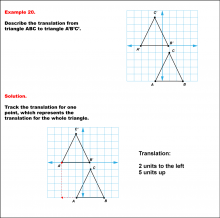
Math Example--Geometric Transformation--Translating Triangles--Example 20 | Math Example--Geometric Transformation--Translating Triangles--Example 20TopicTransformations DescriptionTriangle ABC is translated diagonally 2 units to the left and 5 units upward to form triangle A'B'C'. Example 20: The translation is described as 2 units to the left and 5 units up. In this topic, students explore transformations, focusing specifically on translating triangles. These examples visually demonstrate how shapes move within a coordinate plane, reinforcing understanding of shifts along axes. Translation examples assist in grasping the basic concept of shifting figures without altering their orientation or shape. |
Applications of Transformations and Applications of Triangles |