
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 13: More Solutions to Linear Equations
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
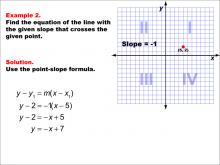
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 2 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 2TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of -1 passing through the point (5, 2). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - 2 = -(x - 5). After simplification, the final equation of the line is y = -x + 7. |
Point-Slope Form |
|
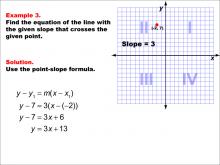
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 3 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 3TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of 3 passing through the point (-2, 7). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - 7 = 3(x - (-2)). After simplification, the resulting equation is y = 3x + 13. |
Point-Slope Form |
|
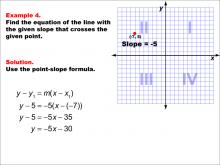
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of -5 that passes through the point (-7, 5). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - 5 = -5(x - (-7)). After simplification, the final equation of the line is y = -5x - 30. |
Point-Slope Form |
|
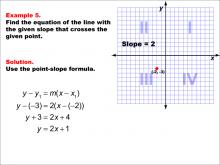
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of 2 passing through the point (-2, -3). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-3) = 2(x - (-2)). After simplification, the resulting equation is y = 2x + 1. |
Point-Slope Form |
|
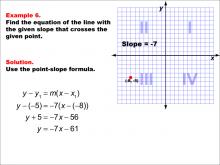
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -7 passing through the point (-8, -5). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-5) = -7(x - (-8)). After simplification, the resulting equation is y = -7x - 61. |
Point-Slope Form |
|
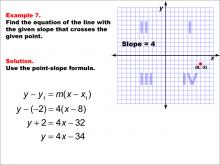
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of 4 passing through the point (8, -2). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - (-2) = 4(x - 8). After simplification, the final equation of the line is y = 4x - 34. |
Point-Slope Form |
|
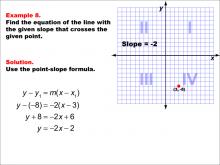
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -2 passing through the point (3, -8). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-8) = -2(x - 3). After simplification, the resulting equation is y = -2x - 2. |
Point-Slope Form |
|
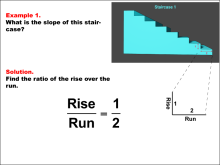
Math Example: The Slope As Rise Over Run: Three Examples | In this set of math examples, see how slope is calculated for a staircase based on measures for the rise and the run. |
Slope |

|
MATH EXAMPLES--Teacher's Guide: Finding the Equation of a Line, Given Two Points | MATH EXAMPLES--Teacher's Guide: Finding the Equation of a Line, Given Two Points
This Teacher's Guide provides an overview of the 12 worked-out examples that show how to find the equation of a line, given two points. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Linear Functions and Graphs of Linear Functions |

|
MATH EXAMPLES--Teacher's Guide: Graphs of Linear Functions in Slope-Intercept Form | MATH EXAMPLES--Teacher's Guide: Graphs of Linear Functions in Slope-Intercept Form
This Teacher's Guide provides an overview of the 13 worked-out examples that show how to graph a linear function, given the slope and y-intercept. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Linear Functions and Graphs of Linear Functions |

|
MATH EXAMPLES--Teacher's Guide: The Midpoint Formula | MATH EXAMPLES--Teacher's Guide: The Midpoint Formula
This Teacher's Guide provides an overview of the 20 worked-out examples that show how to use the Midpont Formula. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Midpoint Formula |

|
MATH EXAMPLES--Teacher's Guide: The Point Slope Form | MATH EXAMPLES--Teacher's Guide: The Point Slope Form
This Teacher's Guide provides an overview of the 8 worked-out examples that show how to find the equation of a lineusing the Point Slope Form. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Linear Functions and Graphs of Linear Functions |

|
MATH EXAMPLES--Teacher's Guide: The Slope Formula | MATH EXAMPLES--Teacher's Guide: The Slope Formula
This Teacher's Guide provides an overview of the 21 worked-out examples that show how to use the Slope Formula. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Linear Functions and Slope |

|
MATH EXAMPLES--The Slope Formula | MATH EXAMPLES--The Slope Formula
The complete set of 21 examples that make up this set of tutorials. NOTE: The download is a PPT file. |
Applications of Linear Functions and Slope |

|
Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Easy) | Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Easy)
This is part of a collection of math quizzes on the topic of finding the Equation of a Line Given Two Points. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Point-Slope Form and Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Hard) | Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Hard)
This is part of a collection of math quizzes on the topic of finding the Equation of a Line Given Two Points. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Point-Slope Form and Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Medium) | Paper-and-Pencil Quiz: Equation of a Line Given Two Points (Medium)
This is part of a collection of math quizzes on the topic of finding the Equation of a Line Given Two Points. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Point-Slope Form and Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Linear Equations Given m and b (Easy) | Paper-and-Pencil Quiz: Linear Equations Given m and b (Easy)
This is part of a collection of math quizzes on the topic of Linear Equations. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Linear Equations Given m and b (Hard) | Paper-and-Pencil Quiz: Linear Equations Given m and b (Hard)
This is part of a collection of math quizzes on the topic of Linear Equations. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Linear Equations Given m and b (Medium) | Paper-and-Pencil Quiz: Linear Equations Given m and b (Medium)
This is part of a collection of math quizzes on the topic of Linear Equations. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope-Intercept Form |

|
Paper-and-Pencil Quiz: Slope Formula (Easy) | Paper-and-Pencil Quiz: Slope Formula (Easy)
This is part of a collection of math quizzes on the topic of the Slope Formula. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope |

|
Paper-and-Pencil Quiz: Slope Formula (Hard) | Paper-and-Pencil Quiz: Slope Formula (Hard)
This is part of a collection of math quizzes on the topic of the Slope Formula. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope |

|
Paper-and-Pencil Quiz: Slope Formula (Medium) | Paper-and-Pencil Quiz: Slope Formula (Medium)
This is part of a collection of math quizzes on the topic of the Slope Formula. To see the complete quiz collection on this topic, click on this link. Note: The download is the PDF version of the quiz (with answer key).Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Quiz LibraryTo see the complete collection of Quizzes, click on this link.ary">click on this link. |
Slope |

|
Promethean Flipchart: Algebra Jeopardy | In this Promethean Flipchart, review key concepts from linear functions using a Jeopardy-style game. Note: The download for this resources is the Promethean Flipchart. | Applications of Equations and Inequalities |

|
Promethean Flipchart: Algebra Nspirations: Systems of Equations | Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video introduces students to systems of linear equations in two or three unknowns. To solve these systems, the host illustrates a variety of methods: four involve the TI-Nspire (spreadsheet, graphs and geometry, matrices and nSolve) and two are the classic algebraic methods known as substitution and elimination, also called the linear combinations method. The video ends with a summary of the three possible types of solutions. Concepts explored: equations, linear equations, linear systems Note: The download for this resources is the Promethean Flipchart. To access the full video [Algebra Nspirations: Solving Systems of Equations]: https://media4math.com/library/algebra-nspirations-solving-systems-equations |
Applications of Linear Systems |

|
Quizlet Flash Cards: Non-linear Systems | Description In this set of Quizlet flash cards test understanding of nonlinear systems. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see other resources related to this topic, click on the Resources tab above. Quizlet LibraryTo see the complete Quizlet Flash Card Library, click on this Link to see the collection. |
Solving Systems of Equations |

|
Quizlet Flash Cards: Slope Formula, Set 01 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 02 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 03 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 04 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 05 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 06 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 07 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 08 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 09 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Slope Formula, Set 10 | Find the slope of the line connecting two points in this 20-flash card set. The integers are in the range -20 to 20. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete collection of Quizlet Flash Cards on this topic, click on this link: https://bit.ly/36XwrY6 |
Slope |

|
Quizlet Flash Cards: Solving Systems Using the Elimination Method | In this set of Quizlet flash cards test understanding of solving systems using the elimination method. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete Quizlet Flash Card Library, click on this link: https://media4math.com/Quizlet-Resources |
Solving Systems of Equations |

|
Quizlet Flash Cards: Solving Systems Using the Substitution Method | In this set of Quizlet flash cards test understanding of solving systems using the substitution method. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete Quizlet Flash Card Library, click on this link: https://media4math.com/Quizlet-Resources |
Solving Systems of Equations |

|
Quizlet Flash Cards: Systems of Linear Equations | In this set of Quizlet flash cards test understanding of linear systems. Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards. Related ResourcesTo see the complete Quizlet Flash Card Library, click on this link: https://media4math.com/Quizlet-Resources |
Solving Systems of Equations |
|
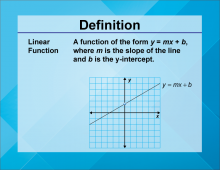
Video Definition 1--Linear Function Concepts--Linear Function | Video Definition 1--Linear Function Concepts--Linear Function
TopicLinear Functions DescriptionThe term is "Linear Function," defined as a function of the form y = mx + b, where m is the slope of the line and b is the y-intercept. This term provides the basic definition of linear functions, integral to understanding their behavior and applications. |
Slope-Intercept Form |
|
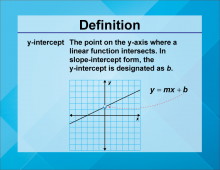
Video Definition 10--Linear Function Concepts--y-Intercept | Video Definition 10--Linear Function Concepts--y-Intercept
TopicLinear Functions DescriptionThe term is "y-Intercept," defined as the point on the y-axis where a linear function intersects. In slope-intercept form, it is designated as b in y = mx + b. This term complements the x-intercept by focusing on the vertical axis, completing the understanding of graph interactions. |
Slope-Intercept Form |
|
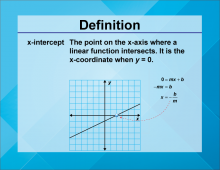
Video Definition 11--Linear Function Concepts--x-Intercept | Video Definition 11--Linear Function Concepts--x-Intercept
TopicLinear Functions DescriptionThe term is "x-Intercept," defined as the point on the x-axis where a linear function intersects, calculated as x = -b/m when y = 0 in the equation y = mx + b. This term provides insight into the graphical representation of linear functions and their interaction with the x-axis. |
Slope-Intercept Form |
|
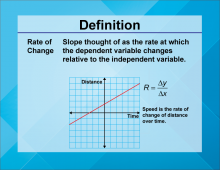
Video Definition 12--Linear Function Concepts--Rate of Change | Video Definition 12--Linear Function Concepts--Rate of Change
TopicLinear Functions DescriptionThe term is "Rate of Change," defined as the slope, interpreted as the rate at which the dependent variable changes relative to the independent variable. An example is speed as a rate of change of distance over time. This term highlights the application of slope in real-world scenarios, making the concept more tangible and relatable. |
Slope |

|
Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines | Video Definition 13--Linear Function Concepts--Equations of Perpendicular Lines
TopicLinear Functions DescriptionThe term is "Equations of Perpendicular Lines," defined as two linear functions with graphs that are perpendicular. Their slopes are negative reciprocals, represented as y1 = mx + b1 and y2 = -1/m * x + b2. This term explores the relationship between slopes of perpendicular lines, deepening understanding of linear graph orientations. |
Slope-Intercept Form |

|
Video Definition 14--Linear Function Concepts--Equations of Parallel Lines | Video Definition 14--Linear Function Concepts--Equations of Parallel Lines
TopicLinear Functions DescriptionThe term is "Equations of Parallel Lines," defined as two linear functions with parallel graphs that have the same slope but different y-intercepts. Represented as y1 = mx + b1 and y2 = mx + b2, where m is the slope. This term explains the geometric relationship of parallel lines, reinforcing the role of slope in linear functions. |
Slope-Intercept Form |

|
Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form | Video Definition 15--Linear Function Concepts--Linear Equations in Standard Form
TopicLinear Functions DescriptionThe term is "Linear Equation in Standard Form," defined as a linear equation with two variables and three constant terms, represented as Ax + By = C where A and B are not equal to zero. This term sets the stage for converting between forms of linear equations, essential for solving and graphing. |
Standard Form |

|
Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form | Video Definition 16--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form
TopicLinear Functions DescriptionThe term is "Converting from Standard Form to Slope-Intercept Form," defined as rewriting a linear equation in the form y = mx + b using the constants from the standard form Ax + By = C. The conversion formula is y = -A/B * x + C/B. This term is crucial for transitioning between different representations of linear equations, enabling easier analysis and graphing. |
Slope-Intercept Form |
|
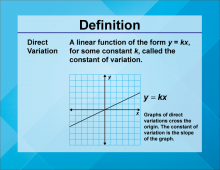
Video Definition 17--Linear Function Concepts--Direct Variation | Video Definition 17--Linear Function Concepts--Direct Variation
TopicLinear Functions DescriptionThe term is "Direct Variation," defined as a linear function of the form y = kx, where k is the constant of variation. Graphs of direct variations cross the origin, and the constant of variation is the slope of the graph. This term emphasizes proportional relationships in linear functions, highlighting their simplicity and graphical characteristics. |
Slope-Intercept Form |
|
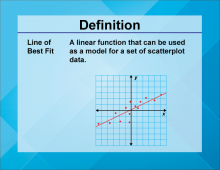
Video Definition 18--Linear Function Concepts--Line of Best Fit | Video Definition 18--Linear Function Concepts--Line of Best Fit
TopicLinear Functions DescriptionThe term is "Line of Best Fit," defined as a linear function that serves as a model for a set of scatterplot data. It helps represent the central trend of data points. This term enhances understanding of linear functions in the context of data analysis and graphical trends. |
Graphs of Linear Functions |
|
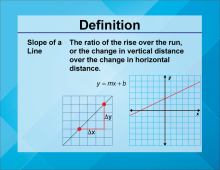
Video Definition 19--Linear Function Concepts--Slope | Video Definition 19--Linear Function Concepts--Slope
TopicLinear Functions DescriptionThe term is "Slope of a Line," defined as the ratio of the rise over the run, or the change in vertical distance over the change in horizontal distance. Represented as m in the equation y = mx + b. This term is a fundamental component of linear equations, providing a measure of steepness and direction. |
Slope |