
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 5: Introduction to Linear Relationships
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
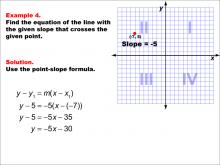
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of -5 that passes through the point (-7, 5). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - 5 = -5(x - (-7)). After simplification, the final equation of the line is y = -5x - 30. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of -5 that passes through the point (-7, 5). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - 5 = -5(x - (-7)). After simplification, the final equation of the line is y = -5x - 30. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of -5 that passes through the point (-7, 5). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - 5 = -5(x - (-7)). After simplification, the final equation of the line is y = -5x - 30. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of -5 that passes through the point (-7, 5). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - 5 = -5(x - (-7)). After simplification, the final equation of the line is y = -5x - 30. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 4TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of -5 that passes through the point (-7, 5). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - 5 = -5(x - (-7)). After simplification, the final equation of the line is y = -5x - 30. |
Point-Slope Form |
|
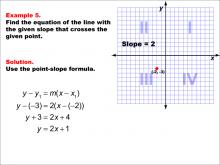
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of 2 passing through the point (-2, -3). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-3) = 2(x - (-2)). After simplification, the resulting equation is y = 2x + 1. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of 2 passing through the point (-2, -3). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-3) = 2(x - (-2)). After simplification, the resulting equation is y = 2x + 1. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of 2 passing through the point (-2, -3). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-3) = 2(x - (-2)). After simplification, the resulting equation is y = 2x + 1. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of 2 passing through the point (-2, -3). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-3) = 2(x - (-2)). After simplification, the resulting equation is y = 2x + 1. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of 2 passing through the point (-2, -3). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-3) = 2(x - (-2)). After simplification, the resulting equation is y = 2x + 1. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 5TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of 2 passing through the point (-2, -3). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-3) = 2(x - (-2)). After simplification, the resulting equation is y = 2x + 1. |
Point-Slope Form |
|
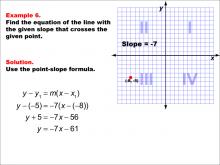
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -7 passing through the point (-8, -5). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-5) = -7(x - (-8)). After simplification, the resulting equation is y = -7x - 61. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -7 passing through the point (-8, -5). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-5) = -7(x - (-8)). After simplification, the resulting equation is y = -7x - 61. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -7 passing through the point (-8, -5). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-5) = -7(x - (-8)). After simplification, the resulting equation is y = -7x - 61. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -7 passing through the point (-8, -5). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-5) = -7(x - (-8)). After simplification, the resulting equation is y = -7x - 61. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -7 passing through the point (-8, -5). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-5) = -7(x - (-8)). After simplification, the resulting equation is y = -7x - 61. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 6TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -7 passing through the point (-8, -5). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-5) = -7(x - (-8)). After simplification, the resulting equation is y = -7x - 61. |
Point-Slope Form |
|
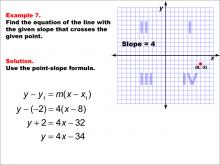
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of 4 passing through the point (8, -2). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - (-2) = 4(x - 8). After simplification, the final equation of the line is y = 4x - 34. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of 4 passing through the point (8, -2). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - (-2) = 4(x - 8). After simplification, the final equation of the line is y = 4x - 34. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of 4 passing through the point (8, -2). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - (-2) = 4(x - 8). After simplification, the final equation of the line is y = 4x - 34. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of 4 passing through the point (8, -2). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - (-2) = 4(x - 8). After simplification, the final equation of the line is y = 4x - 34. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of 4 passing through the point (8, -2). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - (-2) = 4(x - 8). After simplification, the final equation of the line is y = 4x - 34. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 7TopicThe Point-Slope Form DescriptionIn this example, we explore finding the equation of a line with a slope of 4 passing through the point (8, -2). Applying the point-slope formula y - y1 = m(x - x1), we substitute the given values to obtain y - (-2) = 4(x - 8). After simplification, the final equation of the line is y = 4x - 34. |
Point-Slope Form |
|
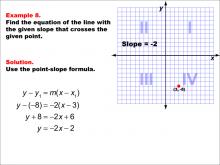
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -2 passing through the point (3, -8). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-8) = -2(x - 3). After simplification, the resulting equation is y = -2x - 2. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -2 passing through the point (3, -8). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-8) = -2(x - 3). After simplification, the resulting equation is y = -2x - 2. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -2 passing through the point (3, -8). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-8) = -2(x - 3). After simplification, the resulting equation is y = -2x - 2. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -2 passing through the point (3, -8). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-8) = -2(x - 3). After simplification, the resulting equation is y = -2x - 2. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -2 passing through the point (3, -8). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-8) = -2(x - 3). After simplification, the resulting equation is y = -2x - 2. |
Point-Slope Form |

|
Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8 | Math Example--Linear Function Concepts--The Point-Slope Formula: Example 8TopicThe Point-Slope Form DescriptionThis example demonstrates the application of the point-slope formula to find the equation of a line with a slope of -2 passing through the point (3, -8). Using the formula y - y1 = m(x - x1), we substitute the given values to get y - (-8) = -2(x - 3). After simplification, the resulting equation is y = -2x - 2. |
Point-Slope Form |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1TopicRatios, Proportions, and Percents DescriptionThis example demonstrates how to solve a proportion problem where two ratios a:b and c:d are proportional. Given the values b = 3, c = 4, and d = 6, we need to find the value of a. The proportion is set up as a / 3 = 4 / 6, which is then solved to find that a = 2. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 1TopicRatios, Proportions, and Percents DescriptionThis example demonstrates how to solve a proportion problem where two ratios a:b and c:d are proportional. Given the values b = 3, c = 4, and d = 6, we need to find the value of a. The proportion is set up as a / 3 = 4 / 6, which is then solved to find that a = 2. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar triangles with algebraic expressions. Two triangles are shown, one with sides of 6 and 9, and the other with sides of 2x and 2x + 9. The problem requires setting up a proportion: 6 / 9 = 2x / (2x + 9). Solving this equation leads to x = 9, which then allows us to find the side lengths of 18 and 27. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 10TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar triangles with algebraic expressions. Two triangles are shown, one with sides of 6 and 9, and the other with sides of 2x and 2x + 9. The problem requires setting up a proportion: 6 / 9 = 2x / (2x + 9). Solving this equation leads to x = 9, which then allows us to find the side lengths of 18 and 27. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, one with legs of 7 and 9, and the other with legs of 14 and x. The problem requires finding the length of side x by setting up a proportion based on the similar triangles: 7 / 9 = 14 / x. Solving this equation leads to x = 18. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 11TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, one with legs of 7 and 9, and the other with legs of 14 and x. The problem requires finding the length of side x by setting up a proportion based on the similar triangles: 7 / 9 = 14 / x. Solving this equation leads to x = 18. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, one with legs of 5 and 8, and the other with legs of 2x and (2x + 6). The problem requires setting up a proportion: 5 / 8 = 2x / (2x + 6). Solving this equation leads to x = 5, which then allows us to find the side lengths of 10 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 12TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, one with legs of 5 and 8, and the other with legs of 2x and (2x + 6). The problem requires setting up a proportion: 5 / 8 = 2x / (2x + 6). Solving this equation leads to x = 5, which then allows us to find the side lengths of 10 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°). Two triangles are shown, with the smaller one having sides of 6√3 and 6, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: (6√3) / 6 = x / 12. Solving this equation leads to x = 12√3. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 13TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°). Two triangles are shown, with the smaller one having sides of 6√3 and 6, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: (6√3) / 6 = x / 12. Solving this equation leads to x = 12√3. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°) and algebraic expressions. Two triangles are shown, with the smaller one having sides of 16 and 8, and the larger one having sides of (3x + 4) and 2x. The problem requires setting up a proportion: 16 / 8 = (3x + 4) / 2x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 8 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 14TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with special angles (30°-60°-90°) and algebraic expressions. Two triangles are shown, with the smaller one having sides of 16 and 8, and the larger one having sides of (3x + 4) and 2x. The problem requires setting up a proportion: 16 / 8 = (3x + 4) / 2x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 8 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the smaller one having sides of 4 and 3, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: 4 / 3 = x / 12. Solving this equation leads to x = 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 15TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the smaller one having sides of 4 and 3, and the larger one having sides of x and 12. The problem requires finding the length of side x by setting up a proportion: 4 / 3 = x / 12. Solving this equation leads to x = 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the smaller one having sides of (3x + 4) and 6, and the larger one having sides of 3x and 3x. The problem requires setting up a proportion: 8 / 6 = (3x + 4) / 3x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 12 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 16TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the smaller one having sides of (3x + 4) and 6, and the larger one having sides of 3x and 3x. The problem requires setting up a proportion: 8 / 6 = (3x + 4) / 3x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 12 and 16. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 12 / 5 = x / 15. Solving this equation leads to x = 36. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 17TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar right triangles. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of x and 15. The problem requires finding the length of side x by setting up a proportion: 12 / 5 = x / 15. Solving this equation leads to x = 36. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of 10x + 8 and 5x. The problem requires setting up a proportion: 12 / 5 = (10x + 8) / 5x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 20 and 48. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 18TopicRatios, Proportions, and Percents DescriptionThis example illustrates solving a proportion problem using similar right triangles with algebraic expressions. Two right triangles are shown, with the left one having sides of 12 and 5, and the right one having sides of 10x + 8 and 5x. The problem requires setting up a proportion: 12 / 5 = (10x + 8) / 5x. Solving this equation leads to x = 4, which then allows us to find the side lengths of 20 and 48. |
Proportions |

|
Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 19 | Math Example--Ratios, Proportions, and Percents--Solving Proportions: Example 19TopicRatios, Proportions, and Percents DescriptionThis example demonstrates solving a proportion problem using similar isosceles right triangles. Two 45-45-90 triangles are shown, with one having sides labeled y and 5√2, and the other having sides labeled x and 12. The problem requires finding the lengths of both x and y using the special properties of isosceles right triangles and proportions. |
Proportions |