
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 7: Representations of Linear Relationships
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant IV | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant IVTopicSlope DescriptionDemonstrates calculating a negative slope in Quadrant IV. Example points are (9, -3) and (3, -1), with a slope of -1/3. Discusses coordinate differences and formula application. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant IV | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant IVTopicSlope DescriptionDemonstrates calculating a negative slope in Quadrant IV. Example points are (9, -3) and (3, -1), with a slope of -1/3. Discusses coordinate differences and formula application. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant IV | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant IVTopicSlope DescriptionDemonstrates calculating a negative slope in Quadrant IV. Example points are (9, -3) and (3, -1), with a slope of -1/3. Discusses coordinate differences and formula application. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant IV | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrant IVTopicSlope DescriptionDemonstrates calculating a negative slope in Quadrant IV. Example points are (9, -3) and (3, -1), with a slope of -1/3. Discusses coordinate differences and formula application. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants I and II | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants I and IITopicSlope DescriptionThe video discusses a negative slope with points in Quadrants I and II. Using (4, 2) and (-2, 8), it calculates a slope of -1. Highlights include rise over run and coordinate simplifications. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants I and II | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants I and IITopicSlope DescriptionThe video discusses a negative slope with points in Quadrants I and II. Using (4, 2) and (-2, 8), it calculates a slope of -1. Highlights include rise over run and coordinate simplifications. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants I and II | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants I and IITopicSlope DescriptionThe video discusses a negative slope with points in Quadrants I and II. Using (4, 2) and (-2, 8), it calculates a slope of -1. Highlights include rise over run and coordinate simplifications. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants I and II | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants I and IITopicSlope DescriptionThe video discusses a negative slope with points in Quadrants I and II. Using (4, 2) and (-2, 8), it calculates a slope of -1. Highlights include rise over run and coordinate simplifications. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants III and IV | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants III and IVTopicSlope DescriptionExplains calculating a negative slope for points in Quadrants III and IV. Example points (7, -5) and (-5, -1) yield a slope of -1/3. Key topics include applying the slope formula and simplifying results. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants III and IV | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants III and IVTopicSlope DescriptionExplains calculating a negative slope for points in Quadrants III and IV. Example points (7, -5) and (-5, -1) yield a slope of -1/3. Key topics include applying the slope formula and simplifying results. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants III and IV | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants III and IVTopicSlope DescriptionExplains calculating a negative slope for points in Quadrants III and IV. Example points (7, -5) and (-5, -1) yield a slope of -1/3. Key topics include applying the slope formula and simplifying results. |
Slope |

|
Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants III and IV | Closed Captioned Video: Slope Formula: Negative Slope, Coordinates in Quadrants III and IVTopicSlope DescriptionExplains calculating a negative slope for points in Quadrants III and IV. Example points (7, -5) and (-5, -1) yield a slope of -1/3. Key topics include applying the slope formula and simplifying results. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant I | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant ITopicSlope DescriptionThis video explains the slope formula and applies it to find the positive slope of a line in Quadrant I. Key concepts include rise over run and calculating differences in coordinates. The example uses points (2, 3) and (6, 7) with the slope calculated as 1. Vocabulary includes rise, run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant I | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant ITopicSlope DescriptionThis video explains the slope formula and applies it to find the positive slope of a line in Quadrant I. Key concepts include rise over run and calculating differences in coordinates. The example uses points (2, 3) and (6, 7) with the slope calculated as 1. Vocabulary includes rise, run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant I | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant ITopicSlope DescriptionThis video explains the slope formula and applies it to find the positive slope of a line in Quadrant I. Key concepts include rise over run and calculating differences in coordinates. The example uses points (2, 3) and (6, 7) with the slope calculated as 1. Vocabulary includes rise, run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant I | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant ITopicSlope DescriptionThis video explains the slope formula and applies it to find the positive slope of a line in Quadrant I. Key concepts include rise over run and calculating differences in coordinates. The example uses points (2, 3) and (6, 7) with the slope calculated as 1. Vocabulary includes rise, run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant II | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IITopicSlope DescriptionThis tutorial focuses on a positive slope in Quadrant II. Key topics include calculating slope as rise over run and using coordinate differences. It provides an example with points (-5, 4) and (-3, 8) resulting in a slope of 2. Vocabulary includes numerator, denominator, and difference. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant II | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IITopicSlope DescriptionThis tutorial focuses on a positive slope in Quadrant II. Key topics include calculating slope as rise over run and using coordinate differences. It provides an example with points (-5, 4) and (-3, 8) resulting in a slope of 2. Vocabulary includes numerator, denominator, and difference. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant II | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IITopicSlope DescriptionThis tutorial focuses on a positive slope in Quadrant II. Key topics include calculating slope as rise over run and using coordinate differences. It provides an example with points (-5, 4) and (-3, 8) resulting in a slope of 2. Vocabulary includes numerator, denominator, and difference. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant II | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IITopicSlope DescriptionThis tutorial focuses on a positive slope in Quadrant II. Key topics include calculating slope as rise over run and using coordinate differences. It provides an example with points (-5, 4) and (-3, 8) resulting in a slope of 2. Vocabulary includes numerator, denominator, and difference. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant III | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IIITopicSlope DescriptionShows how to calculate a positive slope in Quadrant III using the slope formula. Example uses points (-3, -8) and (-2, -2), with a slope of 6. Concepts include rise over run and simplifying fractions. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant III | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IIITopicSlope DescriptionShows how to calculate a positive slope in Quadrant III using the slope formula. Example uses points (-3, -8) and (-2, -2), with a slope of 6. Concepts include rise over run and simplifying fractions. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant III | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IIITopicSlope DescriptionShows how to calculate a positive slope in Quadrant III using the slope formula. Example uses points (-3, -8) and (-2, -2), with a slope of 6. Concepts include rise over run and simplifying fractions. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant III | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IIITopicSlope DescriptionShows how to calculate a positive slope in Quadrant III using the slope formula. Example uses points (-3, -8) and (-2, -2), with a slope of 6. Concepts include rise over run and simplifying fractions. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IV | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IVTopicSlope DescriptionExplains finding a positive slope in Quadrant IV. Demonstrates using points (2, -5) and (4, -1) to calculate a slope of 2. Vocabulary includes rise over run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IV | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IVTopicSlope DescriptionExplains finding a positive slope in Quadrant IV. Demonstrates using points (2, -5) and (4, -1) to calculate a slope of 2. Vocabulary includes rise over run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IV | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IVTopicSlope DescriptionExplains finding a positive slope in Quadrant IV. Demonstrates using points (2, -5) and (4, -1) to calculate a slope of 2. Vocabulary includes rise over run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IV | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrant IVTopicSlope DescriptionExplains finding a positive slope in Quadrant IV. Demonstrates using points (2, -5) and (4, -1) to calculate a slope of 2. Vocabulary includes rise over run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants I and II | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants I and IITopicSlope DescriptionCovers a positive slope with points spanning Quadrants I and II. Example uses (-3, 3) and (3, 6), yielding a slope of 1/2. Discusses rise over run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants I and II | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants I and IITopicSlope DescriptionCovers a positive slope with points spanning Quadrants I and II. Example uses (-3, 3) and (3, 6), yielding a slope of 1/2. Discusses rise over run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants I and II | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants I and IITopicSlope DescriptionCovers a positive slope with points spanning Quadrants I and II. Example uses (-3, 3) and (3, 6), yielding a slope of 1/2. Discusses rise over run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants I and II | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants I and IITopicSlope DescriptionCovers a positive slope with points spanning Quadrants I and II. Example uses (-3, 3) and (3, 6), yielding a slope of 1/2. Discusses rise over run, numerator, and denominator. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants III and IV | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants III and IVTopicSlope DescriptionThis video demonstrates finding a positive slope with points in Quadrants III and IV. Using points (-5, -9) and (3, -5), it calculates a slope of 1/2. Concepts covered include rise over run and simplifying coordinate differences. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants III and IV | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants III and IVTopicSlope DescriptionThis video demonstrates finding a positive slope with points in Quadrants III and IV. Using points (-5, -9) and (3, -5), it calculates a slope of 1/2. Concepts covered include rise over run and simplifying coordinate differences. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants III and IV | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants III and IVTopicSlope DescriptionThis video demonstrates finding a positive slope with points in Quadrants III and IV. Using points (-5, -9) and (3, -5), it calculates a slope of 1/2. Concepts covered include rise over run and simplifying coordinate differences. |
Slope |

|
Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants III and IV | Closed Captioned Video: Slope Formula: Positive Slope, Coordinates in Quadrants III and IVTopicSlope DescriptionThis video demonstrates finding a positive slope with points in Quadrants III and IV. Using points (-5, -9) and (3, -5), it calculates a slope of 1/2. Concepts covered include rise over run and simplifying coordinate differences. |
Slope |

|
Definition--Direct Variation | Direct Variation
TopicLinear Functions DefinitionDirect variation describes a linear relationship between two variables where one variable is a constant multiple of the other, expressed as y = kx, where k is the constant of variation. DescriptionDirect variation is a fundamental concept in linear functions, illustrating how one variable changes proportionally with another. The constant of variation, 𝑘 k, represents the rate of change. In real-world scenarios, direct variation can model relationships such as speed and distance, where distance traveled varies directly with time at a constant speed. Understanding this concept is crucial in fields like physics and engineering. |
Applications of Linear Functions |

|
Definition--Direct Variation | Direct Variation
TopicLinear Functions DefinitionDirect variation describes a linear relationship between two variables where one variable is a constant multiple of the other, expressed as y = kx, where k is the constant of variation. DescriptionDirect variation is a fundamental concept in linear functions, illustrating how one variable changes proportionally with another. The constant of variation, 𝑘 k, represents the rate of change. In real-world scenarios, direct variation can model relationships such as speed and distance, where distance traveled varies directly with time at a constant speed. Understanding this concept is crucial in fields like physics and engineering. |
Applications of Linear Functions |

|
Definition--Direct Variation | Direct Variation
TopicLinear Functions DefinitionDirect variation describes a linear relationship between two variables where one variable is a constant multiple of the other, expressed as y = kx, where k is the constant of variation. DescriptionDirect variation is a fundamental concept in linear functions, illustrating how one variable changes proportionally with another. The constant of variation, 𝑘 k, represents the rate of change. In real-world scenarios, direct variation can model relationships such as speed and distance, where distance traveled varies directly with time at a constant speed. Understanding this concept is crucial in fields like physics and engineering. |
Applications of Linear Functions |

|
Definition--Slope Concepts--Delta x | Delta xTopicSlope DefinitionDelta x is the change in the x-coordinate in a linear relationship. DescriptionThe term Delta x is fundamental to understanding slope as it represents the horizontal change in a line’s position. In real-world applications, Delta x can represent the distance traveled over time in physics and engineering contexts. |
Slope |

|
Definition--Slope Concepts--Delta x | Delta xTopicSlope DefinitionDelta x is the change in the x-coordinate in a linear relationship. DescriptionThe term Delta x is fundamental to understanding slope as it represents the horizontal change in a line’s position. In real-world applications, Delta x can represent the distance traveled over time in physics and engineering contexts. |
Slope |

|
Definition--Slope Concepts--Delta x | Delta xTopicSlope DefinitionDelta x is the change in the x-coordinate in a linear relationship. DescriptionThe term Delta x is fundamental to understanding slope as it represents the horizontal change in a line’s position. In real-world applications, Delta x can represent the distance traveled over time in physics and engineering contexts. |
Slope |

|
Definition--Slope Concepts--Delta y | Delta yTopicSlope DefinitionDelta y is the change in the y-coordinate in a linear relationship. DescriptionThe term Delta y signifies the vertical change, essential for calculating slope used in graphing and data interpretation. In practical scenarios, Delta y can illustrate changes in temperature over time or the rise in elevation in geography. |
Slope |

|
Definition--Slope Concepts--Delta y | Delta yTopicSlope DefinitionDelta y is the change in the y-coordinate in a linear relationship. DescriptionThe term Delta y signifies the vertical change, essential for calculating slope used in graphing and data interpretation. In practical scenarios, Delta y can illustrate changes in temperature over time or the rise in elevation in geography. |
Slope |

|
Definition--Slope Concepts--Delta y | Delta yTopicSlope DefinitionDelta y is the change in the y-coordinate in a linear relationship. DescriptionThe term Delta y signifies the vertical change, essential for calculating slope used in graphing and data interpretation. In practical scenarios, Delta y can illustrate changes in temperature over time or the rise in elevation in geography. |
Slope |
|
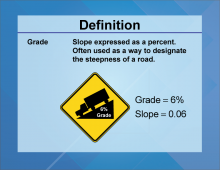
Definition--Slope Concepts--Grade | GradeTopicSlope DefinitionGrade is a ratio indicating the steepness of a slope. DescriptionThe term Grade commonly refers to the angle of elevation or slope expressed as a percentage. In engineering, grades are crucial for designing roads and railways, ensuring safety and efficiency. |
Slope |

|
Definition--Slope Concepts--Grade | GradeTopicSlope DefinitionGrade is a ratio indicating the steepness of a slope. DescriptionThe term Grade commonly refers to the angle of elevation or slope expressed as a percentage. In engineering, grades are crucial for designing roads and railways, ensuring safety and efficiency. |
Slope |

|
Definition--Slope Concepts--Grade | GradeTopicSlope DefinitionGrade is a ratio indicating the steepness of a slope. DescriptionThe term Grade commonly refers to the angle of elevation or slope expressed as a percentage. In engineering, grades are crucial for designing roads and railways, ensuring safety and efficiency. |
Slope |
|
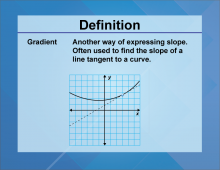
Definition--Slope Concepts--Gradient | GradientTopicSlope DefinitionGradient represents the rate of change of a quantity. DescriptionThe Gradient measures how steep a line is, calculated by the ratio of the rise to run. This concept is significant in fields like physics and economics where gradients can represent relationships between variables. |
Slope |

|
Definition--Slope Concepts--Gradient | GradientTopicSlope DefinitionGradient represents the rate of change of a quantity. DescriptionThe Gradient measures how steep a line is, calculated by the ratio of the rise to run. This concept is significant in fields like physics and economics where gradients can represent relationships between variables. |
Slope |