
Illustrative Math Alignment: Grade 8 Unit 3
Linear Relationships
Lesson 7: Representations of Linear Relationships
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|
|
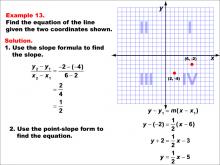
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 13 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 13TopicLinear Functions DescriptionThis image shows a graph with two points (2, -4) and (6, -2) marked. The example demonstrates how to find the equation of a line passing through these points. The slope is calculated as 1/2, and the point-slope form is used to derive the equation of the line. The slope formula is used: (y2 - y1) / (x2 - x1) = (-2 - (-4)) / (6 - 2) = 2 / 4 = 1/2. Then, using the point-slope form: y - (-2) = (1/2)(x - 6), which simplifies to y = (1/2)x - 5. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 13 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 13TopicLinear Functions DescriptionThis image shows a graph with two points (2, -4) and (6, -2) marked. The example demonstrates how to find the equation of a line passing through these points. The slope is calculated as 1/2, and the point-slope form is used to derive the equation of the line. The slope formula is used: (y2 - y1) / (x2 - x1) = (-2 - (-4)) / (6 - 2) = 2 / 4 = 1/2. Then, using the point-slope form: y - (-2) = (1/2)(x - 6), which simplifies to y = (1/2)x - 5. |
Point-Slope Form and Slope-Intercept Form |
|
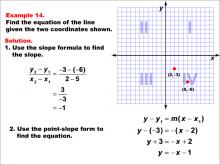
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 14 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 14TopicLinear Functions DescriptionThis image shows a graph with two points (2, -3) and (5, -6). The example demonstrates how to find the equation of a line passing through these points. The slope is calculated as -1, and the point-slope form is used to derive the equation. The slope formula is used: (y2 - y1) / (x2 - x1) = (-3 - (-6)) / (2 - 5) = 3 / -3 = -1. Then, using the point-slope form: y - (-3) = -(x - 2), which simplifies to y = -x - 1. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 14 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 14TopicLinear Functions DescriptionThis image shows a graph with two points (2, -3) and (5, -6). The example demonstrates how to find the equation of a line passing through these points. The slope is calculated as -1, and the point-slope form is used to derive the equation. The slope formula is used: (y2 - y1) / (x2 - x1) = (-3 - (-6)) / (2 - 5) = 3 / -3 = -1. Then, using the point-slope form: y - (-3) = -(x - 2), which simplifies to y = -x - 1. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 14 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 14TopicLinear Functions DescriptionThis image shows a graph with two points (2, -3) and (5, -6). The example demonstrates how to find the equation of a line passing through these points. The slope is calculated as -1, and the point-slope form is used to derive the equation. The slope formula is used: (y2 - y1) / (x2 - x1) = (-3 - (-6)) / (2 - 5) = 3 / -3 = -1. Then, using the point-slope form: y - (-3) = -(x - 2), which simplifies to y = -x - 1. |
Point-Slope Form and Slope-Intercept Form |
|
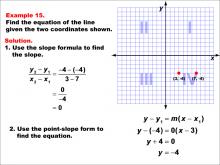
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 15 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 15TopicLinear Functions DescriptionThis image shows a graph with two points (3, -4) and (7, -4). The example demonstrates how to find the equation of a horizontal line passing through these points. The slope is calculated as 0, and the point-slope form is used to derive the equation. The slope formula is used: (y2 - y1) / (x2 - x1) = (-4 - (-4)) / (7 - 3) = 0 / 4 = 0. Then, using the point-slope form: y - (-4) = 0(x - 3), which simplifies to y = -4. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 15 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 15TopicLinear Functions DescriptionThis image shows a graph with two points (3, -4) and (7, -4). The example demonstrates how to find the equation of a horizontal line passing through these points. The slope is calculated as 0, and the point-slope form is used to derive the equation. The slope formula is used: (y2 - y1) / (x2 - x1) = (-4 - (-4)) / (7 - 3) = 0 / 4 = 0. Then, using the point-slope form: y - (-4) = 0(x - 3), which simplifies to y = -4. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 15 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 15TopicLinear Functions DescriptionThis image shows a graph with two points (3, -4) and (7, -4). The example demonstrates how to find the equation of a horizontal line passing through these points. The slope is calculated as 0, and the point-slope form is used to derive the equation. The slope formula is used: (y2 - y1) / (x2 - x1) = (-4 - (-4)) / (7 - 3) = 0 / 4 = 0. Then, using the point-slope form: y - (-4) = 0(x - 3), which simplifies to y = -4. |
Point-Slope Form and Slope-Intercept Form |
|
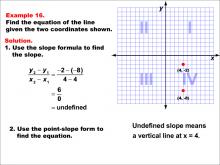
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 16 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 16TopicLinear Functions DescriptionThis image shows a graph with two points (4, -8) and (4, -2). The example demonstrates how to find the equation of a vertical line passing through these points. The slope is undefined because division by zero occurs in calculating it. The slope formula is used: (y2 - y1) / (x2 - x1) = (-2 - (-8)) / (4 - 4) = 6 / 0 = undefined. Since this represents a vertical line, its equation is simply x = 4. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 16 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 16TopicLinear Functions DescriptionThis image shows a graph with two points (4, -8) and (4, -2). The example demonstrates how to find the equation of a vertical line passing through these points. The slope is undefined because division by zero occurs in calculating it. The slope formula is used: (y2 - y1) / (x2 - x1) = (-2 - (-8)) / (4 - 4) = 6 / 0 = undefined. Since this represents a vertical line, its equation is simply x = 4. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 16 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 16TopicLinear Functions DescriptionThis image shows a graph with two points (4, -8) and (4, -2). The example demonstrates how to find the equation of a vertical line passing through these points. The slope is undefined because division by zero occurs in calculating it. The slope formula is used: (y2 - y1) / (x2 - x1) = (-2 - (-8)) / (4 - 4) = 6 / 0 = undefined. Since this represents a vertical line, its equation is simply x = 4. |
Point-Slope Form and Slope-Intercept Form |
|
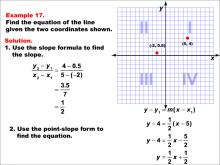
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-2, 0.5) and (5, 4). The example demonstrates how to find the equation of a line using the slope formula and point-slope form. The slope is calculated as (4 - 0.5) / (5 - (-2)) = 3.5 / 7 = 1 / 2. The point-slope form is used to find the equation: y - 4 = (1 / 2)(x - 5), resulting in y = (1 / 2)x + 1 / 2. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-2, 0.5) and (5, 4). The example demonstrates how to find the equation of a line using the slope formula and point-slope form. The slope is calculated as (4 - 0.5) / (5 - (-2)) = 3.5 / 7 = 1 / 2. The point-slope form is used to find the equation: y - 4 = (1 / 2)(x - 5), resulting in y = (1 / 2)x + 1 / 2. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 17TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-2, 0.5) and (5, 4). The example demonstrates how to find the equation of a line using the slope formula and point-slope form. The slope is calculated as (4 - 0.5) / (5 - (-2)) = 3.5 / 7 = 1 / 2. The point-slope form is used to find the equation: y - 4 = (1 / 2)(x - 5), resulting in y = (1 / 2)x + 1 / 2. |
Point-Slope Form and Slope-Intercept Form |
|
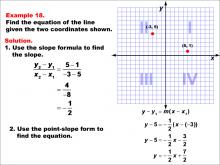
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 18 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 18TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-3, 5) and (5, 1). The example demonstrates how to find the equation of a line using the slope formula and point-slope form. The slope is calculated as (5 - 1) / (-3 - 5) = -1 / 2. The point-slope form is used to find the equation: y - 5 = (-1 / 2)(x + 3), resulting in y = (-1 / 2)x + 7 / 2. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 18 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 18TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-3, 5) and (5, 1). The example demonstrates how to find the equation of a line using the slope formula and point-slope form. The slope is calculated as (5 - 1) / (-3 - 5) = -1 / 2. The point-slope form is used to find the equation: y - 5 = (-1 / 2)(x + 3), resulting in y = (-1 / 2)x + 7 / 2. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 18 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 18TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-3, 5) and (5, 1). The example demonstrates how to find the equation of a line using the slope formula and point-slope form. The slope is calculated as (5 - 1) / (-3 - 5) = -1 / 2. The point-slope form is used to find the equation: y - 5 = (-1 / 2)(x + 3), resulting in y = (-1 / 2)x + 7 / 2. |
Point-Slope Form and Slope-Intercept Form |
|
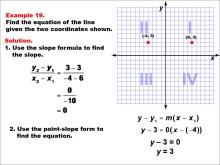
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 19 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 19TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-4, 3) and (6, 3). The example demonstrates how to find the equation of a horizontal line using the slope formula and point-slope form. The slope is calculated as (3 - 3) / (-4 - 6) = 0. Since the slope is zero, the equation of the line is simply y = 3, indicating a horizontal line passing through y = 3. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 19 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 19TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-4, 3) and (6, 3). The example demonstrates how to find the equation of a horizontal line using the slope formula and point-slope form. The slope is calculated as (3 - 3) / (-4 - 6) = 0. Since the slope is zero, the equation of the line is simply y = 3, indicating a horizontal line passing through y = 3. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 19 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 19TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-4, 3) and (6, 3). The example demonstrates how to find the equation of a horizontal line using the slope formula and point-slope form. The slope is calculated as (3 - 3) / (-4 - 6) = 0. Since the slope is zero, the equation of the line is simply y = 3, indicating a horizontal line passing through y = 3. |
Point-Slope Form and Slope-Intercept Form |
|
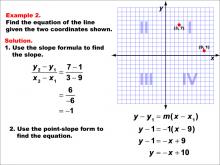
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 2 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 2TopicLinear Functions DescriptionThis example illustrates the process of finding the equation of a line passing through the points (3, 7) and (9, 1). The slope is calculated as -1 using the formula (y2 - y1) / (x2 - x1). Employing the point-slope form, y - y1 = m(x - x1), the equation is derived as y - 1 = -(x - 9), which simplifies to y = -x + 10. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 2 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 2TopicLinear Functions DescriptionThis example illustrates the process of finding the equation of a line passing through the points (3, 7) and (9, 1). The slope is calculated as -1 using the formula (y2 - y1) / (x2 - x1). Employing the point-slope form, y - y1 = m(x - x1), the equation is derived as y - 1 = -(x - 9), which simplifies to y = -x + 10. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 2 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 2TopicLinear Functions DescriptionThis example illustrates the process of finding the equation of a line passing through the points (3, 7) and (9, 1). The slope is calculated as -1 using the formula (y2 - y1) / (x2 - x1). Employing the point-slope form, y - y1 = m(x - x1), the equation is derived as y - 1 = -(x - 9), which simplifies to y = -x + 10. |
Point-Slope Form and Slope-Intercept Form |
|
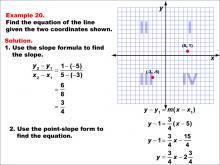
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-3, -5) and (5, 1). The example demonstrates how to find the equation of a line using the slope formula and point-slope form. The slope is calculated as (1 - (-5)) / (5 - (-3)) = 6 / 8 = 3 / 4. The point-slope form is used to find the equation: y - 1 = (3 / 4)(x - 5), resulting in y = 3/4x - 2 3/4. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-3, -5) and (5, 1). The example demonstrates how to find the equation of a line using the slope formula and point-slope form. The slope is calculated as (1 - (-5)) / (5 - (-3)) = 6 / 8 = 3 / 4. The point-slope form is used to find the equation: y - 1 = (3 / 4)(x - 5), resulting in y = 3/4x - 2 3/4. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 20TopicLinear Functions DescriptionThis image shows a graph with two points plotted at (-3, -5) and (5, 1). The example demonstrates how to find the equation of a line using the slope formula and point-slope form. The slope is calculated as (1 - (-5)) / (5 - (-3)) = 6 / 8 = 3 / 4. The point-slope form is used to find the equation: y - 1 = (3 / 4)(x - 5), resulting in y = 3/4x - 2 3/4. |
Point-Slope Form and Slope-Intercept Form |
|
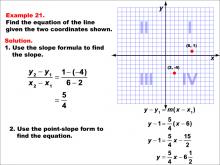
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21TopicLinear Functions DescriptionThe image shows a graph with two points (2, -4) and (6, 1) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-4)) / (6 - 2) = 5 / 4. Using point-slope form: y - 1 = (5 / 4)(x - 6), which simplifies to y = 5/4x - 6 1/2. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21TopicLinear Functions DescriptionThe image shows a graph with two points (2, -4) and (6, 1) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-4)) / (6 - 2) = 5 / 4. Using point-slope form: y - 1 = (5 / 4)(x - 6), which simplifies to y = 5/4x - 6 1/2. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 21TopicLinear Functions DescriptionThe image shows a graph with two points (2, -4) and (6, 1) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-4)) / (6 - 2) = 5 / 4. Using point-slope form: y - 1 = (5 / 4)(x - 6), which simplifies to y = 5/4x - 6 1/2. |
Point-Slope Form and Slope-Intercept Form |
|
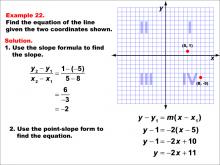
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22TopicLinear Functions DescriptionThe image shows a graph with two points (5, 1) and (8, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-5)) / (5 - 8) = -2. Using point-slope form: y - 1 = -2(x - 5), which simplifies to y = -2x + 11. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22TopicLinear Functions DescriptionThe image shows a graph with two points (5, 1) and (8, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-5)) / (5 - 8) = -2. Using point-slope form: y - 1 = -2(x - 5), which simplifies to y = -2x + 11. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 22TopicLinear Functions DescriptionThe image shows a graph with two points (5, 1) and (8, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (1 - (-5)) / (5 - 8) = -2. Using point-slope form: y - 1 = -2(x - 5), which simplifies to y = -2x + 11. |
Point-Slope Form and Slope-Intercept Form |
|
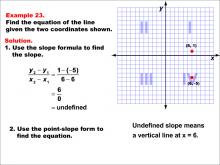
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23TopicLinear Functions DescriptionThe image shows a graph with two points (6, 1) and (6, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a vertical line using these two points. Since both x-coordinates are equal, the slope is undefined, indicating a vertical line. The slope is undefined because x-values are equal: (1 - (-5)) / (6 - 6) = undefined. This means it's a vertical line at x = 6. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23TopicLinear Functions DescriptionThe image shows a graph with two points (6, 1) and (6, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a vertical line using these two points. Since both x-coordinates are equal, the slope is undefined, indicating a vertical line. The slope is undefined because x-values are equal: (1 - (-5)) / (6 - 6) = undefined. This means it's a vertical line at x = 6. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 23TopicLinear Functions DescriptionThe image shows a graph with two points (6, 1) and (6, -5) marked on a coordinate plane. The example demonstrates how to find the equation of a vertical line using these two points. Since both x-coordinates are equal, the slope is undefined, indicating a vertical line. The slope is undefined because x-values are equal: (1 - (-5)) / (6 - 6) = undefined. This means it's a vertical line at x = 6. |
Point-Slope Form and Slope-Intercept Form |
|
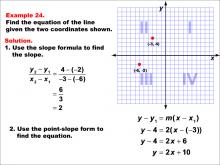
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24TopicLinear Functions DescriptionThe image shows a graph with two points (-6, -2) and (-3, 4) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (4 - (-2)) / (-3 - (-6)) = 2. Using point-slope form: y - 4 = 2(x + 3), which simplifies to y = 2x + 10. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24TopicLinear Functions DescriptionThe image shows a graph with two points (-6, -2) and (-3, 4) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (4 - (-2)) / (-3 - (-6)) = 2. Using point-slope form: y - 4 = 2(x + 3), which simplifies to y = 2x + 10. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 24TopicLinear Functions DescriptionThe image shows a graph with two points (-6, -2) and (-3, 4) marked on a coordinate plane. The example demonstrates how to find the equation of a line using these two points. The slope is calculated using the slope formula, and then the point-slope form is applied to derive the equation of the line. The slope is calculated as (4 - (-2)) / (-3 - (-6)) = 2. Using point-slope form: y - 4 = 2(x + 3), which simplifies to y = 2x + 10. |
Point-Slope Form and Slope-Intercept Form |
|
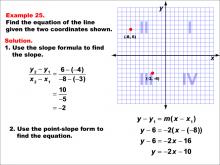
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25TopicLinear Functions DescriptionA graph with two points (-8, 6) and (-3, -4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -2x - 10. The slope is calculated as (-4 - 6) / (-3 - (-8)) = -2. Using the point-slope form y - y1 = m(x - x1), the equation becomes y - 6 = -2(x + 8), which simplifies to y = -2x - 10. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25TopicLinear Functions DescriptionA graph with two points (-8, 6) and (-3, -4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -2x - 10. The slope is calculated as (-4 - 6) / (-3 - (-8)) = -2. Using the point-slope form y - y1 = m(x - x1), the equation becomes y - 6 = -2(x + 8), which simplifies to y = -2x - 10. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 25TopicLinear Functions DescriptionA graph with two points (-8, 6) and (-3, -4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -2x - 10. The slope is calculated as (-4 - 6) / (-3 - (-8)) = -2. Using the point-slope form y - y1 = m(x - x1), the equation becomes y - 6 = -2(x + 8), which simplifies to y = -2x - 10. |
Point-Slope Form and Slope-Intercept Form |
|
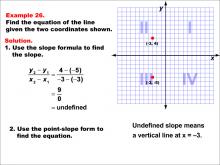
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26TopicLinear Functions DescriptionA graph with two points (-8, -6) and (4, 2) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = 1/4 x - 3. The slope is calculated as (2 + 6) / (4 + 8) = 1/4. Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 2 = 1/4(x - 4), which simplifies to y = 1/4 x - 3. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26TopicLinear Functions DescriptionA graph with two points (-8, -6) and (4, 2) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = 1/4 x - 3. The slope is calculated as (2 + 6) / (4 + 8) = 1/4. Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 2 = 1/4(x - 4), which simplifies to y = 1/4 x - 3. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 26TopicLinear Functions DescriptionA graph with two points (-8, -6) and (4, 2) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = 1/4 x - 3. The slope is calculated as (2 + 6) / (4 + 8) = 1/4. Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 2 = 1/4(x - 4), which simplifies to y = 1/4 x - 3. |
Point-Slope Form and Slope-Intercept Form |
|
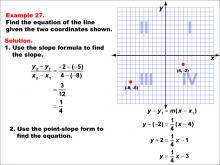
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27TopicLinear Functions DescriptionA graph with two points (-3, 4) and (-3, -5) marked on a coordinate plane. The slope is undefined because both x-coordinates are equal, leading to division by zero. This represents a vertical line at x = -3. The slope is undefined because (4 + 5) / (-3 + 3) results in division by zero. This indicates a vertical line at x = -3. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27TopicLinear Functions DescriptionA graph with two points (-3, 4) and (-3, -5) marked on a coordinate plane. The slope is undefined because both x-coordinates are equal, leading to division by zero. This represents a vertical line at x = -3. The slope is undefined because (4 + 5) / (-3 + 3) results in division by zero. This indicates a vertical line at x = -3. |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 27TopicLinear Functions DescriptionA graph with two points (-3, 4) and (-3, -5) marked on a coordinate plane. The slope is undefined because both x-coordinates are equal, leading to division by zero. This represents a vertical line at x = -3. The slope is undefined because (4 + 5) / (-3 + 3) results in division by zero. This indicates a vertical line at x = -3. |
Point-Slope Form and Slope-Intercept Form |
|
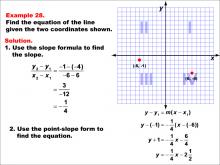
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28TopicLinear Functions DescriptionA graph with two points (-6, -1) and (6, 4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -(1/4)x - 2.5 or -(1/4)x - (5/2). The slope is calculated as (4 + 1) / (6 + 6) = -(1/4). Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 1 = -(1/4)(x + 6), which simplifies to y = -(1/4)x - (5/2). |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28TopicLinear Functions DescriptionA graph with two points (-6, -1) and (6, 4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -(1/4)x - 2.5 or -(1/4)x - (5/2). The slope is calculated as (4 + 1) / (6 + 6) = -(1/4). Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 1 = -(1/4)(x + 6), which simplifies to y = -(1/4)x - (5/2). |
Point-Slope Form and Slope-Intercept Form |

|
Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28 | Math Example--Linear Function Concepts--The Equation of a Line Given Two Points: Example 28TopicLinear Functions DescriptionA graph with two points (-6, -1) and (6, 4) marked on a coordinate plane. The slope is calculated using the formula (y2 - y1) / (x2 - x1), and the equation of the line is derived using the point-slope form. The final equation is y = -(1/4)x - 2.5 or -(1/4)x - (5/2). The slope is calculated as (4 + 1) / (6 + 6) = -(1/4). Using the point-slope form y - y1 = m(x - x1), the equation becomes y + 1 = -(1/4)(x + 6), which simplifies to y = -(1/4)x - (5/2). |
Point-Slope Form and Slope-Intercept Form |