
Illustrative Math Alignment: Grade 8 Unit 3
Functions and Volume
Lesson 14: Finding Cylinder Dimensions
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Holiday Themed Resource Collection: Math in the News |
This is a collection of Holiday-Themed issues of Math in the News.
|
Data Analysis, Applications of Exponential and Logarithmic Functions, Surface Area and Volume |

|
Lesson Plan Collection: Cross-Sections of 3D Figures | Cross-Sections of 3D Figures | 3-Lesson Unit This collection of geometry lesson plans explores how slicing three-dimensional figures produces different cross-sections. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Math in the News Collection: Applications of Surface Area and Volume |
OverviewThis is a collection of issues of Math in the News that deal with applications of Surface Area and Volume.
|
Surface Area and Volume |

|
Math in the News Collection: Applications of 3D Geometry |
OverviewThis is a collection of issues of Math in the News that deal with applications of 3D geometry.
|
3-Dimensional Figures and Applications of 3D Geometry |

|
Math in the News Collection: Business Math |
OverviewThis is a collection of issues of Math in the News that deal with business applications.
|
Applications of Exponential and Logarithmic Functions, Data Analysis and Volume |

|
Math in the News Collection: Applications of Data Analysis |
OverviewThis is a collection of Math in the News stories that focus on the topic of Data Analysis.
|
Data Analysis, Data Gathering, Probability, Percents and Ratios and Rates |

|
Math Video Collection: 3D Geometry Animations |
OverviewThis collection aggregates all the math videos and resources in this series: 3D Geometry Animations. There are a total of 10 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.
|
3-Dimensional Figures, Cubes, Cones, Triangular Prisms, Pyramids, Cylinders and Rectangular Prisms |

|
Math Video Collection: Geometry Applications Video Series: 3D Geometry | OverviewThis collection aggregates all the math videos and resources in this series: Geometry Applications Video Series: 3D Geometry. There are a total of 18 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.
|
3-Dimensional Figures, Applications of 3D Geometry, Pyramids, Cylinders, Rectangular Prisms and Triangular Prisms |
|
Math Examples Collection: Volume | OverviewThis collection of math examples on the topic of Volume provides students with an in-depth exploration of volume concepts through a variety of visual models. Covering a range of skills and increasing in complexity, this collection helps students master foundational and advanced topics in volume. From calculating the volume of basic geometric shapes to applying volume formulas to complex objects, these examples build confidence and enhance comprehension by breaking down challenging concepts visually. |
Volume |

|
VIDEO: 3D Geometry Animation: Antiprism | VIDEO: 3D Geometry Animation: Antiprism
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Triangular Prisms |

|
VIDEO: 3D Geometry Animation: Cone | VIDEO: 3D Geometry Animation: Cone
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Cones |

|
VIDEO: 3D Geometry Animation: Cube | VIDEO: 3D Geometry Animation: Cube
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Cubes |

|
VIDEO: 3D Geometry Animation: Cylinder | 3D Geometry Animation: Cylinder
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Cylinders |

|
VIDEO: 3D Geometry Animation: Octahedron | VIDEO: 3D Geometry Animation: Octahedron
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures |

|
VIDEO: 3D Geometry Animation: Pyramid | VIDEO: 3D Geometry Animation: Pyramid
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Pyramids |

|
VIDEO: 3D Geometry Animation: Rectangular Prism | VIDEO: 3D Geometry Animation: Rectangular Prism
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures and Rectangular Prisms |

|
VIDEO: 3D Geometry Animation: Tetrahedron | VIDEO: 3D Geometry Animation: Tetrahedron
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures |

|
VIDEO: 3D Geometry Animation: Triangular Prism | VIDEO: 3D Geometry Animation: Triangular Prism
This is part of a series of video animations of three-dimensional figures. These animations show different views of these figures: top, side, and bottom. Many of these figures are a standard part of the geometry curriculum and being able to recognize them is important. — CLICK THE PREVIEW BUTTON TO SEE THE VIDEO ANIMATION —Study these animations to learn the basic properties of these 3D figures. In particular, make a note of their sides, edges, and vertices. Look for any symmetries they have. Look for polygon shapes that are familiar. Finally, think of real-world examples that use these figures. Below we also include information about Platonic solids and 2D nets of these 3D figures. To get a better understanding of these 3D figures, study these basic forms. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Cube with Horizontal Cross-Section | Cube with Horizontal Cross-SectionTopic3D Geometry DescriptionThis animation shows a cube with a horizontal cross-section, illustrating how slicing the cube parallel to its base results in a square cross-section. This is useful for visualizing and understanding the internal structure and symmetry of cubes. Using animated math clip art like this helps students visualize the concept of cross-sections and their applications in geometry. Teachers can use this image to explain how horizontal cross-sections reveal the internal structure of cubes. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Dodecahedron | DodecahedronTopic3D Geometry DescriptionA dodecahedron is a three-dimensional shape with twelve flat faces, each a regular pentagon. This animated clip art shows the rotation of a dodecahedron, highlighting its symmetry and geometric properties. Animated math clip art like this is crucial for teaching as it allows students to visualize complex polyhedra, enhancing their understanding of geometric concepts. Teachers can use this image to explain the structure and characteristics of dodecahedrons. Here is a potential script for teachers: "Today, we are going to explore the geometry of a dodecahedron. Notice how the twelve pentagonal faces form a symmetrical shape. This helps us understand the properties of polyhedra." |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Horizontal Cross-Section of a Rectangular Prism | Animated Math Clip Art: Horizontal Cross-Section of a Rectangular Prism This animated math clip art illustrates how a horizontal plane intersects a rectangular prism, forming a two-dimensional cross-section. As the plane moves through the prism, students can observe that the resulting cross-section is always a rectangle, reinforcing key geometric concepts related to slicing three-dimensional shapes. Ideal for classroom instruction, this GIF animation helps students develop spatial reasoning by demonstrating how horizontal slices interact with the structure of a rectangular prism. This visual aid is particularly useful for teaching cross-sections in geometry, emphasizing how different slicing directions produce distinct 2D shapes. |
Rectangular Prisms |

|
Animated Math Clip Art--3D Geometry--Rotating a Rectangle to Form a Cylinder | Rotating a Rectangle to Form a CylinderTopic3D Geometry DescriptionThis animation demonstrates how rotating a rectangle around one of its sides creates a cylinder. It's a powerful visualization of how 2D shapes can generate 3D objects through rotation. Using animated math clip art like this helps students understand the concept of solids of revolution. Teachers can use this to introduce topics in calculus, such as finding volumes using the disk or washer methods. |
Cylinders |
|
Animated Math Clip Art--3D Geometry--Rotating a Rectangle to Form an Open Cylinder | Rotating a Rectangle to Form an Open CylinderTopic3D Geometry DescriptionThis animation shows how rotating a rectangular strip around an axis parallel to one of its sides creates an open cylinder. It illustrates the concept of surface area of revolution. Animated math clip art like this is valuable for teaching as it helps students visualize how 2D shapes can generate 3D surfaces. Teachers can use this to introduce topics in calculus, such as finding surface areas of revolution. |
Cylinders |

|
Animated Math Clip Art--3D Geometry--Rotating a Square to Form a Cylinder | Rotating a Square to Form a CylinderTopic3D Geometry DescriptionThis animation demonstrates how rotating a square around one of its sides creates a cylinder. It's a special case of rotating a rectangle, where the height and diameter of the resulting cylinder are equal. Using animated math clip art like this helps students understand the relationship between 2D and 3D shapes. Teachers can use this to discuss how the dimensions of the original shape relate to the dimensions of the resulting solid. |
Cylinders |

|
Animated Math Clip Art--3D Geometry--Vertical Cross-Section of a Rectangular Prism | Animated Math Clip Art: Vertical Cross-Section of a Rectangular Prism This animated math clip art visually demonstrates how a vertical plane intersects a rectangular prism, producing a two-dimensional cross-section. As the plane moves through the 3D shape, students can observe how the resulting cross-section remains a rectangle, reinforcing key geometric concepts related to slicing three-dimensional figures. Perfect for classroom instruction, this GIF animation helps students develop spatial reasoning by illustrating how a vertical slice interacts with the faces of a rectangular prism. This resource is particularly useful for teaching cross-sections in geometry and preparing students to understand more complex 3D slicing concepts. |
Rectangular Prisms |

|
Closed Captioned Video: Geometry Applications: 3D Geometry | Closed Captioned Video: Geometry Applications: 3D GeometryTopic3D Geometry |
3-Dimensional Figures and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 1 | Closed Captioned Video: Geometry Applications: 3D Geometry, 1Topic3D Geometry DescriptionDescription: This segment introduces Platonic solids, including tetrahedron, cube, and dodecahedron, emphasizing their congruent edges, vertices, and angles. It connects these geometric figures to both natural and man-made structures, setting the stage for exploring 3D geometry applications. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 2 | Closed Captioned Video: Geometry Applications: 3D Geometry, 2Topic3D Geometry DescriptionDescription: This segment explores pyramids, particularly Mayan and Egyptian structures, to distinguish rectangular and square bases. It discusses the volume of truncated pyramids using proportional relationships and introduces the concept of tiered volume reduction through geometric sequences. |
3-Dimensional Figures, Pyramids and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 3 | Closed Captioned Video: Geometry Applications: 3D Geometry, 3Topic3D Geometry DescriptionDescription: This segment examines cylinders, using the Shanghai Tower as a case study. It highlights how adjustments to height and radius affect volume and surface area, demonstrating these principles with geometric calculations and their architectural applications in energy efficiency. |
3-Dimensional Figures, Cylinders and Applications of 3D Geometry |

|
Definition--3D Geometry Concepts--Cylinder | CylinderTopic3D Geometry DefinitionA cylinder is a three-dimensional geometric figure with two parallel circular bases connected by a curved surface at a fixed distance from each other. DescriptionIn the realm of three-dimensional geometry, a cylinder is a fundamental shape characterized by its two identical, parallel circular bases and a curved surface that connects these bases. The line segment joining the centers of the bases is called the axis of the cylinder, and it is perpendicular to the bases. The distance between the bases is the height of the cylinder, while the radius is the distance from the center to the edge of the base. |
Cylinders |
|
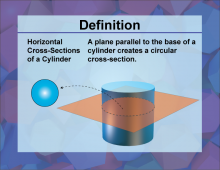
Definition--3D Geometry Concepts--Horizontal Cross-Sections of a Cylinder | Horizontal Cross Sections of a CylinderTopic3D Geometry DefinitionA horizontal cross-section of a cylinder is the intersection of the cylinder with a plane that is parallel to the base of the cylinder. DescriptionIn the context of three-dimensional geometry, understanding the concept of cross-sections is crucial. A cylinder is a three-dimensional shape with two parallel circular bases connected by a curved surface. When a horizontal plane intersects a cylinder, the resulting cross-section is a circle. This concept is not only fundamental in geometry but also has practical applications in various fields. |
Cylinders |
|
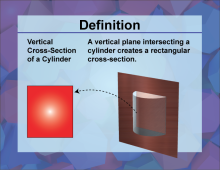
Definition--3D Geometry Concepts--Vertical Cross-Sections of a Cylinder | Vertical Cross Sections of a CylinderTopic3D Geometry DefinitionA vertical cross-section of a cylinder is the intersection of the cylinder with a plane that is parallel to its axis. This cross-section is typically a rectangle if the plane cuts through the entire height of the cylinder. |
Cylinders |

|
Formulas--Surface Area of a Cylinder | Formulas--Surface Area of a Cylinder
The formula for the Surface Area of a Cylinder. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Surface Area and Cylinders |

|
Formulas--Volume of a Cylinder | Formulas--Volume of a Cylinder
The formula for the Volume of a Cylinder. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume and Cylinders |

|
Geometry Applications Teachers Guide: 3D Geometry | Geometry Applications Teachers Guide: 3D Geometry
This is the Teacher's Guide that accompanies Geometry Applications: 3D Geometry. This is part of a collection of teacher's guides. To see the complete collection of teacher's guides, click on this link. Note: The download is a PDF file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of 3D Geometry |

|
Google Earth Voyager Story: Circular Structures, Part 2 | Google Earth Voyager Story: Circular Structures, Part 2TopicGeometric Models |
Applications of Circles and Cylinders |

|
INSTRUCTIONAL RESOURCE: Math Examples 55 | INSTRUCTIONAL RESOURCE: Math Examples--Surface Area
This set of tutorials provides an overview of the 24 worked-out examples that show how to calculate the surface area of different three-dimensional figures. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file.Library of Instructional ResourcesTo see the complete library of Instructional Resources , click on this link. |
Surface Area |

|
Lesson Plan: Cross-Sections of 3D Figures, Part 1 | Lesson Plan: Cross-Sections of 3D Figures In this engaging math lesson, students explore cross-sections of cubes, cylinders, and cones through interactive activities, real-world examples, and animated visuals. They will learn how slicing three-dimensional shapes in different ways produces a variety of two-dimensional figures, helping to develop spatial reasoning and geometric understanding. The lesson begins with a conceptual introduction to cross-sections, followed by hands-on practice with everyday objects such as gift boxes, paper towel rolls, and ice cream cones. Students will investigate how horizontal, vertical, and diagonal slices impact the resulting shapes. Animated GIFs illustrate these concepts, reinforcing learning through dynamic visual representations. |
3-Dimensional Figures |

|
Math Clip Art--3D Figures--Cylinder | Math Clip Art--3D Figures--Cylinder
This collection of clip art images includes images of 3D figures and composite figures. |
3-Dimensional Figures and Applications of 3D Geometry |
|
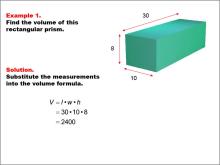
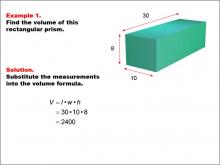
Math Example--Volume Concepts--Calculating Volume: Example 1 | Math Example--Volume Concepts--Calculating Volume: Example 1TopicVolume DescriptionA rectangular prism with dimensions labeled: length = 30, width = 10, and height = 8. The image shows how to find the volume of the prism using the formula for volume of a rectangular prism. This image illustrates Example 1: The caption explains how to calculate the volume of the rectangular prism using the formula V = l * w * h. The given dimensions are substituted into the formula: V = 30 * 10 * 8 = 2400.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 10 | Math Example--Volume Concepts--Calculating Volume: Example 10TopicVolume DescriptionA green cylinder with a general radius y and height x. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 10: The task is to find the volume of this cylinder. The volume formula V = πr2h is used, and substituting r = y and h = x, the volume is calculated as V = xy2π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 11 | Math Example--Volume Concepts--Calculating Volume: Example 11TopicVolume DescriptionA hollow green cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 11: The task is to find the volume of this hollow cylinder. The volume formula for a hollow cylinder V = πr12h1 - πr22h2 is used. Substituting values, the result is V = 285π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 12 | Math Example--Volume Concepts--Calculating Volume: Example 12TopicVolume DescriptionA hollow green cylinder with an outer radius y, an inner radius y - 1, and a height x. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 12: The task is to find the volume of this hollow cylinder. Using V = π(r12h1 - r22h2), substituting values gives: V = πx(y2 - (y - 1)2= πx(2y - 1). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 13 | Math Example--Volume Concepts--Calculating Volume: Example 13TopicVolume DescriptionA rectangular-based pyramid is shown with dimensions: base length 10, base width 8, and height 30. The image demonstrates how to calculate the volume of this pyramid. This image illustrates Example 13: The caption provides a step-by-step solution for calculating the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h. Substituting values: V = (1/3) * 8 * 10 * 30 = 800. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 14 | Math Example--Volume Concepts--Calculating Volume: Example 14TopicVolume DescriptionA general rectangular-based pyramid is shown with variables x, y, and z representing the base dimensions and height. This example shows how to calculate the volume of a pyramid using variables instead of specific numbers. This image illustrates Example 14: The caption explains how to calculate the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h, which simplifies to V = (1/3) * x * y * z. |
Volume |
|
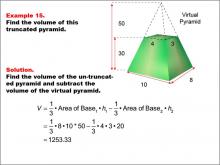
Math Example--Volume Concepts--Calculating Volume: Example 15 | Math Example--Volume Concepts--Calculating Volume: Example 15TopicVolume |
Volume |
|
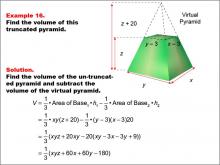
Math Example--Volume Concepts--Calculating Volume: Example 16 | Math Example--Volume Concepts--Calculating Volume: Example 16TopicVolume DescriptionA truncated rectangular-based pyramid is shown with variables x, y, and z representing dimensions. The smaller virtual pyramid has reduced dimensions by 3 units for both width and length and reduced height by z - 20. The image demonstrates how to calculate the volume in terms of variables. This image illustrates Example 16: The caption explains how to find the volume of a truncated pyramid using variables for both pyramids' dimensions. Formula: V = (1/3) * xy(z + 20) - (1/3) * (y - 3)(x - 3)(z), which simplifies to V = (1/3) * (xyz + 60x + 60y - 180). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 17 | Math Example--Volume Concepts--Calculating Volume: Example 17TopicVolume DescriptionA green sphere with a radius labeled as 3. The image is part of a math example showing how to calculate the volume of a sphere. This image illustrates Example 17: The text describes finding the volume of a sphere. The formula used is V = (4/3) * π * r3, where r = 3. After substituting, the result is V = 36π. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 18 | Math Example--Volume Concepts--Calculating Volume: Example 18TopicVolume Description
A green sphere with a radius labeled as x. This image is part of a math example showing how to calculate the volume of a sphere using an unknown radius. This image illustrates Example 18: The text explains how to find the volume of a sphere with an unknown radius x. The formula used is V = (4/3) * π * r3, and substituting r = x gives V = (4/3) * x3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 19 | Math Example--Volume Concepts--Calculating Volume: Example 19TopicVolume Description
A green cube with side length labeled as 7. The image illustrates how to calculate the volume of a cube with known side length. This image illustrates Example 19: The text describes finding the volume of a cube. The formula used is V = s3, where s = 7. After substituting, the result is V = 343. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |