Illustrative Math Alignment: Grade 8 Unit 8

Pythagorean Theorem and Irrational Numbers

Lesson 4: Square Roots on the Number Line

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topic
Linear Functions and Equations Collection: Video Tutorials	Overview This collection of videos analyzes linear functions in slope-intercept form. There are a total of 18 videos.	Graphs of Linear Functions, Standard Form, Point-Slope Form, Slope, Special Functions and Applications of Linear Functions
Quadratics Collection: Texas Instruments Graphing Calculator Resources	A set of resources for the TI-Nspire, TI-Nspire CX, and the Nspire App.	Applications of Quadratic Functions, Graphs of Quadratic Functions, Quadratic Formula, Data Analysis, Quadratic Equations and Functions, Inequalities and Composite Functions
Math Examples Collection: Quadratics	Overview This comprehensive collection of quadratic examples offers a valuable resource for students and educators alike. The examples cover a wide range of quadratic concepts, progressively increasing in complexity to challenge learners at various skill levels ls to simplify complex quadratic concepts, making them more accessible and easier to understand. These visual aids help students grasp abstract ideas and reinforce their understanding of quadratic functions, equations, and graphs	Quadratic Formula, Quadratic Equations and Functions, Conic Sections, Factoring Quadratics, Graphs of Quadratic Functions, The FOIL Method, Numerical and Algebraic Expressions and Polynomial Expressions
Halloween Math Collection	Overview This is a collection of Halloween-themed math clip art and other resources. There are more than 40 resources. To see the complete collection of Math Clip Art, click on this link.	3-Dimensional Figures, Applications of 3D Geometry, Numerical Expressions, Even and Odd Numbers, Ratios and Rates, Counting, Data Analysis and Divide by 1-Digit Numbers
Math in the News Collection: Applications of 3D Geometry	Overview This is a collection of issues of Math in the News that deal with applications of 3D geometry.	3-Dimensional Figures and Applications of 3D Geometry
Math Video Collection: Video Tutorials Series: Rational Numbers	Overview This collection aggregates all the math videos and resources in this series: Video Tutorials Series: Rational Numbers. There are a total of 39 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.	Rational Expressions
Math Examples Collection: Rational Approximations of Rational Numbers	Overview This collection aggregates all the math examples around the topic of Rational Approximations of Rational Numbers. There are a total of 10 Math Examples. This collection of resources is made up of downloadable PNG images that you can easily incorporate into your lesson plans.	Rational Expressions
Math Examples Collection: The Discriminant	Overview This collection aggregates all the math examples around the topic of Calculating the Discriminant. There are a total of 10 Math Examples. This collection of resources is made up of downloadable PNG images that you can easily incorporate into your lesson plans.	Quadratic Formula
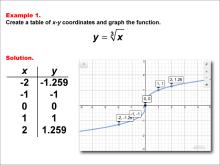
Math Examples Collection: Cube Root Functions in Tabular and Graph Form	Overview This comprehensive collection of 40 math examples focuses on Cube Root Functions, offering educators a wealth of resources to enhance their lesson plans. The examples are designed to progressively increase in complexity, covering a wide range of skills related to cube root functions. By utilizing visual models, these examples help simplify complex concepts, making them more accessible to students.	Polynomial Functions and Equations
Holiday Themed Resource Collection: Instructional Resources	This is a collection of Holiday-Themed math activities.	Ratios and Rates and Numerical and Algebraic Expressions
Closed Captioned Video: Rational Numbers: Rational Numbers and Irrational Numbers	Closed Captioned Video: Rational Numbers: Rational Numbers and Irrational Numbers This is part of a collection of video tutorials on the topic of Rational Numbers. This includes defining rational numbers, rational number operations, comparing and ordering rational numbers, and applications of rational numbers. —PRESS PREVIEW TO SEE THE VIDEO TUTORIAL— To see the complete collection of these videos on fractions, click on this link. The following section includes background information on rational numbers. Refer to this section as you view the videos, or as review material afterward.	Rational Expressions
INSTRUCTIONAL RESOURCE: Algebra Application: Accident Investigation	INSTRUCTIONAL RESOURCE: Algebra Application: Accident Investigation In this Algebra Application, students develop a quadratic mathematical model for calculating the speed of a car based on the length of its skid marks. Using this model, students investigate the corresponding parabola. The math topics covered include: Mathematical modeling, Quadratic functions in standard form, Square root formula, Data analysis. The culminating activity is for students to write a program, using either a spreadsheet or a computer language like Python, that can calculate the speed of a car, given the skid mark length and coefficient of friction as the two inputs.	Applications of Quadratic Functions and Quadratic Equations and Functions
INSTRUCTIONAL RESOURCE: Math Examples 2	INSTRUCTIONAL RESOURCE: Math Examples--Completing the Square The complete set of 4 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Quadratic Formula and Quadratic Equations and Functions
INSTRUCTIONAL RESOURCE: Math Examples 40	INSTRUCTIONAL RESOURCE: Math Examples--Quadratic Formula The complete set of 12 examples that make up this set of tutorials. This is part of a collection of math examples for a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Quadratic Equations and Functions and Quadratic Formula
INSTRUCTIONAL RESOURCE: Nspire App Tutorial: Quadratic Formula Template	In this Slide Show, learn how to program a function for solving quadratic equations. This presentation requires the use of the TI-Nspire iPad App. Note: the download is a PPT.	Quadratic Formula
INSTRUCTIONAL RESOURCE: Pumpkin PI	In this Slide Show, do a hands-on geometry activity to measure π. Note: The download is a PPT file.	Ratios and Rates
INSTRUCTIONAL RESOURCE: Tutorial: Solving Quadratic Equations by Completing the Square	INSTRUCTIONAL RESOURCE: Tutorial: Solving Quadratic Equations by Completing the Square In this Slide Show, learn how to solve a quadratic equation by completing the square. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. < Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Quadratic Formula and Quadratic Equations and Functions
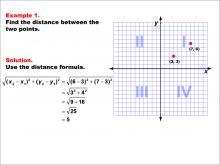
Math Example--Coordinate Geometry--Distance Formula: Example 1	Math Example--Coordinate Geometry--Distance Formula: Example 1 Topic Geometry Description This example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (3, 3) and (7, 6) are plotted on a graph, and the distance between them is calculated using the formula: √((6 - 3)2 + (7 - 3)2) = 5.	The Distance Formula
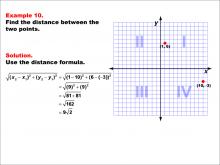
Math Example--Coordinate Geometry--Distance Formula: Example 10	Math Example--Coordinate Geometry--Distance Formula: Example 10 Topic Geometry Description This example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (1, 6) and (10, -3) are plotted on a graph, and the distance between them is determined using the formula: √((1 - 10)2 + (6 - (-3))2) = √(9^2 + 9^2) = √162 = 9√2.	The Distance Formula
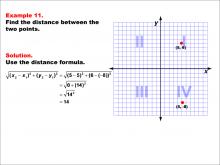
Math Example--Coordinate Geometry--Distance Formula: Example 11	Math Example--Coordinate Geometry--Distance Formula: Example 11 Topic Geometry Description This example demonstrates the application of the distance formula to find the vertical distance between two points on a coordinate plane. The points (5, 6) and (5, -8) are plotted on a graph, and the distance between them is calculated using the formula: √((5 - 5)2 + (6 - (-8))2) = √(0 + (14)2) = 14.	The Distance Formula
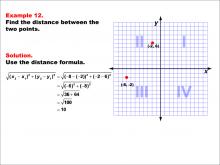
Math Example--Coordinate Geometry--Distance Formula: Example 12	Math Example--Coordinate Geometry--Distance Formula: Example 12 Topic Geometry Description This example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-8, -2) and (-2, 6) are plotted on a graph, and the distance between them is determined using the formula: √((-8 - (-2))2 + (-2 - 6)2) = √((-6)2 + (-8)2) = 10.	The Distance Formula
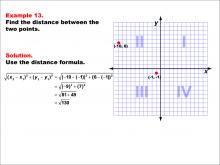
Math Example--Coordinate Geometry--Distance Formula: Example 13	Math Example--Coordinate Geometry--Distance Formula: Example 13 Topic Geometry Description This example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-10, 6) and (-1, -1) are plotted on a graph, and the distance between them is calculated using the formula: √((-10 - (-1))2 + (6 - (-1))2) = √((-9)2 + 72) = √130.	The Distance Formula
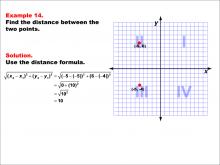
Math Example--Coordinate Geometry--Distance Formula: Example 14	Math Example--Coordinate Geometry--Distance Formula: Example 14 Topic Geometry Description This example illustrates the use of the distance formula to calculate the vertical distance between two points on a coordinate plane. The points (-5, 6) and (-5, -4) are plotted on a graph, and the distance between them is determined using the formula: √((-5 - (-5))2 + (6 - (-4))2) = √(0 + 102) = 10.	The Distance Formula
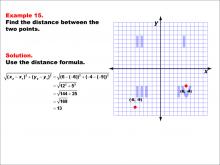
Math Example--Coordinate Geometry--Distance Formula: Example 15	Math Example--Coordinate Geometry--Distance Formula: Example 15 Topic Geometry Description This example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-6, -9) and (6, -4) are plotted on a graph, and the distance between them is calculated using the formula: √((6 - (-6))2 + (-4 - (-9))2) = √(122 + 52) = 13.	The Distance Formula
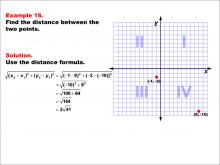
Math Example--Coordinate Geometry--Distance Formula: Example 16	Math Example--Coordinate Geometry--Distance Formula: Example 16 Topic Geometry Description This example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-1, -2) and (9, -10) are plotted on a graph, and the distance between them is determined using the formula: √((-1 - 9)2 + (-2 - (-10))2) = √((-10)2 + 82) = 2√41.	The Distance Formula
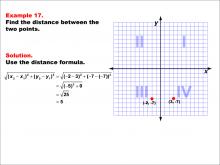
Math Example--Coordinate Geometry--Distance Formula: Example 17	Math Example--Coordinate Geometry--Distance Formula: Example 17 Topic Geometry Description This example demonstrates the application of the distance formula to find the horizontal distance between two points on a coordinate plane. The points (-2, -7) and (3, -7) are plotted on a graph, and the distance between them is calculated using the formula: √((-2 - 3)2 + (-7 + 7)2) = √((-5)2 + 0) = 5.	The Distance Formula
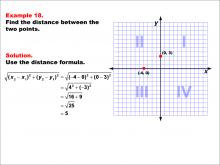
Math Example--Coordinate Geometry--Distance Formula: Example 18	Math Example--Coordinate Geometry--Distance Formula: Example 18 Topic Geometry Description This example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-4, 0) and (0, 3) are plotted on a graph, and the distance between them is determined using the formula: √((4 - 0)2 + (0 - 3)2) = √(16 + 9) = 5.	The Distance Formula
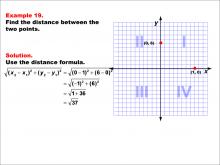
Math Example--Coordinate Geometry--Distance Formula: Example 19	Math Example--Coordinate Geometry--Distance Formula: Example 19 Topic Geometry Description This example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (0, 6) and (1, 0) are plotted on a graph, and the distance between them is calculated using the formula: √((0 - 1)2 + (6 - 0)2) = √(1 + 36) = √37.	The Distance Formula
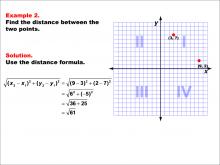
Math Example--Coordinate Geometry--Distance Formula: Example 2	Math Example--Coordinate Geometry--Distance Formula: Example 2 Topic Geometry Description This example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (3, 7) and (9, 2) are plotted on a graph, and the distance between them is determined using the formula: √((9 - 3)2 + (2 - 7)2) = √(61).	The Distance Formula
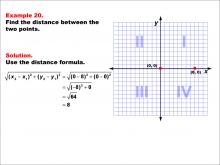
Math Example--Coordinate Geometry--Distance Formula: Example 20	Math Example--Coordinate Geometry--Distance Formula: Example 20 Topic Geometry Description This example illustrates the use of the distance formula to calculate the horizontal distance between two points on a coordinate plane. The points (0, 0) and (8, 0) are plotted on a graph, and the distance between them is determined using the formula: √((0 - 8)2 + (0 - 0)2) = √64 = 8.	The Distance Formula
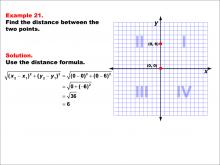
Math Example--Coordinate Geometry--Distance Formula: Example 21	Math Example--Coordinate Geometry--Distance Formula: Example 21 Topic Geometry Description This example demonstrates the application of the distance formula to find the vertical distance between two points on a coordinate plane. The points (0, 0) and (0, 6) are plotted on a graph, and the distance between them is calculated using the formula: √((0 - 0)2 + (0 - 6)2) = √(0 + (-6)2) = 6.	The Distance Formula
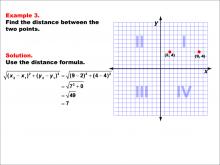
Math Example--Coordinate Geometry--Distance Formula: Example 3	Math Example--Coordinate Geometry--Distance Formula: Example 3 Topic Geometry Description This example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (2, 4) and (9, 4) are plotted on a graph, and the distance between them is calculated using the formula: √((9 - 2)2 + (4 - 4)2) = 7.	The Distance Formula
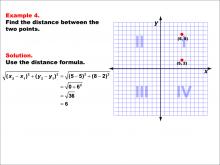
Math Example--Coordinate Geometry--Distance Formula: Example 4	Math Example--Coordinate Geometry--Distance Formula: Example 4 Topic Geometry Description This example illustrates the use of the distance formula to calculate the vertical distance between two points on a coordinate plane. The points (5, 8) and (5, 2) are plotted on a graph, and the distance between them is determined using the formula: √((5 - 5)2 + (8 - 2)2) = 6.	The Distance Formula
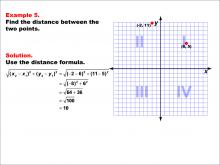
Math Example--Coordinate Geometry--Distance Formula: Example 5	Math Example--Coordinate Geometry--Distance Formula: Example 5 Topic Geometry Description This example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-2, 11) and (6, 5) are plotted on a graph, and the distance between them is calculated using the formula: √((-2 - 6)2 + (11 - 5)2) = 10.	The Distance Formula
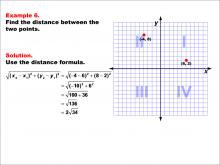
Math Example--Coordinate Geometry--Distance Formula: Example 6	Math Example--Coordinate Geometry--Distance Formula: Example 6 Topic Geometry Description This example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-4, 8) and (6, 2) are plotted on a graph, and the distance between them is determined using the formula: √((-4 - 6)2 + (8 - 2)2) = 2 √(34).	The Distance Formula
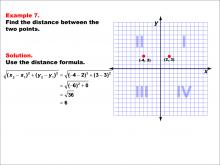
Math Example--Coordinate Geometry--Distance Formula: Example 7	Math Example--Coordinate Geometry--Distance Formula: Example 7 Topic Geometry Description This example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (-4, 3) and (2, 3) are plotted on a graph, and the distance between them is calculated using the formula: √((-4 - 2)2 + (3 - 3)2) = 6.	The Distance Formula
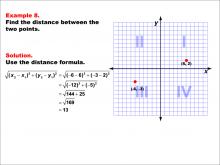
Math Example--Coordinate Geometry--Distance Formula: Example 8	Math Example--Coordinate Geometry--Distance Formula: Example 8 Topic Geometry Description This example illustrates the use of the distance formula to calculate the distance between two points on a coordinate plane. The points (-6, -3) and (6, 2) are plotted on a graph, and the distance between them is determined using the formula: √((-6 - 6)2 + (-3 - 2)2) = 13.	The Distance Formula
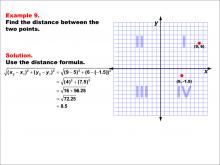
Math Example--Coordinate Geometry--Distance Formula: Example 9	Math Example--Coordinate Geometry--Distance Formula: Example 9 Topic Geometry Description This example demonstrates the application of the distance formula to find the distance between two points on a coordinate plane. The points (9, 6) and (5, -1.5) are plotted on a graph, and the distance between them is calculated using the formula: √((9 - 5)2 + (6 - (-1.5))2) = √(4^2 + 7.5^2) = √72.25 = 8.5.	The Distance Formula
Math Example--Quadratics--Calculating the Discriminant: Example 1	Calculating the Discriminant: Example 1 Topic Quadratics	Quadratic Formula
Math Example--Quadratics--Calculating the Discriminant: Example 10	Calculating the Discriminant: Example 10 Topic Quadratics Description This example illustrates a quadratic with two real roots. The discriminant being positive indicates that there are two real solutions to the equation. This scenario helps students recognize the significance of repeated roots and their graphical representation. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Formula
Math Example--Quadratics--Calculating the Discriminant: Example 2	Calculating the Discriminant: Example 2 Topic Quadratics	Quadratic Formula
Math Example--Quadratics--Calculating the Discriminant: Example 3	Calculating the Discriminant: Example 3 Topic Quadratics Description This example demonstrates a quadratic equation with one distinct real root, highlighting the relationship between the coefficients and the resulting discriminant. By calculating the discriminant, students can identify the nature of the roots, which is crucial for solving quadratics effectively. Skills involved include algebraic manipulation and understanding the graphical implications of roots. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Formula
Math Example--Quadratics--Calculating the Discriminant: Example 4	Calculating the Discriminant: Example 4 Topic Quadratics Description This example illustrates a quadratic with two real roots. The discriminant being positive indicates that there are two real roots. This scenario helps students recognize the significance of repeated roots and their graphical representation. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Formula
Math Example--Quadratics--Calculating the Discriminant: Example 5	Calculating the Discriminant: Example 5 Topic Quadratics Description This example demonstrates a quadratic equation with no distinct real roots, highlighting the relationship between the coefficients and the resulting discriminant. By calculating the discriminant, students can identify the nature of the roots, which is crucial for solving quadratics effectively. Skills involved include algebraic manipulation and understanding the graphical implications of roots. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Formula
Math Example--Quadratics--Calculating the Discriminant: Example 6	Calculating the Discriminant: Example 6 Topic Quadratics Description This example illustrates a quadratic with a double real root. The discriminant being zero indicates that there is exactly one real solution to the equation. This scenario helps students recognize the significance of repeated roots and their graphical representation. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Formula
Math Example--Quadratics--Calculating the Discriminant: Example 7	Calculating the Discriminant: Example 7 Topic Quadratics Description In this example, the quadratic equation results in two roots, demonstrating the cases where the discriminant is positive. This provides insights into scenarios where quadratic equations intersect the x-axis twice. Skills in algebra are focused on interpreting complex solutions and their geometric implications. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Formula
Math Example--Quadratics--Calculating the Discriminant: Example 8	Calculating the Discriminant: Example 8 Topic Quadratics Description This example illustrates a quadratic with two real roots. The discriminant being positive indicates that there are two real solutions to the equation. This scenario helps students recognize the significance of two roots and their graphical representation. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Formula
Math Example--Quadratics--Calculating the Discriminant: Example 9	Calculating the Discriminant: Example 9 Topic Quadratics Description This example demonstrates a quadratic equation with two distinct real roots, highlighting the relationship between the coefficients and the resulting discriminant. By calculating the discriminant, students can identify the nature of the roots, which is crucial for solving quadratics effectively. Skills involved include algebraic manipulation and understanding the graphical implications of roots. For a complete collection of math examples related to Quadratics click on this link: Math Examples: Quadratics Collection.	Quadratic Formula
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 1	Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 1 This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.	Rational Expressions
Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 10	Math Example--Rational Concepts--Rational Approximations of Irrational Numbers--Example 10 This is part of a collection of math examples that focus on rational number concepts. This includes rational numbers, expressions, and functions.	Rational Expressions