
Illustrative Math Alignment: Grade 8 Unit 6
Associations in Data
Lesson 8: Analyzing Bivariate Data
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Math Tutorials Collection: Applications of Linear Functions |
OverviewThis collection aggregates a set of tutorials on Applications of Linear Functions. There are a total of 10 tutorials. |
Applications of Linear Functions and Proportions |

|
Quadratics Collection: Texas Instruments Graphing Calculator Resources |
A set of resources for the TI-Nspire, TI-Nspire CX, and the Nspire App.
|
Applications of Quadratic Functions, Graphs of Quadratic Functions, Quadratic Formula, Data Analysis, Quadratic Equations and Functions, Inequalities and Composite Functions |

|
Math in the News Collection: Business Math |
OverviewThis is a collection of issues of Math in the News that deal with business applications.
|
Applications of Exponential and Logarithmic Functions, Data Analysis and Volume |

|
Math in the News Collection: Applications of Data Analysis |
OverviewThis is a collection of Math in the News stories that focus on the topic of Data Analysis.
|
Data Analysis, Data Gathering, Probability, Percents and Ratios and Rates |

|
Math Examples Collection: Charts, Graphs, and Plots |
OverviewThis collection aggregates all the math examples around the topic of Charts, Graphs, and Plots. There are a total of 38 Math Examples. This collection of resources is made up of downloadable PNG images that you can easily incorporate into your lesson plans.To learn more about Media4Math's Math Examples, click on this video link.
|
Slope-Intercept Form, Data Analysis, Point-Slope Form and Subtraction Facts to 100 |
|
Math Definitions Collection: Linear Functions | OverviewThe collection of definitions on the topic of Linear Functions from Media4Math is an invaluable resource for students and educators alike. This comprehensive set includes essential terms such as slope, y-intercept, linear function, and rate of change. Understanding these terms is crucial for mastering the concept of linear functions, which are foundational in algebra and essential for advanced mathematical studies. |
Slope-Intercept Form, Applications of Linear Functions, Graphs of Linear Functions, Standard Form, Point-Slope Form and Slope |

|
Math Video Collection: Texas Instruments Tutorial Videos |
OverviewThis collection aggregates all the math videos and resources in this series: Texas Instruments Tutorial Videos. There are a total of 266 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.
|
Rational Expressions, Sequences, Series, Polynomial Functions and Equations, Graphs of Quadratic Functions, Quadratic Equations and Functions, Solving Systems of Equations, Trig Expressions and Identities, Probability, Geometric Constructions with Triangles, Composite Functions, Geometric Constructions with Angles and Planes, Distance Formula, Data Analysis, Slope, Special Functions, Trigonometric Functions, Graphs of Exponential and Logarithmic Functions, Radical Functions and Equations, Rational Functions and Equations, Slope-Intercept Form, Coordinate Systems, Graphs of Linear Functions, Inequalities, Matrix Operations and Midpoint Formula |

|
Math Video Collection: Algebra Applications Video Series: Data Analysis |
OverviewThis collection aggregates all the math videos and resources in this series: Algebra Applications Video Series: Data Analysis. There are a total of 26 resources. This collection of resources is made up of downloadable MP4, transcripts, and other resources files that you can easily incorporate into a presentation.
|
Data Analysis and Data Gathering |
|
Math Examples Collection: Analyzing Scatterplots |
OverviewThis collection aggregates all the math examples around the topic of Analyzing Scatterplots. There are a total of 10 Math Examples. This collection of resources is made up of downloadable PNG images that you can easily incorporate into your lesson plans.
|
Data Analysis |

|
Linear Functions and Equations Collection: Applications of Linear Functions | Here are a number of PowerPoint presentations that focus on different applications of linear functions. |
Applications of Linear Functions, Proportions and Definition of a Polygon |

|
Linear Functions and Equations Collection: Basic Terms | This collection includes key term, definitions, and formulas. | Slope-Intercept Form, Applications of Linear Functions and Slope |

|
VIDEO: Algebra Applications: Data Analysis | VIDEO: Algebra Applications: Data Analysis
TopicData Analysis |
Data Analysis and Data Gathering |

|
VIDEO: Algebra Nspirations: Data Analysis and Probability | VIDEO: Algebra Nspirations: Data Analysis and Probability
TopicData Analysis |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Multiseries Scatterplot | Closed Captioned Video: Multiseries Scatterplot
In this TI Nspire tutorial, Spreadsheet and Graph windows are used to graph a multiseries scatterplot. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. This is part of a collection of closed captioned videos on various math topics. To see the complete collection of the videos, click on this link. Note: The download is Media4Math's guide to closed captioned videos.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Video TranscriptsThis video has a transcript available. To see the complete collection of video transcripts, click on this link. |
Data Analysis |

|
Closed Captioned Video: Scatterplot 1 | Closed Captioned Video: Scatterplot 1
In this TI Nspire tutorial, Spreadsheet and Graph windows are used to graph a scatterplot. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. This is part of a collection of closed captioned videos on various math topics. To see the complete collection of the videos, click on this link. Note: The download is Media4Math's guide to closed captioned videos.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Video TranscriptsThis video has a transcript available. To see the complete collection of video transcripts, click on this link. |
Data Analysis |

|
Closed Captioned Video: Scatterplot 2 | Closed Captioned Video: Scatterplot 2
In this TI Nspire tutorial, Spreadsheet and Statistics windows are used to graph a scatterplot. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. This is part of a collection of closed captioned videos on various math topics. To see the complete collection of the videos, click on this link. Note: The download is Media4Math's guide to closed captioned videos.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Video TranscriptsThis video has a transcript available. To see the complete collection of video transcripts, click on this link. |
Data Analysis |

|
Closed Captioned Video: A Probability Simulation 2 | Closed Captioned Video: A Probability Simulation 2
In this TI Nspire tutorial, the Spreadsheet and Statistics windows are used to create a probability simulation of a coin toss. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. . |
Probability |

|
Closed Captioned Video: A Probability Simulation 3 | Closed Captioned Video: A Probability Simulation 3
In this TI Nspire tutorial, the Spreadsheet and Statistics windows are used to create a probability simulation of tossing two coins. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. . |
Probability |

|
Closed Captioned Video: Algebra Applications: Data Analysis | Closed Captioned Video: Algebra Applications: Data AnalysisTopicData Analysis |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Algebra Applications: Data Analysis, 1 | Closed Captioned Video: Algebra Applications: Data Analysis, 1TopicData Analysis DescriptionThis segment introduces the 2008 mortgage crisis, explaining how mortgage defaults caused widespread economic repercussions, including a recession. It outlines basic mortgage concepts such as loan amount, interest rate, and repayment periods. Key terms include mortgage, interest rate, and amortization. The segment sets the stage for exploring how specific mortgage types, like subprime loans, led to financial instability. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Algebra Applications: Data Analysis, 2 | Closed Captioned Video: Algebra Applications: Data Analysis, 2TopicData Analysis DescriptionThe video defines a mortgage as a long-term loan used to purchase a home and explains its components: loan amount, interest rate, and payment periods. Through examples, it demonstrates how interest rates impact total loan costs. Key concepts include amortization, equity, and principal versus interest payments. Applications involve using financial calculators to analyze repayment schedules and equity growth, emphasizing the importance of interest rates. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Algebra Applications: Data Analysis, 3 | Closed Captioned Video: Algebra Applications: Data Analysis, 3TopicData Analysis DescriptionThis segment explains subprime mortgages, emphasizing how credit scores affect loan interest rates. It compares repayment scenarios for borrowers with different FICO scores, showing the financial challenges of subprime loans. Key terms include subprime mortgage, credit risk, and delinquency. The video uses simulations to illustrate the likelihood and impact of loan defaults, linking these trends to the mortgage crisis. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Algebra Applications: Data Analysis, 4 | Closed Captioned Video: Algebra Applications: Data Analysis, 4TopicData Analysis DescriptionAdjustable-rate mortgages (ARMs) are discussed, focusing on their role in the 2008 crisis. It demonstrates how variable rates increase long-term costs and create financial risks. Concepts include loan balance, refinancing, and amortization. The video uses spreadsheets to show payment changes over time and their economic effects. Applications highlight real-world implications of rising interest rates and decreasing home values. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Algebra Nspirations: Data Analysis and Probability | Closed Captioned Video: Algebra Nspirations: Data Analysis and Probability
What are the two meanings of statistics? What does it really mean that an event has a 50% probability of occurring? Why are data analysis and probability always taught together? Written and hosted by internationally acclaimed math educator Dr. Monica Neagoy, this video answers these questions and addresses fundamental concepts such as the law of large numbers and the notion of regression analysis. Both engaging investigations are based on true stories and real data, utilize different Nspire applications, and model the seamless connection among various problem representations. Concepts explored: statistics, data analysis, regression analysis. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Algebra Nspirations: Data Analysis and Probability, 1 | Closed Captioned Video: Algebra Nspirations: Data Analysis and Probability, Segment 1
In this Investigation we explore uncertainty and randomness. This video is Segment 1 of a 4 segment series related to Data Analysis and Probability. Segments 1 and 2 are grouped together. |
Data Analysis and Data Gathering |
|
Closed Captioned Video: Algebra Nspirations: Data Analysis and Probability, 3 | Closed Captioned Video: Algebra Nspirations: Data Analysis and Probability, Segment 3
In this Investigation we look at real-world data involving endangered wolf populations. This video is Segment 3 of a 4 segment series related to Data Analysis and Probability. Segments 3 and 4 are grouped together. |
Data Analysis and Data Gathering |

|
Closed Captioned Video: Probability Simulation 1 | Closed Captioned Video: Probability Simulation 1
In this TI Nspire tutorialthe Spreadsheet and Statistics windows are used to create a probability simulation of tossing two dice. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. . |
Probability |

|
Closed Captioned Video: Random Number Table | Closed Captioned Video: Random Number Table
In this TI Nspire tutorial, the Spreadsheet window is used to create a random number table. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. . This is part of a collection of closed captioned videos on various math topics. To see the complete collection of the videos, click on this link. Note: The download is Media4Math's guide to closed captioned videos.Related ResourcesTo see additional resources on this topic, click on the Related Resources tab.Video TranscriptsThis video has a transcript available. To see the complete collection of video transcripts, click on this link. |
Probability |

|
Collections in a Box: Slope Formula | This cheat sheet gathers together a number of resources on the topic of the slope formula. See the descriptions and links below. Each link takes you to a collection of resources around that topic. The middle column indicates the number of resources available and the third column takes you to page on Media4Math where those resources can be found. Subscribers can download the PDF version of this cheat sheet. Click Preview to see the HTML version. |
Point-Slope Form, Slope and Slope-Intercept Form |
|
Definition--Linear Function Concepts--Constant Function | Constant Function
TopicLinear Functions DefinitionA constant function is a linear function of the form f(x) = b, where b is a constant. The graph of a constant function is a horizontal line. DescriptionConstant functions are a fundamental concept in linear functions. They represent scenarios where the output value remains unchanged, regardless of the input value. This is depicted graphically as a horizontal line, indicating that the function's rate of change is zero. In real-world applications, constant functions can model situations where a quantity remains steady over time. For example, a flat fee service charge that does not vary with usage can be represented as a constant function. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Converting from Standard Form to Slope-Intercept Form | Converting from Standard Form to Slope-Intercept Form
TopicLinear Functions DefinitionConverting from standard form to slope-intercept form involves rewriting a linear equation from the form Ax + By = C to the form y = mx + b, where m is the slope and b is the y-intercept. DescriptionConverting linear equations from standard form to slope-intercept form is a key skill in algebra. This conversion allows for easier graphing and interpretation of the equation's slope and y-intercept. |
Slope-Intercept Form |
|
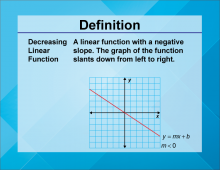
Definition--Linear Function Concepts--Decreasing Linear Function | Decreasing Linear Function
TopicLinear Functions DefinitionA decreasing linear function is a linear function where the slope is negative, indicating that as the input value increases, the output value decreases. DescriptionDecreasing linear functions are important in understanding how variables inversely relate to each other. The negative slope signifies a reduction in the dependent variable as the independent variable increases. Real-world examples include depreciation of assets over time or the decrease in temperature as altitude increases. These functions help model scenarios where an increase in one quantity results in a decrease in another. |
Slope-Intercept Form |
|
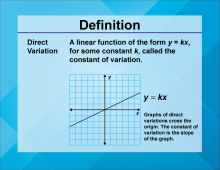
Definition--Linear Function Concepts--Direct Variation | Direct Variation
TopicLinear Functions DefinitionDirect variation describes a linear relationship between two variables where one variable is a constant multiple of the other, expressed as y = kx, where k is the constant of variation. DescriptionDirect variation is a fundamental concept in linear functions, illustrating how one variable changes proportionally with another. The constant of variation, k, represents the rate of change. In real-world scenarios, direct variation can model relationships such as speed and distance, where distance traveled varies directly with time at a constant speed. Understanding this concept is crucial in fields like physics and engineering. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Equations of Parallel Lines | Equations of Parallel Lines
TopicLinear Functions DefinitionEquations of parallel lines are linear equations that have the same slope but different y-intercepts, indicating that the lines never intersect. DescriptionUnderstanding equations of parallel lines is crucial in geometry and algebra. Parallel lines have identical slopes, which means they run in the same direction and never meet. In real-world applications, parallel lines can model scenarios such as railway tracks or lanes on a highway, where maintaining a consistent distance is essential. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Equations of Perpendicular Lines | Equations of Perpendicular Lines
TopicLinear Functions DefinitionEquations of perpendicular lines are linear equations where the slopes are negative reciprocals of each other, indicating that the lines intersect at a right angle. DescriptionEquations of perpendicular lines are significant in both geometry and algebra. The negative reciprocal relationship between their slopes ensures that the lines intersect at a 90-degree angle. In real-world applications, perpendicular lines are found in various structures, such as the intersection of streets or the corners of a building, where right angles are essential. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--Identity Function | Identity Function
TopicLinear Functions DefinitionAn identity function is a linear function of the form f(x) = x, where the output is equal to the input for all values of x. DescriptionThe identity function is a basic yet crucial concept in linear functions. It represents a scenario where the input value is always equal to the output value, graphically depicted as a 45-degree line passing through the origin. In real-world applications, the identity function can model situations where input and output are directly proportional and identical, such as converting units of the same measure. This also introduces the concept of identity, which is fundamental to mathematics. |
Slope-Intercept Form |
|
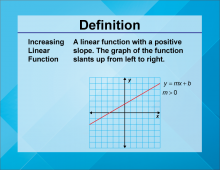
Definition--Linear Function Concepts--Increasing Linear Function | Increasing Linear Function
TopicLinear Functions DefinitionAn increasing linear function is a linear function where the slope is positive, indicating that as the input value increases, the output value also increases. DescriptionIncreasing linear functions are essential in understanding how variables positively relate to each other. The positive slope signifies an increase in the dependent variable as the independent variable increases. Real-world examples include income increasing with hours worked or the rise in temperature with the increase in daylight hours. These functions help model scenarios where an increase in one quantity results in an increase in another. |
Slope-Intercept Form |
|
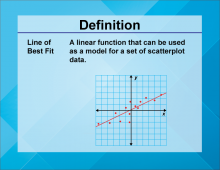
Definition--Linear Function Concepts--Line of Best Fit | Line of Best Fit
TopicLinear Functions DefinitionA line of best fit is a straight line that best represents the data on a scatter plot, showing the trend of the data points. DescriptionThe line of best fit is a crucial concept in statistics and data analysis. It helps in identifying the trend and making predictions based on the data. In real-world applications, the line of best fit is used in various fields such as economics, biology, and engineering to analyze trends and make forecasts. For example, it can be used to predict future sales based on past data. |
Graphs of Linear Functions |

|
Definition--Linear Function Concepts--Linear Equations in Standard Form | Linear Equations in Standard Form
TopicLinear Functions DefinitionLinear equations in standard form are written as Ax + By = C, where A, B, and C are constants, and A and B are not both zero. DescriptionLinear equations in standard form are a fundamental representation of linear functions. They provide a way to express linear relationships in a general form. |
Standard Form |
|
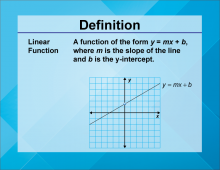
Definition--Linear Function Concepts--Linear Function | Linear Function
TopicLinear Functions DefinitionA linear function is a function that can be graphed as a straight line, typically written in the form y = mx + b, where m is the slope and b is the y-intercept. DescriptionLinear functions are one of the most fundamental concepts in mathematics. They describe relationships where the rate of change between variables is constant, represented graphically as a straight line. This simplicity makes them a central topic in algebra and calculus. |
Slope-Intercept Form |
|
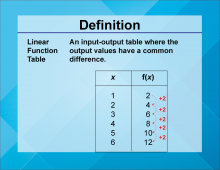
Definition--Linear Function Concepts--Linear Function Tables | Linear Function Tables
TopicLinear Functions DefinitionLinear function tables display the input-output pairs of a linear function, showing how the dependent variable changes with the independent variable. DescriptionLinear function tables are useful tools for understanding and analyzing linear relationships. They provide a clear way to see how changes in the input (independent variable) affect the output (dependent variable). |
Applications of Linear Functions and Graphs of Linear Functions |
|
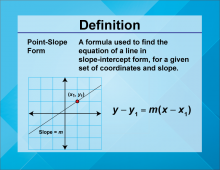
Definition--Linear Function Concepts--Point-Slope Form | Point-Slope Form
TopicLinear Functions DefinitionPoint-slope form of a linear equation is written as y − y1 = m(x−x1 ), where m is the slope and (x1 ,y1) is a point on the line. DescriptionThe point-slope form is a versatile way to express linear equations, especially useful when you know a point on the line and the slope. It allows for quick construction of the equation of a line. |
Point-Slope Form |
|
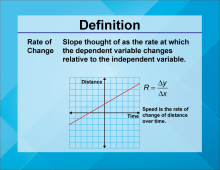
Definition--Linear Function Concepts--Rate of Change | Rate of Change
TopicLinear Functions DefinitionRate of change in a linear function is the ratio of the change in the dependent variable to the change in the independent variable, often represented as the slope m in the equation y = mx + b. DescriptionRate of change is a fundamental concept in understanding linear functions. It describes how one variable changes in relation to another, and is graphically represented by the slope of a line. |
Slope |

|
Definition--Linear Function Concepts--Slope-Intercept Form | Slope-Intercept Form
TopicLinear Functions DefinitionSlope-intercept form of a linear equation is written as y = mx + b, where m is the slope and b is the y-intercept. DescriptionSlope-intercept form is one of the most commonly used forms of linear equations. It provides a clear way to understand the slope and y-intercept of a line, making it easier to graph and interpret. In real-world applications, slope-intercept form is used in various fields such as economics, physics, and engineering to model linear relationships. For example, it can represent the relationship between cost and production levels in business. |
Slope-Intercept Form |

|
Definition--Linear Function Concepts--The Equation of a Line From Two Coordinates | The Equation of a Line From Two Coordinates
TopicLinear Functions DefinitionThe equation of a line from two coordinates can be determined by finding the slope between the two points and using it in the point-slope form of a linear equation. DescriptionFinding the equation of a line from two coordinates is a fundamental skill in algebra. It involves calculating the slope between the two points and then using one of the points to form the equation in point-slope or slope-intercept form. |
Point-Slope Form |
|
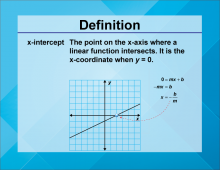
Definition--Linear Function Concepts--x-Intercept | x-Intercept
TopicLinear Functions DefinitionThe x-intercept is the point where a graph crosses the x-axis, indicating the value of x when 𝑦 y is zero. DescriptionThe x-intercept is a key concept in understanding the behavior of linear functions. It represents the point where the function's output is zero, providing insight into the function's roots and behavior. In real-world applications, the x-intercept can be used to determine break-even points in business, where revenue equals costs, or to find the time at which a process starts or stops. |
Slope-Intercept Form |
|
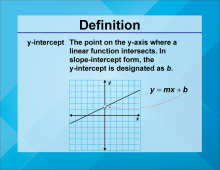
Definition--Linear Function Concepts--y-Intercept | y-Intercept
TopicLinear Functions DefinitionThe y-intercept is the point where a graph crosses the y-axis, indicating the value of y when x is zero. DescriptionThe y-intercept is a fundamental concept in understanding the behavior of linear functions. It represents the initial value of the function when the input is zero, providing insight into the function's starting point. In real-world applications, the y-intercept can be used to determine initial conditions in various scenarios, such as the starting balance in a bank account or the initial position of an object in motion. |
Slope-Intercept Form |

|
INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop | INSTRUCTIONAL RESOURCE: Algebra Application: The Rise of K-Pop
In this Algebra Application, students examine the music industry, specifically the rise of Korean pop music, or K-Pop. Using industry data students examine tables and graphs of categorical data before identifying possible functional relationships. A mathematical model is developed to explore the relationship between viral videos and sales. Topics covered: Mathematical modeling, Linear regression, Categorical data, Functions. |
Applications of Linear Functions and Data Analysis |

|
INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable? | INSTRUCTIONAL RESOURCE: Algebra Application: When Will Space Travel Be Affordable?
In this Algebra Application, students examine the budding industry of commercial space travel. Using data from the Bureau of Transportation Statistics, students build a mathematical model from historical airfare data. This model is used to predict when commercial space travel will become affordable. This also includes a discussion of inflation-adjusted costs and the future value of money. Topics covered: Mathematical modeling, Linear regression, Exponential functions, The time value of money. |
Applications of Exponential and Logarithmic Functions, Applications of Linear Functions and Data Analysis |

|
Instructional Resource: Applications of Linear Functions: Circumference vs. Diameter | In this Slide Show, apply concepts of linear functions to the context of circumference vs. diameter. Note: The download is a PPT file. Related ResourcesTo see the complete collection of Tutorials on this topic, click on this link: https://bit.ly/3g0P3cN |
Applications of Linear Functions |