
Illustrative Math Alignment: Grade 6 Unit 1
Reasoning to Find Area
Lesson 13: Polyhedra
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Animated Math Clip Art--3D Geometry--Surface Area |
Surface AreaTopic3D Geometry DescriptionThis animation illustrates the concept of surface area for a 3D shape. It shows how the surface of a three-dimensional object can be "unfolded" or "unwrapped" to reveal all its faces or surfaces, which can then be measured to calculate the total surface area. Using animated math clip art like this helps students visualize the abstract concept of surface area. Teachers can use this to explain how to calculate surface area for various 3D shapes and discuss real-world applications of this concept. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Tetrahedron |
TetrahedronTopic3D Geometry DescriptionThis animation shows a tetrahedron, a three-dimensional shape with four triangular faces. It's the simplest of all the Platonic solids and has applications in both mathematics and chemistry. Animated math clip art like this is crucial for teaching as it allows students to visualize complex 3D shapes from different angles. Teachers can use this to discuss properties of polyhedra, symmetry, and geometric relationships. Here's a potential script for teachers: "Examine this tetrahedron. Count its faces, edges, and vertices. How does it compare to other 3D shapes we've studied? Can you think of any real-world objects that resemble a tetrahedron?" |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Tetrahedron with Horizontal Cross-Section |
Tetrahedron with Horizontal Cross-SectionTopic3D Geometry DescriptionThis animation depicts a tetrahedron with a horizontal cross-section. It shows how slicing the tetrahedron parallel to its base results in a triangular cross-section that decreases in size as it moves towards the apex. Using animated math clip art like this helps students understand the internal structure of complex 3D shapes. Teachers can use this to discuss concepts such as similarity, proportions, and how cross-sections relate to the volume of a tetrahedron. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Tetrahedron with Vertical Cross-Section |
Tetrahedron with Vertical Cross-SectionTopic3D Geometry DescriptionThis animation shows a tetrahedron with a vertical cross-section. It illustrates how slicing the tetrahedron vertically through its apex results in a triangular cross-section, revealing the internal structure and symmetry of the shape. Animated math clip art like this is valuable for teaching as it provides a different perspective on the internal geometry of complex 3D shapes. Teachers can use this to discuss concepts such as symmetry, slant height, and how vertical cross-sections relate to the surface area of a tetrahedron. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Triangular Prism |
Triangular PrismTopic3D Geometry DescriptionThis animation depicts a triangular prism, a three-dimensional shape with two triangular bases and three rectangular faces. It's an important shape in geometry with various real-world applications. Using animated math clip art like this helps students visualize 3D shapes from different angles. Teachers can use this to explain concepts of volume, surface area, and properties of prisms. Here's a potential script for teachers: "Observe this triangular prism. Can you identify its bases and lateral faces? How would you calculate its volume and surface area? Can you think of any objects in real life that have this shape?" |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Triangular Prism with Horizontal Cross-Section |
Triangular Prism with Horizontal Cross-SectionTopic3D Geometry DescriptionThis animation shows a triangular prism with a horizontal cross-section. It illustrates that slicing the prism parallel to its base results in a rectangular cross-section that varies in size depending on the location of the slice. Animated math clip art like this helps students understand the internal structure of prisms. Teachers can use this to discuss concepts such as congruence, cross-sectional area, and how this relates to the volume of a prism. |
3-Dimensional Figures |

|
Animated Math Clip Art--3D Geometry--Triangular Prism with Vertical Cross-Section |
Triangular Prism with Vertical Cross-SectionTopic3D Geometry DescriptionThis animation depicts a triangular prism with a vertical cross-section. It shows how slicing the prism vertically results in a triangular cross-section, and all such triangles are congruent along the length of the prism. Using animated math clip art like this provides students with a different perspective on the internal geometry of prisms. Teachers can use this to discuss concepts such as height, lateral area, and how vertical cross-sections relate to the surface area of a prism. |
3-Dimensional Figures |

|
Closed Captioned Video: Geometry Applications: 3D Geometry |
Closed Captioned Video: Geometry Applications: 3D GeometryTopic3D Geometry |
3-Dimensional Figures and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 1 |
Closed Captioned Video: Geometry Applications: 3D Geometry, 1Topic3D Geometry DescriptionDescription: This segment introduces Platonic solids, including tetrahedron, cube, and dodecahedron, emphasizing their congruent edges, vertices, and angles. It connects these geometric figures to both natural and man-made structures, setting the stage for exploring 3D geometry applications. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 2 |
Closed Captioned Video: Geometry Applications: 3D Geometry, 2Topic3D Geometry DescriptionDescription: This segment explores pyramids, particularly Mayan and Egyptian structures, to distinguish rectangular and square bases. It discusses the volume of truncated pyramids using proportional relationships and introduces the concept of tiered volume reduction through geometric sequences. |
3-Dimensional Figures, Pyramids and Applications of 3D Geometry |

|
Closed Captioned Video: Geometry Applications: 3D Geometry, 3 |
Closed Captioned Video: Geometry Applications: 3D Geometry, 3Topic3D Geometry DescriptionDescription: This segment examines cylinders, using the Shanghai Tower as a case study. It highlights how adjustments to height and radius affect volume and surface area, demonstrating these principles with geometric calculations and their architectural applications in energy efficiency. |
3-Dimensional Figures, Cylinders and Applications of 3D Geometry |

|
Definition--3D Geometry Concepts--Antiprism |
AntiprismTopic3D Geometry DefinitionAn antiprism is a polyhedron composed of two parallel copies of an n-sided polygon, connected by an alternating band of triangles. DescriptionAntiprisms are fascinating three-dimensional geometric figures that play a significant role in the study of polyhedra and spatial geometry. Unlike prisms, which have rectangular lateral faces, antiprisms feature triangular faces connecting their two parallel polygonal bases. This unique structure gives antiprisms distinct properties and applications in various fields of mathematics and engineering. |
3-Dimensional Figures |
|
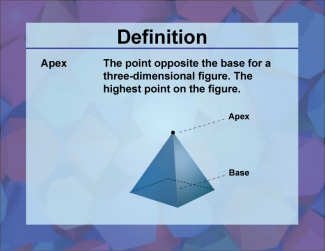
Definition--3D Geometry Concepts--Apex |
ApexTopic3D Geometry DefinitionThe apex is the highest point or vertex of a three-dimensional figure, typically opposite to and furthest from its base. DescriptionIn the realm of three-dimensional geometry, the concept of an apex plays a crucial role in defining and understanding various geometric solids. The apex is particularly significant in figures such as cones and pyramids, where it represents the culminating point of the structure. For a cone, the apex is the single point at the top where all the lateral lines or edges converge. In a pyramid, it's the vertex where all the triangular faces meet, forming the pinnacle of the shape. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Base (Geometry) |
Geometric Base in 3D GeometryTopic3D Geometry DefinitionA geometric base is the face of a three-dimensional figure from which the height is measured. DescriptionIn the context of three-dimensional geometry, the term "geometric base" is crucial for understanding the structure and properties of various 3D shapes. The base of a 3D figure is typically a flat surface, often a polygon, from which the height of the figure is perpendicular. This concept is fundamental when calculating the volume and surface area of three-dimensional shapes such as prisms, cylinders, pyramids, and cones. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Edge |
EdgeTopic3D Geometry DefinitionAn edge in three-dimensional geometry is the line segment where two faces of a 3D shape meet. DescriptionIn the study of three-dimensional geometry, an edge is a fundamental concept that helps define the structure and properties of 3D shapes. Each edge is formed by the intersection of two faces, and it is a critical component in determining the overall shape and form of a 3D object. For instance, a cube has 12 edges, each formed by the meeting of two square faces. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Face |
Face of a 3D FigureTopic3D Geometry DefinitionA face is a flat surface that forms part of the boundary of a three-dimensional figure. DescriptionIn the realm of three-dimensional geometry, the concept of a face is fundamental to understanding the structure and properties of 3D figures. A face represents one of the flat, two-dimensional surfaces that enclose a three-dimensional object. These surfaces play a crucial role in defining the shape, volume, and surface area of 3D figures. |
3-Dimensional Figures |
|
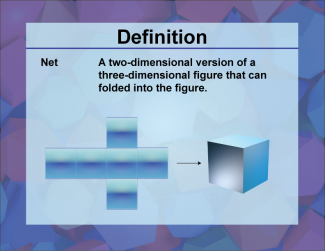
Definition--3D Geometry Concepts--Net |
Net of a 3D FigureTopic3D Geometry DefinitionA net is a two-dimensional shape that can be folded to form a three-dimensional figure. DescriptionIn the realm of three-dimensional geometry, a net is an essential concept that helps in visualizing and constructing 3D shapes. A net is essentially a two-dimensional pattern that, when folded along specific lines, forms a three-dimensional object. This concept is particularly useful in understanding the properties and structures of 3D figures such as cubes, pyramids, and prisms. |
3-Dimensional Figures |
|
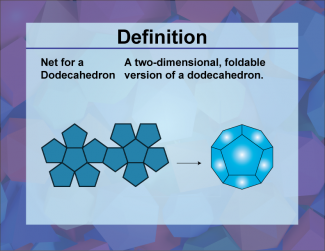
Definition--3D Geometry Concepts--Net for a Dodecahedron |
Net for a DodecahedronTopic3D Geometry. DefinitionA net for a dodecahedron is a two-dimensional figure that can be folded to form a three-dimensional dodecahedron. DescriptionThe dodecahedron is one of the five Platonic solids, characterized by its twelve regular pentagonal faces, thirty edges, and twenty vertices. Understanding the net of a dodecahedron helps in visualizing and constructing this complex polyhedron from a flat sheet. |
3-Dimensional Figures |
|
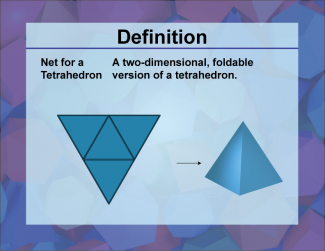
Definition--3D Geometry Concepts--Net for a Tetrahedron |
Net for a TetrahedronTopic3D Geometry DefinitionA net for a tetrahedron is a two-dimensional pattern that can be folded to form a three-dimensional tetrahedron, which is a polyhedron with four triangular faces. DescriptionIn the realm of three-dimensional geometry, the concept of a net is crucial for understanding the structure and properties of polyhedra. A tetrahedron, one of the simplest forms of polyhedra, consists of four triangular faces, six edges, and four vertices. The net of a tetrahedron is a flat, two-dimensional figure that, when folded along its edges, forms the three-dimensional shape of the tetrahedron. |
3-Dimensional Figures |
|
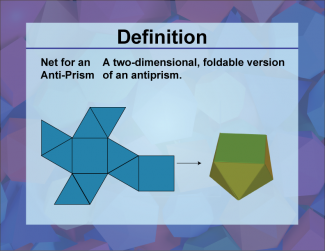
Definition--3D Geometry Concepts--Net for an Antiprism |
Net for an AntiprismTopic3D Geometry. DefinitionA net for an antiprism is a two-dimensional shape that can be folded to form a three-dimensional antiprism, which is a type of polyhedron with two parallel polygonal bases connected by an alternating band of triangles. DescriptionIn the realm of three-dimensional geometry, an antiprism is a fascinating polyhedron that extends the concept of prisms. Unlike regular prisms, which have two parallel bases connected by rectangular faces, antiprisms have two parallel bases connected by an alternating band of triangles. This unique structure results in a more complex and often more visually interesting shape. |
3-Dimensional Figures |
|
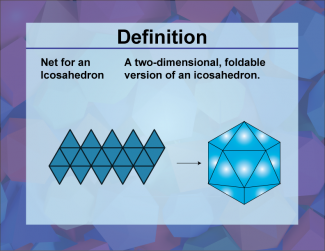
Definition--3D Geometry Concepts--Net for an Icosahedron |
Net for an IcosahedronTopic3D Geometry DefinitionA net for an icosahedron is a two-dimensional flat pattern that, when folded along its edges, forms the surface of a three-dimensional icosahedron. DescriptionThe net for an icosahedron is a crucial concept in three-dimensional geometry, particularly in the study of polyhedra. An icosahedron is a regular polyhedron with 20 faces, each of which is an equilateral triangle. The net provides a visual representation of how these 20 triangular faces are connected and arranged in a flat pattern that can be folded to create the three-dimensional shape. |
3-Dimensional Figures |
|
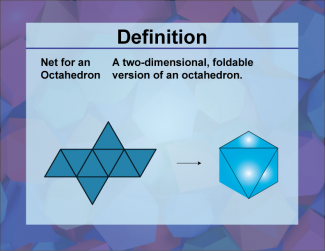
Definition--3D Geometry Concepts--Net for an Octahedron |
Net for an OctahedronTopic3D Geometry DefinitionA net for an octahedron is a two-dimensional figure that can be folded to form a three-dimensional octahedron. DescriptionIn the realm of three-dimensional geometry, a net is a crucial concept that helps in visualizing and constructing 3D shapes from 2D representations. Specifically, a net for an octahedron consists of eight equilateral triangles arranged in a specific pattern. When these triangles are folded along the edges, they form an octahedron, which is a polyhedron with eight faces, twelve edges, and six vertices. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Platonic Solids |
Platonic SolidsTopic3D Geometry DefinitionA Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space, where each face is a congruent regular polygon, and the same number of faces meet at each vertex. DescriptionPlatonic solids are fundamental constructs in the study of three-dimensional geometry. These solids are unique because they are the only five regular polyhedra that exist. Each Platonic solid has faces that are congruent regular polygons, and the same number of faces meet at each vertex, making them highly symmetrical and aesthetically pleasing. The five Platonic solids are the tetrahedron, cube, octahedron, dodecahedron, and icosahedron, each named for its number of faces. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Prism |
PrismTopic3D Geometry DefinitionA prism is a three-dimensional solid object with two identical polygonal bases connected by parallelogram faces. DescriptionIn the realm of three-dimensional geometry, a prism is a polyhedron with two parallel, congruent bases connected by rectangular or parallelogram faces. The defining characteristic of a prism is that its cross-sections parallel to the bases are identical to the bases themselves. This property makes prisms a significant topic of study in geometry. |
3-Dimensional Figures |

|
Definition--3D Geometry Concepts--Slant Height |
Slant HeightTopic3D Geometry DefinitionSlant height is the distance measured along a lateral face from the base to the apex of a three-dimensional figure, such as a pyramid or a cone. DescriptionIn the context of three-dimensional geometry, the slant height is a crucial measurement for various solid figures, particularly right pyramids and right circular cones. It represents the shortest path along the surface of the figure from the apex (top point) to the base, distinguishing it from the vertical height which measures the perpendicular distance from the apex to the center of the base. |
3-Dimensional Figures |
|
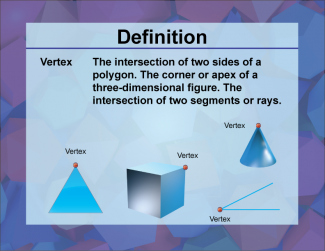
Definition--3D Geometry Concepts--Vertex |
Vertex in 3D GeometryTopic3D Geometry DefinitionA vertex is a point where three or more edges meet in a three-dimensional figure. DescriptionIn the study of three-dimensional geometry, the term vertex is fundamental. A vertex is a critical point in any 3D geometric shape, marking the intersection of edges. For example, in a cube, each corner where the edges converge is a vertex. Vertices are essential in defining the shape and structure of 3D figures, as they help in understanding the spatial relationships between different parts of the figure. |
3-Dimensional Figures |
|
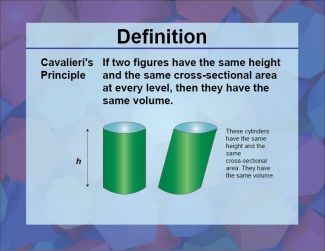
Definition--3D Geometry Concepts--Cavalieri's Principle |
Cavalieri's PrincipleTopic3D Geometry DefinitionCavalieri's Principle states that if two solids are contained between two parallel planes, and every plane parallel to these planes intersects both solids in cross-sections of equal area, then the two solids have equal volumes. DescriptionCavalieri's Principle is a fundamental concept in three-dimensional geometry that provides a method for determining the volume of solids. Named after the Italian mathematician Bonaventura Cavalieri, this principle is particularly useful for comparing the volumes of solids that might not have straightforward geometric shapes. |
3-Dimensional Figures |

|
Definition--Geometry Basics--Antiprism |
AntiprismTopicGeometry Basics DefinitionA polyhedron with two parallel faces and other faces that are triangular. DescriptionAn antiprism is a type of polyhedron that has two parallel faces connected by an alternating band of triangles. This geometric shape is significant in advanced geometry and has applications in fields such as crystallography and molecular chemistry. Understanding antiprisms helps in comprehending the properties of polyhedra and their role in three-dimensional space. For example, the volume of an antiprism can be calculated using specific geometric formulas, making it a useful concept in various scientific and mathematical applications. |
3-Dimensional Figures |

|
Definition--Geometry Basics--Prism |
PrismTopicGeometry Basics DefinitionA prism is a solid shape with two parallel, congruent bases connected by rectangular or parallelogram faces. DescriptionPrisms are significant in the study of three-dimensional shapes. They have a uniform cross-section, allowing for easy calculations of volume and surface area. The volume can be calculated with the formula V = B⋅h where B is the area of the base and h is the height. Prisms are commonly encountered in real-world applications such as packaging and structural designs, making them an essential concept in geometry. |
3-Dimensional Figures |

|
Google Earth Voyager Story: Architectural Prisms, Part 3 |
Google Earth Voyager Story: Architectural Prisms, Part 3
In this Google Earth Voyager story visit architectural landmarks in New York City to learn about the geometry of prisms. In this lesson, visit the Freedom Tower in Lower Manhattan and learn about antiprisms. Then build a scale model of the Freedom Tower. This is part of a collection of Google Earth Voyager Stories that use Google's mapping technology to explore relevant math stories. To see the complete collection of the Google Earth Voyager Stories, click on this link. Note: The download is the teacher's guide.Viewing Media4Math Stories on Google EarthThese Google Earth Voyager Stories are also available on Google Earth. Best viewed in Chrome, click on the links below to view these dynamic stories using Google's technology: |
3-Dimensional Figures |

|
Holiday Math Clip Art--Candy Box |
Holiday Math Clip Art--Candy BoxTopicGeometry DescriptionThis holiday-themed math clip art features a festive candy box, offering a delightful blend of seasonal cheer and geometric concepts. The image can be broken down into its fundamental geometric components, showcasing both 2D and 3D elements. In 2D, the candy box presents a cardioid shape, resembling a heart or rounded triangle. This unique curve can be explored in terms of its properties and equations. The box's decorative elements, such as bows or patterns, may incorporate additional 2D shapes like circles, ovals, or polygons. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Holiday Math Clip Art--Candy Cane |
Holiday Math Clip Art--Candy CaneTopicGeometry Description
This holiday-themed math clip art showcases a classic candy cane, a perfect subject for exploring various geometric concepts. The candy cane's distinctive shape offers rich opportunities for analyzing both 2D and 3D geometric elements. In 2D, the candy cane can be broken down into rectangles and semicircles. The straight part of the cane forms a rectangle, while the curved hook at the top creates a semicircle. This allows for discussions about properties of these shapes, such as area calculations and the relationship between a semicircle's diameter and its arc length. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Holiday Math Clip Art--Candy Mint |
Holiday Math Clip Art--Candy Mint
This is part of a collection of math clip art images that take holiday images and render them as two- and three-dimensional geometric objects. To see the complete collection of these images, click on this link. Note: The download is a PNG file.Math Clip Art LibraryTo see the complete Math Clip Art Library, click on this link. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Holiday Math Clip Art--Chocolate Bar |
Holiday Math Clip Art--Chocolate Bar
This is part of a collection of math clip art images that take holiday images and render them as two- and three-dimensional geometric objects. To see the complete collection of these images, click on this link. Note: The download is a PNG file.Math Clip Art LibraryTo see the complete Math Clip Art Library, click on this link. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
3-Dimensional Figures and Applications of 3D Geometry |
|
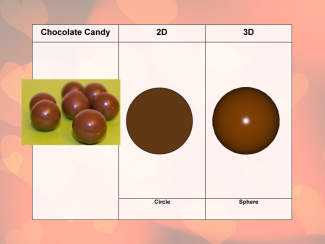
Holiday Math Clip Art--Chocolate Candy |
Holiday Math Clip Art--Chocolate CandyTopicGeometry DescriptionThis holiday-themed math clip art features chocolate candy, providing an excellent opportunity to explore geometric concepts in both 2D and 3D contexts. The simplicity of the candy's shape belies the rich mathematical discussions it can inspire. In 2D, the chocolate candy presents as a perfect circle. This allows for exploration of circular properties such as diameter, radius, circumference, and area. The candy's surface design, which may include patterns or decorations, can introduce concepts like symmetry, geometric transformations, or even basic trigonometry if the designs include angular elements. |
Size, 3-Dimensional Figures and Applications of 3D Geometry |

|
Holiday Math Clip Art--Christmas Tree |
Holiday Math Clip Art--Christmas TreeTopicGeometry DescriptionThis holiday-themed math clip art showcases a Christmas tree, offering a festive way to explore various geometric concepts in both 2D and 3D contexts. The tree's distinctive shape provides rich opportunities for mathematical analysis and discussion. In 2D, the Christmas tree can be broken down into a triangle for the main body and a rectangle for the trunk. This allows for exploration of properties such as angles, base, height, area, and perimeter. The decorations on the tree can introduce concepts of symmetry, patterns, and even coordinate geometry if we imagine the ornaments as points on a plane. |
3-Dimensional Figures and Applications of 3D Geometry |
|
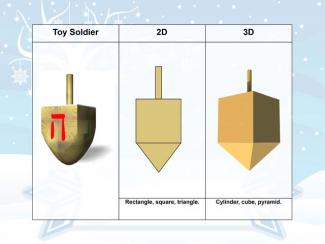
Holiday Math Clip Art--Dreidel |
Holiday Math Clip Art--DreidelTopicGeometry DescriptionThis holiday-themed math clip art features a dreidel, a traditional Hanukkah toy that offers a unique opportunity to explore geometric concepts in both 2D and 3D contexts. The dreidel's distinctive shape provides a rich foundation for various mathematical discussions. In 2D, the dreidel can be broken down into several shapes. The body presents as a square or rectangle, the top as a smaller rectangle, and the point at the bottom as a triangle. This allows for exploration of properties such as angles, sides, area, and perimeter. The Hebrew letters on each face introduce concepts of symmetry and rotational transformations. |
3-Dimensional Figures and Applications of 3D Geometry |
|
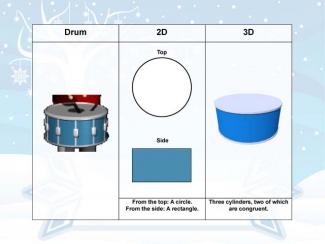
Holiday Math Clip Art--Drum |
Holiday Math Clip Art--DrumTopicGeometry DescriptionThis holiday-themed math clip art features a festive drum, offering an excellent opportunity to explore geometric concepts in both 2D and 3D contexts. The drum's simple yet distinctive shape provides a rich foundation for various mathematical discussions. In 2D, the drum can be broken down into basic shapes. The top and bottom of the drum present as circles, while the side forms a rectangle. This allows for exploration of properties such as diameter, radius, circumference, and area for circles, as well as length, width, and perimeter for rectangles. The decorative elements on the drum's surface can introduce concepts of symmetry and patterns. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Holiday Math Clip Art--Gift Box |
Holiday Math Clip Art--Gift Box
This is part of a collection of math clip art images that take holiday images and render them as two- and three-dimensional geometric objects. To see the complete collection of these images, click on this link. Note: The download is a PNG file.Math Clip Art LibraryTo see the complete Math Clip Art Library, click on this link. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
3-Dimensional Figures and Applications of 3D Geometry |
|
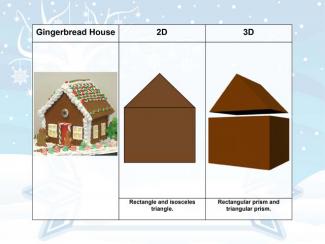
Holiday Math Clip Art--Gingerbread House |
Holiday Math Clip Art--Gingerbread HouseTopicGeometry DescriptionThis holiday-themed math clip art features a gingerbread house, offering a delightful way to explore geometric concepts in both 2D and 3D contexts. The gingerbread house's structure provides a rich foundation for various mathematical discussions, combining architectural elements with festive design. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Holiday Math Clip Art--Gingerbread Man |
Holiday Math Clip Art--Gingerbread ManTopicGeometry DescriptionThis holiday-themed math clip art showcases a gingerbread man, offering a festive way to explore geometric concepts in both 2D and 3D contexts. The gingerbread man's shape provides a unique opportunity to discuss various geometric forms and their combinations. |
3-Dimensional Figures and Applications of 3D Geometry |
|
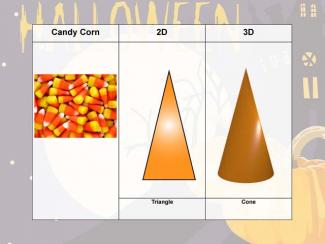
Holiday Math Clip Art--Halloween--Candy Corn |
Holiday Math Clip Art--Halloween--Candy CornTopicGeometry DescriptionThis Halloween-themed math clip art features candy corn, offering a seasonal way to explore geometric concepts in both 2D and 3D contexts. The distinctive shape of candy corn provides an excellent opportunity to discuss various geometric forms and their properties. In 2D, candy corn is typically represented as a triangle. This allows for exploration of properties such as angles, base, height, area, and perimeter. The three-color design of candy corn also introduces the concept of dividing a triangle into smaller triangles, which can lead to discussions about similarity and proportions. |
3-Dimensional Figures and Applications of 3D Geometry |
|
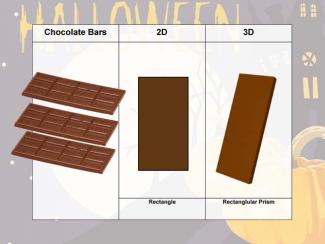
Holiday Math Clip Art--Halloween--Chocolate Bar |
Holiday Math Clip Art--Chocolate BarTopicGeometry DescriptionThis holiday-themed math clip art showcases a chocolate bar, offering a delightful way to explore geometric concepts in both 2D and 3D contexts. The chocolate bar's simple yet structured shape provides an excellent foundation for various mathematical discussions. In 2D, the chocolate bar presents as a rectangle. This allows for exploration of properties such as length, width, perimeter, and area. The individual chocolate squares within the bar create a grid, introducing concepts of arrays, rows, and columns. This grid structure can also be used to discuss fractions and ratios. |
3-Dimensional Figures and Applications of 3D Geometry |
|
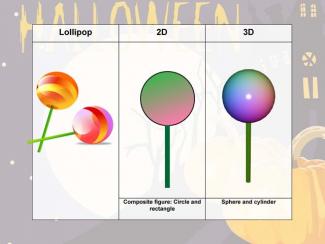
Holiday Math Clip Art--Halloween--Lollipop |
Holiday Math Clip Art--Halloween--LollipopTopicGeometry DescriptionThis Halloween-themed math clip art features a lollipop, offering a sweet way to explore geometric concepts in both 2D and 3D contexts. The lollipop's simple yet distinctive shape provides a rich foundation for various mathematical discussions. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Holiday Math Clip Art--Halloween--Mint |
Holiday Math Clip Art--Candy MintTopicGeometry DescriptionThis holiday-themed math clip art features a festive candy mint, providing an excellent opportunity to explore geometric concepts in both 2D and 3D contexts. The simplicity of the mint's shape belies the rich mathematical discussions it can inspire. In 2D, the candy mint presents as a perfect circle. This allows for exploration of circular properties such as diameter, radius, circumference, and area. The mint's surface design, often featuring spirals or radial patterns, can introduce concepts like rotational symmetry and geometric transformations. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Holiday Math Clip Art--Halloween--Moon |
Holiday Math Clip Art--Halloween--MoonTopicGeometry DescriptionThis Halloween-themed math clip art features a moon, offering a celestial way to explore geometric concepts in both 2D and 3D contexts. The moon's simple yet evocative shape provides a rich foundation for various mathematical discussions, particularly fitting for the spooky atmosphere of Halloween. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Holiday Math Clip Art--Halloween--Pumpkin |
Holiday Math Clip Art--Halloween--PumpkinTopicGeometry DescriptionThis Halloween-themed math clip art showcases a pumpkin, offering a festive way to explore geometric concepts in both 2D and 3D contexts. The pumpkin's distinctive shape provides a rich foundation for various mathematical discussions. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Holiday Math Clip Art--Halloween--Title Page |
Holiday Math Clip Art--Halloween--Title PageTopicGeometry DescriptionThis Halloween-themed math clip art features a title page, offering a spooky introduction to explore geometric concepts in both 2D and 3D contexts. While a title page might not immediately suggest geometric analysis, it provides an opportunity to discuss layout, design, and the geometric principles underlying visual communication. |
3-Dimensional Figures and Applications of 3D Geometry |
|
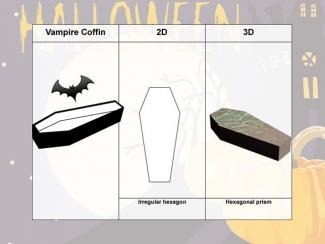
Holiday Math Clip Art--Halloween--Vampire Coffin |
Holiday Math Clip Art--Halloween--Vampire CoffinTopicGeometry DescriptionThis Halloween-themed math clip art features a vampire coffin, offering a spooky way to explore geometric concepts in both 2D and 3D contexts. The coffin's unique shape provides an excellent opportunity to discuss various geometric forms and their properties. |
3-Dimensional Figures and Applications of 3D Geometry |

|
Holiday Math Clip Art--Halloween--Witch's Hat |
Holiday Math Clip Art--Halloween--Witch's HatTopicGeometry DescriptionThis Halloween-themed math clip art features a witch's hat, offering a spooky way to explore geometric concepts in both 2D and 3D contexts. The distinctive shape of the witch's hat provides an excellent opportunity to discuss various geometric forms and their properties. |
3-Dimensional Figures and Applications of 3D Geometry |