
Illustrative Math Alignment: Grade 6 Unit 2
Introducing Ratios
Lesson 1: Introducing Ratios and Ratio Language
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topic |
|---|---|---|---|

|
Closed Captioned Video: Ratios and Proportions: Scale Drawings |
Closed Captioned Video: Ratios and Proportions: Scale DrawingsTopicRatios DescriptionThe video explains how proportions are used to create scale drawings, ensuring geometric figures remain proportional. Examples include finding dimensions in similar triangles, scaling architectural models, and solving geometric problems. The concept of proportional relationships is key to accurate scaling. |
Ratios and Rates |

|
Closed Captioned Video: Ratios and Proportions: Solving Proportions |
Closed Captioned Video: Ratios and Proportions: Solving ProportionsTopicRatios DescriptionThis video focuses on solving proportions algebraically, converting them into equations to solve real-world problems. Examples include predator-prey ratios, scaling pizza dough recipes, and creating shades of paint. The video demonstrates methods for handling terms in denominators and simplifying ratios to whole numbers. |
Ratios and Rates |

|
Closed Captioned Video: Ratios and Proportions: What Are Proportions? |
Closed Captioned Video: Ratios and Proportions: What Are Proportions?TopicRatios DescriptionProportions are explained as equivalent ratios used to solve real-world problems. Examples include matching juice mixtures and adjusting recipes. The video uses ratio tables and number lines to scale ratios proportionally in practical applications. |
Ratios and Rates |

|
Closed Captioned Video: Ratios and Rates: Converting Measurement Units |
Closed Captioned Video: Ratios and Rates: Converting Measurement UnitsTopicRatios DescriptionThis video covers converting units using rates, with examples like speed conversion, currency exchange, and calculating seconds in a year. It emphasizes multiplication by conversion rates to transition between units effectively. |
Ratios and Rates |

|
Closed Captioned Video: Ratios and Rates: Rates and Slopes of Lines |
Closed Captioned Video: Ratios and Rates: Rates and Slopes of LinesTopicRatios DescriptionRates are linked to slopes in linear functions. The video explores calculating rates of change for graphs of speed, savings growth, and loan repayment. It highlights using the slope formula to interpret and solve practical problems. |
Ratios and Rates |

|
Closed Captioned Video: Ratios and Rates: Rates from Data |
Closed Captioned Video: Ratios and Rates: Rates from DataTopicRatios DescriptionThis video demonstrates calculating rates from data sets, focusing on patterns like distance-time relationships and wages. Examples include determining car speeds, hourly wages, and unit costs of gasoline. Data tables are used to visualize and compute rates. |
Ratios and Rates |

|
Closed Captioned Video: Ratios and Rates: Ratios as Decimals |
Closed Captioned Video: Ratios and Rates: Ratios as DecimalsTopicRatios DescriptionThe video explores working with ratios involving decimals, such as finding unit costs for salmon or recycling rates. Scientific notation and multi-step conversions are used to calculate speeds of spacecraft like Voyager I. |
Ratios and Rates |

|
Closed Captioned Video: Ratios, Proportions, and Percents: Calculating Percents |
Closed Captioned Video: Ratios, Proportions, and Percents: Calculating PercentsTopicRatios DescriptionRatios are connected to percentages in this video. Examples include finding percentages of colored socks or non-green items in collections. It develops a formula for converting part-to-whole ratios into percentages. |
Ratios and Rates |

|
Closed Captioned Video: Ratios: Application of Ratios: Roofs and Ramps |
Closed Captioned Video: Ratios: Application of Ratios: Roofs and RampsTopicRatios DescriptionThe video covers practical applications of ratios for measuring slopes of roofs and ramps. Examples include comparing roof pitches, calculating base lengths of roofs, and determining ramp heights. Ratios provide clarity for gradual slopes. |
Ratios and Rates and Applications of Ratios, Proportions, and Percents |

|
Closed Captioned Video: Ratios: Equivalent Ratios |
Closed Captioned Video: Ratios: Equivalent RatiosTopicRatios DescriptionThis video explains generating and comparing equivalent ratios. Examples include simplifying fractions, determining similarity in geometric shapes, and integrating multiple ratios into a comprehensive ratio. Applications extend to geometry and proportional reasoning. |
Ratios and Rates |

|
Closed Captioned Video: Ratios: Fractional Ratios |
Closed Captioned Video: Ratios: Fractional RatiosTopicRatios DescriptionThis video focuses on ratios written with fractions, showing how to convert fractional ratios into whole-number ratios by eliminating denominators. Applications include recipes and ensuring proportions are maintained in measurements. It emphasizes mathematical manipulation to align ratios with practical uses. |
Ratios and Rates |

|
Closed Captioned Video: Ratios: Numerical Models for Ratios |
Closed Captioned Video: Ratios: Numerical Models for RatiosTopicRatios DescriptionNumerical methods for handling ratios are explored, such as double number lines and ratio tables. Examples include tropical punch recipes and fruit stand inventories. These methods simplify complex ratio calculations and are adaptable to various practical scenarios. |
Ratios and Rates |

|
Closed Captioned Video: Ratios: Rates |
Closed Captioned Video: Ratios: RatesTopicRatios DescriptionThis video introduces rates, a type of ratio comparing different units, such as distance over time (speed) or dollars per hour (wage). Examples demonstrate calculating rates and converting units. Applications include measuring efficiency and performing unit conversions. |
Ratios and Rates |

|
Closed Captioned Video: Ratios: Ratios and Fractions |
Closed Captioned Video: Ratios: Ratios and FractionsTopicRatios DescriptionRatios are compared to fractions, emphasizing differences between part-to-part and part-to-whole relationships. Examples include finding fractions of subsets within a collection and modeling classroom demographics. The video highlights deriving fractional equivalents from given ratios. |
Ratios and Rates |

|
Closed Captioned Video: Ratios: Ratios with Three Items |
Closed Captioned Video: Ratios: Ratios with Three ItemsTopicRatios DescriptionThe video explains ratios involving more than two items, such as 1:3:4, and how they encompass multiple pairwise ratios. Applications include recipes where ingredients are combined in specific proportions. It demonstrates working forward and backward with ratios to identify components or adjust quantities proportionally. |
Ratios and Rates |

|
Closed Captioned Video: Ratios: Unit Rates |
Closed Captioned Video: Ratios: Unit RatesTopicRatios DescriptionThe video focuses on unit rates, where the denominator equals one. It includes practical examples like finding the cost per pound of bananas or determining hourly wages. Applications extend to conversions and scaling calculations for various real-world tasks. |
Ratios and Rates |

|
Closed Captioned Video: Ratios: Visual Models for Ratios |
Closed Captioned Video: Ratios: Visual Models for RatiosTopicRatios DescriptionThe video showcases visual representations like tape diagrams, snap cubes, and grids to solve ratio problems. It includes examples such as determining quantities in coin collections and paint mixtures. Applications involve modeling real-world problems using clear, visual methods. |
Ratios and Rates |

|
Closed Captioned Video: Ratios: Visual Models for Ratios and Percents |
Closed Captioned Video: Ratios: Visual Models for Ratios and PercentsTopicRatios DescriptionThis video illustrates converting ratios to percents using visual aids like area models and grids. Examples include determining percentages of colored eggs, fruit types, and combinations of colored lights. |
Ratios and Rates |

|
Closed Captioned Video: Ratios: What Are Ratios? |
Closed Captioned Video: Ratios: What Are Ratios?TopicRatios DescriptionThis video introduces the concept of ratios, which describe relationships between quantities. Key concepts include writing ratios in different forms (e.g., 2:3, 2/3, and 2 to 3) and simplifying ratios. It also covers part-to-part ratios and part-to-whole ratios using examples like sports balls and colored shapes. Applications include categorizing objects and exploring numerical relationships in sets. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Converting Units |
Converting UnitsTopicRatios, Proportions, and Percents DefinitionConverting units involves changing a measurement from one unit to another using a conversion factor. DescriptionConverting units is essential in various fields such as science, engineering, and everyday life. It involves using ratios and proportions to switch between different measurement systems, such as converting inches to centimeters or gallons to liters. For example, to convert 5 miles to kilometers, knowing that 1 mile is approximately 1.60934 kilometers, you multiply 5 × 1.60934 = 8.0467 kilometers |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Equivalent Ratios |
Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionEquivalent ratios are ratios that express the same relationship between quantities. DescriptionEquivalent ratios are fundamental in understanding proportions and scaling in mathematics. They represent the same relationship between quantities, even though the numbers themselves may differ. This concept is crucial in various applications, such as cooking, map reading, and creating models. For instance, the ratios 2:3 and 4:6 are equivalent because they both simplify to the same ratio when reduced. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Part Ratios |
Part-to-Part RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-part ratios compare different parts of a whole to each other. DescriptionPart-to-part ratios are used to compare different parts of a whole, providing a way to understand the relationship between different components. This type of ratio is essential in fields such as statistics, biology, and economics. For example, if a class has 10 boys and 15 girls, the part-to-part ratio of boys to girls is 10:15, which simplifies to 2:3. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Part-to-Whole Ratios |
Part-to-Whole RatiosTopicRatios, Proportions, and Percents DefinitionPart-to-whole ratios compare one part of a whole to the entire whole. These ratios are more commonly known as fractions. DescriptionPart-to-whole ratios are used to compare a part of a whole to the entire whole, providing insights into the composition of a dataset or population. This type of ratio, more commonly referred to as fractions, is widely used in statistics, finance, and everyday decision-making. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Rate |
RateTopicRatios, Proportions, and Percents DefinitionA rate is a ratio that compares two quantities with different units. DescriptionRates are used to compare different quantities, such as speed (miles per hour) or price (cost per item). Understanding rates is essential for interpreting data and making informed decisions in various contexts, such as travel and budgeting. For instance, if a car travels 60 miles in 2 hours, the rate is 30 miles per hour. Learning about rates helps students analyze real-world situations and apply mathematical reasoning to everyday problems. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratio |
RatioTopicRatios, Proportions, and Percents DefinitionA ratio is a comparison of two quantities by division. DescriptionRatios are used to express the relationship between two quantities, providing a way to compare different amounts. They are fundamental in various fields, including mathematics, science, and finance. For example, the ratio of 4 to 5 can be written as 4:5 or 4/5. Understanding ratios helps students analyze data, solve problems, and make informed decisions in real-world situations. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Fractions |
Ratios and FractionsTopicRatios, Proportions, and Percents DefinitionRatios and fractions are both ways of comparing quantities, with fractions representing a part of a whole. DescriptionUnderstanding the connection between ratios and fractions is crucial for solving problems involving proportions and scaling. Ratios can be expressed as fractions, providing a way to understand the relationship between quantities. A fraction is a part-whole ratio. |
Ratios and Rates |
|
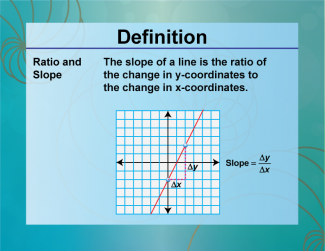
Definition--Ratios, Proportions, and Percents Concepts--Ratios and Slope |
Ratios and SlopeTopicRatios, Proportions, and Percents DefinitionThe slope of a line is a ratio that represents the change in y over the change in x. DescriptionUnderstanding the relationship between ratios and slope is essential for interpreting graphs and solving problems in algebra and geometry. The slope is a measure of how steep a line is, calculated as the ratio of the vertical change to the horizontal change between two points. For example, if a line rises 2 units for every 3 units it runs horizontally, the slope is 2/3. This concept is crucial for understanding linear relationships and analyzing data in various fields. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Decimals |
Ratios with DecimalsTopicRatios, Proportions, and Percents DefinitionRatios with decimals involve comparing two quantities where one or both of the quantities are represented as decimal numbers. DescriptionRatios with decimals are crucial in various real-world applications, particularly in financial calculations, engineering, and scientific measurements. For instance, when calculating financial ratios such as the price-to-earnings ratio, decimals are often involved. Understanding how to work with these ratios allows for more precise and meaningful comparisons. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Fractions |
Ratios with FractionsTopicRatios, Proportions, and Percents DefinitionRatios with fractions compare two quantities where one or both of the quantities are fractions. DescriptionRatios with fractions are essential in various mathematical and real-world contexts, such as cooking, where ingredients are often measured in fractions. Understanding these ratios allows for accurate scaling of recipes or other measurements. For example, if a recipe calls for 1/2 cup of sugar to 1/4 cup of butter, the ratio is 1/2:1/4, which simplifies to 2:1 by multiplying both terms by 4. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Ratios with Percents |
Ratios with PercentsTopicRatios, Proportions, and Percents DefinitionRatios with percents involve comparing quantities where one or both of the quantities are expressed as percentages. DescriptionRatios with percents are widely used in various fields, including finance, statistics, and everyday life. For example, when comparing interest rates, growth rates, or discount rates, percentages are often used. Understanding these ratios allows for better financial decision-making and data analysis. |
Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--The Golden Ratio |
The Golden RatioTopicRatios, Proportions, and Percents DefinitionThe Golden Ratio is a special number approximately equal to 1.618, often denoted by the Greek letter φ (phi), which appears in various aspects of art, architecture, and nature. |
Applications of Ratios, Proportions, and Percents and Ratios and Rates |

|
Definition--Ratios, Proportions, and Percents Concepts--Unit Rate |
Unit RateTopicRatios, Proportions, and Percents DefinitionA unit rate is a comparison of any two separate but related measurements when one of the measurements is reduced to a single unit. DescriptionUnit rates are commonly used in everyday life, such as calculating speed (miles per hour), cost per item, or efficiency (miles per gallon). For example, if a car travels 300 miles on 10 gallons of gas, the unit rate is 30 miles per gallon. |
Ratios and Rates |
|
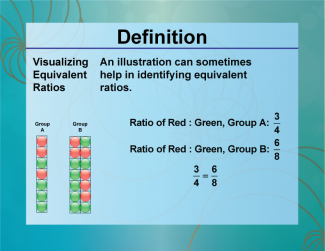
Definition--Ratios, Proportions, and Percents Concepts--Visualizing Equivalent Ratios |
Visualizing Equivalent RatiosTopicRatios, Proportions, and Percents DefinitionVisualizing equivalent ratios involves using diagrams or models to show that two ratios are equivalent. DescriptionVisualizing equivalent ratios is important in fields such as mathematics and engineering, where understanding proportional relationships is crucial. For example, using a double number line or a ratio table can help illustrate that the ratios 2:3 and 4:6 are equivalent. |
Ratios and Rates |
|
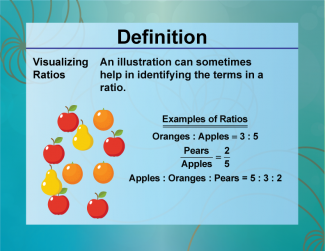
Definition--Ratios, Proportions, and Percents Concepts--Visualizing Ratios |
Visualizing RatiosTopicRatios, Proportions, and Percents DefinitionVisualizing ratios involves using diagrams or models to represent and understand the relationship between two quantities. DescriptionVisualizing ratios is essential in various fields, such as mathematics, science, and economics, where understanding the relationship between quantities is crucial. For example, using a bar model or a double number line can help illustrate the ratio of 3:4. |
Ratios and Rates |

|
Desmos Activity: Slope As Rate of Change |
Desmos Activity: Slope As Rate of Change Use this activity to explore slope as a rate of change. In this Desmos activity, the slope of the line is the rate (cost per pound) for purchasing fruit. Students manipulate the slider for m to see the impact on the cost. |
Slope and Ratios and Rates |

|
Formulas--Converting Celsius to Fahrenheit |
Formulas--Converting Celsius to Fahrenheit
The formula for the Converting Celsius to Fahrenheit. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Formulas--Converting Days to Hours |
Formulas--Converting Days to Hours
The formula for Converting Days to Hours. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Formulas--Converting Days to Minutes |
Formulas--Converting Days to Minutes
The formula for Converting Days to Minutes. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Formulas--Converting Days to Seconds |
Formulas--Converting Days to Seconds
The formula for Converting Days to Seconds. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Formulas--Converting Degrees to Radians |
Formulas--Converting Degrees to Radians
The formula for Converting Degrees to Radians. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Formulas--Converting Fahrenheit to Celsius |
Formulas--Converting Fahrenheit to Celsius
The formula for Converting Fahrenheit to Celsius. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Formulas--Converting Hours to Minutes |
Formulas--Converting Hours to Minutes
The formula for Converting Hours to Minutes. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Formulas--Converting Hours to Seconds |
Formulas--Converting Hours to Seconds
The formula for Converting Hours to Seconds. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Formulas--Converting Minutes to Seconds |
Formulas--Converting Minutes to Seconds
The formula for Converting Minutes to Seconds. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Formulas--Converting Radians to Degrees |
Formulas--Converting Radians to Degrees
The formula for Converting Radians to Degrees. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Formulas--Converting Seconds to Days |
Formulas--Converting Seconds to Days
The formula for Converting Seconds to Days. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Formulas--Converting Seconds to Hours |
Formulas--Converting Seconds to Hours
The formula for Converting Seconds to Hours. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Formulas--Converting Seconds to Minutes |
Formulas--Converting Seconds to Minutes
The formula for Converting Seconds to Minutes. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Applications of Ratios, Proportions, and Percents, Proportions and Ratios and Rates |

|
Instructional Resource--Fibonacci Sequence, Lesson 4 |
Instructional Resource | Fibonacci Sequence, Lesson 4
This is a continuation of our exploration of the Fibonacci Sequence. In this lesson we look at the Golden Ratio phi. —PRESS PREVIEW TO VIEW THE LESSON— To see the other lessons in this series, click on the link.Note: The download is a PDF file. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Sequences, Ratios and Rates and Proportions |

|
Instructional Resource--Fibonacci Sequence, Lesson 5 |
Instructional Resource | Fibonacci Sequence, Lesson 5
This is a continuation of our exploration of the Fibonacci Sequence. In this lesson we look at the Golden Ratio phi. —PRESS PREVIEW TO VIEW THE LESSON— To see the other lessons in this series, click on the link.Note: The download is a PDF file. Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Sequences, Ratios and Rates and Proportions |