Illustrative Math Alignment: Grade 6 Unit 3

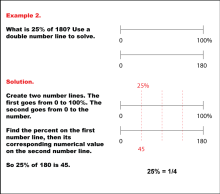
Topic

Ratios, Proportions, Percents

Description

This example illustrates how to calculate 25% of 180 using a double number line. The solution presents two parallel number lines: one spanning from 0 to 100% and the other from 0 to 180. By aligning 25% on the percentage line with its corresponding value on the numerical line, we can determine that 25% of 180 is 45. This method visually demonstrates that 25% is equivalent to one-quarter of a quantity.

Topic

Ratios, Proportions, Percents

Description

This example demonstrates how to find 33 1/3% of 240 using a double number line. The solution displays two parallel number lines: one ranging from 0 to 100% and the other from 0 to 240. By aligning 33 1/3% on the percentage line with its corresponding value on the numerical line, we can see that 33 1/3% of 240 is 80. This method visually represents the concept that 33 1/3% is equivalent to one-third of a quantity.

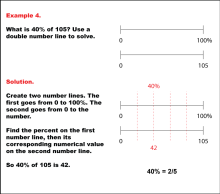
Topic

Ratios, Proportions, Percents

Description

This example illustrates how to calculate 40% of 105 using a double number line. The solution presents two parallel number lines: one spanning from 0 to 100% and the other from 0 to 105. By aligning 40% on the percentage line with its corresponding value on the numerical line, we can determine that 40% of 105 is 42. This method visually demonstrates that 40% is equivalent to two-fifths of a quantity.

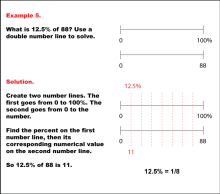
Topic

Ratios, Proportions, Percents

Description

This example demonstrates how to find 12.5% of 88 using a double number line. The solution shows two parallel number lines: one ranging from 0 to 100% and the other from 0 to 88. By aligning 12.5% on the percentage line with its corresponding value on the numerical line, we can see that 12.5% of 88 is 11. This method visually represents the concept that 12.5% is equivalent to one-eighth of a quantity.

Topic

Ratios, Proportions, Percents

Description

This example demonstrates how to solve for an unknown value using a double number line when given a percentage. The image features two parallel number lines: one ranging from 0 to 100% and another from 0 to an unknown value x. It visually illustrates the process of determining x when 75 is 50% of x.

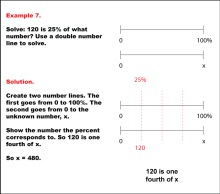
Topic

Ratios, Proportions, Percents

Description

This example illustrates how to determine an unknown value using a double number line when given a part and its corresponding percentage. The image depicts two parallel number lines: one spanning from 0 to 100% and another from 0 to an unknown value x. It visually demonstrates the process of finding x when 120 is 25% of x.

Topic

Ratios, Proportions, Percents

Description

This example demonstrates how to find an unknown value using a double number line when given a part and its corresponding percentage, involving a fractional percentage. The image shows two parallel number lines: one ranging from 0 to 100% and another from 0 to an unknown value x. It visually illustrates the process of determining x when 125 is 33 1/3% of x.

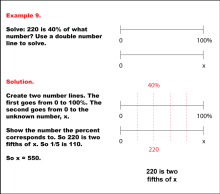
Topic

Ratios, Proportions, Percents

Description

This example illustrates how to solve for an unknown value using a double number line when given a part and its corresponding percentage. The image shows two horizontal number lines: the top line ranges from 0 to 100%, and the bottom line ranges from 0 to an unknown number x. The 40% mark on the top line aligns with 220 on the bottom line, visually demonstrating the process of finding x when 220 is 40% of x.

Topic

Ratios

Description

This example demonstrates the use of double number lines to solve a ratio problem involving orange and lemon juice. The juice mixture uses a ratio of 2 parts orange juice to 1 part lemon juice. Given 6 cups of orange juice, students are asked to determine the amount of lemon juice needed. The solution involves aligning the double number lines at the amount of orange juice and reading the corresponding amount of lemon juice, which is 3 cups.

Topic

Ratios

Description

This example introduces a four-part ratio of 5:2:1:1 for orange, lemon, lime, and strawberry juice. Given 10 cups of orange juice, students need to determine the amounts of lemon, lime, and strawberry juice required. The solution shows that 4 cups of lemon juice and 2 cups each of lime and strawberry juice are needed to maintain the ratio.

Topic

Ratios

Description

This example builds upon the previous one, using the same ratio of 2 parts orange juice to 1 part lemon juice. However, in this case, students are given 4 cups of lemon juice and asked to determine the amount of orange juice needed. The solution involves aligning the double number lines at the amount of lemon juice and reading the corresponding amount of orange juice, which is 8 cups.

Topic

Ratios

Description

This example introduces a new ratio of 3 parts orange juice to 1 part lime juice. Students are given 9 cups of orange juice and asked to determine the amount of lime juice needed. The solution involves using a double number line to align at the amount of orange juice and find the corresponding amount of lime juice, which is 3 cups.

Topic

Ratios

Description

This example introduces a more complex ratio of 3 parts orange juice to 2 parts lime juice. Students are given 4 cups of lime juice and asked to determine the amount of orange juice needed. The solution involves using a double number line to align at the amount of lime juice and find the corresponding amount of orange juice, which is 6 cups.

Topic

Ratios

Description

This example introduces a three-part ratio of 2:1:1 for orange, lemon, and raspberry juice. Given 4 cups of orange juice, students need to determine the amounts of lemon and raspberry juice required. The solution shows that 2 cups each of lemon and raspberry juice are needed to maintain the ratio.

Topic

Ratios

Description

This example presents a three-part ratio of 3:2:2 for orange, lemon, and raspberry juice. Given 6 cups of lemon juice, students need to determine the amounts of orange and raspberry juice required. The solution shows that 9 cups of orange juice and 6 cups of raspberry juice are needed to maintain the ratio.

This is part of a series of math examples that show how to solve ratio problems involving double number lines.

Note: The download is a PNG file.

Topic

Ratios

Description

This example presents a three-part ratio of 4:3:2 for orange, lemon, and lime juice. Given 4 cups of lime juice, students need to determine the amounts of orange and lemon juice required. The solution shows that 8 cups of orange juice and 6 cups of lemon juice are needed to maintain the ratio.

Topic

Ratios

Description

This example features a three-part ratio of 5:2:1 for orange, lemon, and lime juice. Given 6 cups of lemon juice, students need to determine the amounts of orange and lime juice required. The solution demonstrates that 15 cups of orange juice and 3 cups of lime juice are needed to maintain the ratio.

What Are Percents?

July 2014. In this issue of Math in the News we look at the mathematics of the Nielsen Ratings. This provides an excellent application of ratios, proportions, and percents.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

8/8/11. In this issue we look at federal spending and the growth of such spending. Looking at data provided by the government, we calculate the annual rate of growth.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

July 2015. This edition of Math in the News focuses on the severe drought currently taking place in California, and how it has impacted the water resources available to the state. In this edition, students will see how to use percentages given to determine actual amounts, and to determine percents out of a whole.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

July 2015. This edition of Math in the News focuses on the severe drought currently taking place in California, and how it has impacted the water resources available to the state. In this edition, students will see how to use percentages given to determine actual amounts, and to determine percents out of a whole.

Related Resources

To see resources related to this topic click on the Related Resources tab above.

This is part of a collection of math quizzes on the topic of Equations with Percents.

Related Resources

Quiz Library

ary">click on this link.

This is part of a collection of math quizzes on the topic of Equations with Percents.

Related Resources

Quiz Library

ary">click on this link.

This is part of a collection of math quizzes on the topic of Equations with Percents.

Related Resources

Quiz Library

ary">click on this link.

This 45-minute SAT Math prep lesson focuses on ratios, proportions, and percents—key concepts that appear throughout the Problem Solving and Data Analysis domain of the SAT. These topics account for approximately 29% of the SAT Math section and often appear in real-world scenarios involving recipes, maps, discounts, and data comparisons. In this lesson, students will learn to simplify ratios, solve proportions using cross multiplication, calculate percent increase and decrease, and solve percent-based equations involving unknowns.

This 45-minute SAT Math lesson focuses on mastering percents, percent increase and decrease, percent error, and reverse percent problems. Students will learn to convert between fractions, decimals, and percents, and apply key percent formulas to real-world and test-style problems. The lesson includes a warm-up activity, five instructional examples, a five-problem review section, and a 10-question SAT-style quiz with detailed solutions. Students also learn how to recognize percent-related language on the SAT and determine the correct solving strategy.

Topic

Fractions

Description

The term Percent represents a fraction with a denominator of 100, showing a proportion out of 100. Examples include 1% = 1/100, 5% = 5/100, and 25% = 25/100. Percentages are a real-world application of fractions and decimals, often used in data analysis, finance, and everyday calculations.

Topic

Fractions

Description

The term Percent Error describes the difference between an estimated value and the actual value, expressed as a percentage of the actual value. The example provided shows an estimated value of 100 versus an actual value of 107, resulting in a percent error of approximately 6.54%. This concept links fractions, percentages, and error analysis, which are important in measurement and data accuracy.

Topic

Fractions

Description

The term Percentage refers to converting fractions and decimals into their equivalent percentages. Examples include 1/2 = 50%, 0.4 = 40%, and 1/3 ≈ 33.3%. This concept connects fractions, decimals, and percentages, emphasizing their equivalence and usage in various contexts.

Topic

Fractions

Description

The term Percentage Decrease refers to the reduction in value expressed as a percentage of the original value. The example shows a decrease from 75 to 50, calculated as (75 - 50) / 75 * 100%, which equals 33.3%. This term applies percentages to real-world contexts like discounts and data analysis, building on fraction concepts.

Topic

Fractions

Description

The term Percentage Increase refers to the increase in value expressed as a percentage of the original value. The example shows an increase from 25 to 40, calculated as (40 - 25) / 25 * 100%, which equals 60%. This term reinforces the application of percentages and fractions in scenarios like profit and growth analysis.

What Are Ratios?

A ratio is the relationship between two or more quantities among a group of items.

This is the transcript that goes with the video segment entitled Video: Percents: Applications of Percent -- Grade.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.

This is the transcript that goes with the video segment entitled Video: Percents: Calculating Commissions and Tips.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.

This is the transcript that goes with the video segment entitled Video: Percents: Calculating Tax.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.

This is the transcript that goes with the video segment entitled Video: Percents: Calculating the Whole Given a Percent.

To see the complete collection of video transcriptsy, click on this link.

This is the transcript that goes with the video segment entitled Video: Percents: Estimating Percents.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.

This is the transcript that goes with the video segment entitled Video: Percents: Fraction-Percent Conversion.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.

This is the transcript that goes with the video segment entitled Video: Percents: Multiple Percents.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.

This is the transcript that goes with the video segment entitled Video: Percents: Percent Decrease.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.

This is the transcript that goes with the video segment entitled Video: Percents: Percent Increase.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.

This is the transcript that goes with the video segment entitled Video Tutorial: Percents: Percent of a Difference.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.

This is the transcript that goes with the video segment entitled Video Tutorial: Percents: Percent of a Number.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.

This is the transcript that goes with the video segment entitled Video Tutorial: Percents: Percents and Multiples of Numbers.

To see the complete collection of video transcriptsy, click on this link.

This is the transcript that goes with the video segment entitled Video Tutorial: Percents: Probabilities and Percents.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.

This is the transcript that goes with the video segment entitled Video Tutorial: Percents: Simple Interest.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.

This is the transcript that goes with the video segment entitled Video Tutorial: Percents: The Percent One Number is of Another.

To see the complete collection of video transcriptsy, click on this link.

This is the transcript that goes with the video segment entitled Video Tutorial: Percents: Visual Models for Percents.

To see the complete collection of video transcriptsy, click on this link.

To see the complete collection of videos in the Video Library, click on this link.