
Illustrative Math Alignment: Grade 6 Unit 1
Dividing Fractions
Lesson 15: Volume of Prisms
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Middle School Geometry—Grade 6—Lesson 2: Volume of Rectangular Prisms | Middle School Geometry--Grade 6--Lesson 2: Volume of Rectangular Prisms This standards-aligned lesson introduces students to the concept of volume through the lens of rectangular prisms. Designed for Grade 6 learners, the lesson builds on students’ understanding of area and extends it into three dimensions using the volume formulas V=l×w×h and V=B×h. Students engage with real-world problems, including a featured exploration of the 432 Park Avenue building in New York City, modeled as a rectangular prism. Through guided instruction, they learn to calculate volume using both whole numbers and fractional edge lengths, reinforcing fluency with multiplication, decimals, and spatial reasoning. |
Rectangular Prisms |

|
Middle School Geometry—Grade 6—Lesson 2: Volume of Rectangular Prisms | Middle School Geometry--Grade 6--Lesson 2: Volume of Rectangular Prisms This standards-aligned lesson introduces students to the concept of volume through the lens of rectangular prisms. Designed for Grade 6 learners, the lesson builds on students’ understanding of area and extends it into three dimensions using the volume formulas V=l×w×h and V=B×h. Students engage with real-world problems, including a featured exploration of the 432 Park Avenue building in New York City, modeled as a rectangular prism. Through guided instruction, they learn to calculate volume using both whole numbers and fractional edge lengths, reinforcing fluency with multiplication, decimals, and spatial reasoning. |
Rectangular Prisms |

|
Video Definition 59--3D Geometry--Volume--Spanish Audio | Video Definition 59--3D Geometry--Volume--Spanish Audio This is part of a collection of math video definitions related to the topic of 3D Geometry. These videos have Spanish audio. Note: The download is an MP4 video. |
Volume |

|
Video Definition 59--3D Geometry--Volume--Spanish Audio | Video Definition 59--3D Geometry--Volume--Spanish Audio This is part of a collection of math video definitions related to the topic of 3D Geometry. These videos have Spanish audio. Note: The download is an MP4 video. |
Volume |

|
Video Definition 59--3D Geometry--Volume--Spanish Audio | Video Definition 59--3D Geometry--Volume--Spanish Audio This is part of a collection of math video definitions related to the topic of 3D Geometry. These videos have Spanish audio. Note: The download is an MP4 video. |
Volume |

|
Video Definition 59--3D Geometry--Volume--Spanish Audio | Video Definition 59--3D Geometry--Volume--Spanish Audio This is part of a collection of math video definitions related to the topic of 3D Geometry. These videos have Spanish audio. Note: The download is an MP4 video. |
Volume |

|
Video Definition 59--3D Geometry--Volume | VolumeTopic3D Geometry DefinitionVolume is the amount of space occupied by a three-dimensional object. DescriptionVolume is a fundamental concept in geometry, representing the amount of space a three-dimensional object occupies. It is essential for calculating the capacity of containers, the displacement of fluids, and the mass of objects. Understanding volume involves using formulas specific to each shape, such as V = l × w × h for a rectangular prism or V = 4/3 πr3 |
Volume |

|
Video Definition 59--3D Geometry--Volume | VolumeTopic3D Geometry DefinitionVolume is the amount of space occupied by a three-dimensional object. DescriptionVolume is a fundamental concept in geometry, representing the amount of space a three-dimensional object occupies. It is essential for calculating the capacity of containers, the displacement of fluids, and the mass of objects. Understanding volume involves using formulas specific to each shape, such as V = l × w × h for a rectangular prism or V = 4/3 πr3 |
Volume |

|
Video Definition 59--3D Geometry--Volume | VolumeTopic3D Geometry DefinitionVolume is the amount of space occupied by a three-dimensional object. DescriptionVolume is a fundamental concept in geometry, representing the amount of space a three-dimensional object occupies. It is essential for calculating the capacity of containers, the displacement of fluids, and the mass of objects. Understanding volume involves using formulas specific to each shape, such as V = l × w × h for a rectangular prism or V = 4/3 πr3 |
Volume |

|
Video Definition 59--3D Geometry--Volume | VolumeTopic3D Geometry DefinitionVolume is the amount of space occupied by a three-dimensional object. DescriptionVolume is a fundamental concept in geometry, representing the amount of space a three-dimensional object occupies. It is essential for calculating the capacity of containers, the displacement of fluids, and the mass of objects. Understanding volume involves using formulas specific to each shape, such as V = l × w × h for a rectangular prism or V = 4/3 πr3 |
Volume |
|
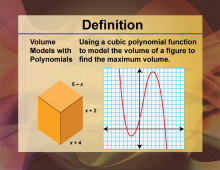
Video Definition 23--Polynomial Concepts--Volume Models with Polynomials (Spanish Audio) | Video Definition 23--Polynomial Concepts--Volume Models with Polynomials (Spanish Audio)
TopicPolynomials DescriptionVolume Models with Polynomials: Using a cubic polynomial function to model the volume of a figure to find the maximum volume. Example involves a rectangular prism with dimensions x + 2, x + 4, and 5 - x, leading to a cubic equation. Extends the application of polynomials to geometric optimization problems. |
Polynomial Expressions |

|
Video Definition 23--Polynomial Concepts--Volume Models with Polynomials (Spanish Audio) | Video Definition 23--Polynomial Concepts--Volume Models with Polynomials (Spanish Audio)
TopicPolynomials DescriptionVolume Models with Polynomials: Using a cubic polynomial function to model the volume of a figure to find the maximum volume. Example involves a rectangular prism with dimensions x + 2, x + 4, and 5 - x, leading to a cubic equation. Extends the application of polynomials to geometric optimization problems. |
Polynomial Expressions |

|
Video Definition 23--Polynomial Concepts--Volume Models with Polynomials (Spanish Audio) | Video Definition 23--Polynomial Concepts--Volume Models with Polynomials (Spanish Audio)
TopicPolynomials DescriptionVolume Models with Polynomials: Using a cubic polynomial function to model the volume of a figure to find the maximum volume. Example involves a rectangular prism with dimensions x + 2, x + 4, and 5 - x, leading to a cubic equation. Extends the application of polynomials to geometric optimization problems. |
Polynomial Expressions |

|
Video Definition 23--Polynomial Concepts--Volume Models with Polynomials (Spanish Audio) | Video Definition 23--Polynomial Concepts--Volume Models with Polynomials (Spanish Audio)
TopicPolynomials DescriptionVolume Models with Polynomials: Using a cubic polynomial function to model the volume of a figure to find the maximum volume. Example involves a rectangular prism with dimensions x + 2, x + 4, and 5 - x, leading to a cubic equation. Extends the application of polynomials to geometric optimization problems. |
Polynomial Expressions |

|
Video Definition 23--Polynomial Concepts--Volume Models with Polynomials | Video Definition 23--Polynomial Concepts--Volume Models with Polynomials
TopicPolynomials DescriptionVolume Models with Polynomials: Using a cubic polynomial function to model the volume of a figure to find the maximum volume. Example involves a rectangular prism with dimensions x + 2, x + 4, and 5 - x, leading to a cubic equation. Extends the application of polynomials to geometric optimization problems. |
Polynomial Expressions |

|
Video Definition 23--Polynomial Concepts--Volume Models with Polynomials | Video Definition 23--Polynomial Concepts--Volume Models with Polynomials
TopicPolynomials DescriptionVolume Models with Polynomials: Using a cubic polynomial function to model the volume of a figure to find the maximum volume. Example involves a rectangular prism with dimensions x + 2, x + 4, and 5 - x, leading to a cubic equation. Extends the application of polynomials to geometric optimization problems. |
Polynomial Expressions |

|
Video Definition 23--Polynomial Concepts--Volume Models with Polynomials | Video Definition 23--Polynomial Concepts--Volume Models with Polynomials
TopicPolynomials DescriptionVolume Models with Polynomials: Using a cubic polynomial function to model the volume of a figure to find the maximum volume. Example involves a rectangular prism with dimensions x + 2, x + 4, and 5 - x, leading to a cubic equation. Extends the application of polynomials to geometric optimization problems. |
Polynomial Expressions |

|
Video Definition 23--Polynomial Concepts--Volume Models with Polynomials | Video Definition 23--Polynomial Concepts--Volume Models with Polynomials
TopicPolynomials DescriptionVolume Models with Polynomials: Using a cubic polynomial function to model the volume of a figure to find the maximum volume. Example involves a rectangular prism with dimensions x + 2, x + 4, and 5 - x, leading to a cubic equation. Extends the application of polynomials to geometric optimization problems. |
Polynomial Expressions |

|
Definition--Polynomial Concepts--Volume Models with Polynomials | Volume Models with PolynomialsTopicPolynomials DefinitionVolume models with polynomials involve using polynomial expressions to represent the volume of three-dimensional geometric shapes. DescriptionPolynomials play a significant role in various fields of mathematics and applied sciences. In the context of volume models, polynomials are used to represent the dimensions and volume of geometric shapes. For instance, the volume of a rectangular prism can be expressed as a polynomial where the length, width, and height are variables. This allows for a flexible and powerful way to model and solve real-world problems involving three-dimensional spaces. |
Polynomial Expressions |

|
Definition--Polynomial Concepts--Volume Models with Polynomials | Volume Models with PolynomialsTopicPolynomials DefinitionVolume models with polynomials involve using polynomial expressions to represent the volume of three-dimensional geometric shapes. DescriptionPolynomials play a significant role in various fields of mathematics and applied sciences. In the context of volume models, polynomials are used to represent the dimensions and volume of geometric shapes. For instance, the volume of a rectangular prism can be expressed as a polynomial where the length, width, and height are variables. This allows for a flexible and powerful way to model and solve real-world problems involving three-dimensional spaces. |
Polynomial Expressions |

|
Definition--Polynomial Concepts--Volume Models with Polynomials | Volume Models with PolynomialsTopicPolynomials DefinitionVolume models with polynomials involve using polynomial expressions to represent the volume of three-dimensional geometric shapes. DescriptionPolynomials play a significant role in various fields of mathematics and applied sciences. In the context of volume models, polynomials are used to represent the dimensions and volume of geometric shapes. For instance, the volume of a rectangular prism can be expressed as a polynomial where the length, width, and height are variables. This allows for a flexible and powerful way to model and solve real-world problems involving three-dimensional spaces. |
Polynomial Expressions |

|
Definition--Polynomial Concepts--Volume Models with Polynomials | Volume Models with PolynomialsTopicPolynomials DefinitionVolume models with polynomials involve using polynomial expressions to represent the volume of three-dimensional geometric shapes. DescriptionPolynomials play a significant role in various fields of mathematics and applied sciences. In the context of volume models, polynomials are used to represent the dimensions and volume of geometric shapes. For instance, the volume of a rectangular prism can be expressed as a polynomial where the length, width, and height are variables. This allows for a flexible and powerful way to model and solve real-world problems involving three-dimensional spaces. |
Polynomial Expressions |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 3 | Closed Captioned Video: Geometry Applications: Area and Volume, 3TopicArea and Volume DescriptionThis segment explores the surface area-to-volume ratio using the Citigroup Building as an example. It discusses how this ratio impacts energy efficiency in buildings and compares it to natural examples like polar bears and snakes for context. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 3 | Closed Captioned Video: Geometry Applications: Area and Volume, 3TopicArea and Volume DescriptionThis segment explores the surface area-to-volume ratio using the Citigroup Building as an example. It discusses how this ratio impacts energy efficiency in buildings and compares it to natural examples like polar bears and snakes for context. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 1 | Closed Captioned Video: Geometry Applications: Area and Volume, 1TopicArea and Volume DescriptionThis segment explores the concept of density, using the Titanic to demonstrate buoyancy and the relationship between mass and volume. It introduces direct variation, rational functions, and how these principles apply to ship design for optimal floating capacity. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 1 | Closed Captioned Video: Geometry Applications: Area and Volume, 1TopicArea and Volume DescriptionThis segment explores the concept of density, using the Titanic to demonstrate buoyancy and the relationship between mass and volume. It introduces direct variation, rational functions, and how these principles apply to ship design for optimal floating capacity. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 1 | Closed Captioned Video: Geometry Applications: Area and Volume, 1TopicArea and Volume DescriptionThis segment explores the concept of density, using the Titanic to demonstrate buoyancy and the relationship between mass and volume. It introduces direct variation, rational functions, and how these principles apply to ship design for optimal floating capacity. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 3 | Closed Captioned Video: Geometry Applications: Area and Volume, 3TopicArea and Volume DescriptionThis segment explores the surface area-to-volume ratio using the Citigroup Building as an example. It discusses how this ratio impacts energy efficiency in buildings and compares it to natural examples like polar bears and snakes for context. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 1 | Closed Captioned Video: Geometry Applications: Area and Volume, 1TopicArea and Volume DescriptionThis segment explores the concept of density, using the Titanic to demonstrate buoyancy and the relationship between mass and volume. It introduces direct variation, rational functions, and how these principles apply to ship design for optimal floating capacity. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume | Closed Captioned Video: Geometry Applications: Area and VolumeTopicArea and Volume |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 1 | Closed Captioned Video: Geometry Applications: Area and Volume, 1TopicArea and Volume DescriptionThis segment explores the concept of density, using the Titanic to demonstrate buoyancy and the relationship between mass and volume. It introduces direct variation, rational functions, and how these principles apply to ship design for optimal floating capacity. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 1 | Closed Captioned Video: Geometry Applications: Area and Volume, 1TopicArea and Volume DescriptionThis segment explores the concept of density, using the Titanic to demonstrate buoyancy and the relationship between mass and volume. It introduces direct variation, rational functions, and how these principles apply to ship design for optimal floating capacity. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 1 | Closed Captioned Video: Geometry Applications: Area and Volume, 1TopicArea and Volume DescriptionThis segment explores the concept of density, using the Titanic to demonstrate buoyancy and the relationship between mass and volume. It introduces direct variation, rational functions, and how these principles apply to ship design for optimal floating capacity. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 1 | Closed Captioned Video: Geometry Applications: Area and Volume, 1TopicArea and Volume DescriptionThis segment explores the concept of density, using the Titanic to demonstrate buoyancy and the relationship between mass and volume. It introduces direct variation, rational functions, and how these principles apply to ship design for optimal floating capacity. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 1 | Closed Captioned Video: Geometry Applications: Area and Volume, 1TopicArea and Volume DescriptionThis segment explores the concept of density, using the Titanic to demonstrate buoyancy and the relationship between mass and volume. It introduces direct variation, rational functions, and how these principles apply to ship design for optimal floating capacity. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 1 | Closed Captioned Video: Geometry Applications: Area and Volume, 1TopicArea and Volume DescriptionThis segment explores the concept of density, using the Titanic to demonstrate buoyancy and the relationship between mass and volume. It introduces direct variation, rational functions, and how these principles apply to ship design for optimal floating capacity. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 3 | Closed Captioned Video: Geometry Applications: Area and Volume, 3TopicArea and Volume DescriptionThis segment explores the surface area-to-volume ratio using the Citigroup Building as an example. It discusses how this ratio impacts energy efficiency in buildings and compares it to natural examples like polar bears and snakes for context. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 3 | Closed Captioned Video: Geometry Applications: Area and Volume, 3TopicArea and Volume DescriptionThis segment explores the surface area-to-volume ratio using the Citigroup Building as an example. It discusses how this ratio impacts energy efficiency in buildings and compares it to natural examples like polar bears and snakes for context. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 3 | Closed Captioned Video: Geometry Applications: Area and Volume, 3TopicArea and Volume DescriptionThis segment explores the surface area-to-volume ratio using the Citigroup Building as an example. It discusses how this ratio impacts energy efficiency in buildings and compares it to natural examples like polar bears and snakes for context. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume | Closed Captioned Video: Geometry Applications: Area and VolumeTopicArea and Volume |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume | Closed Captioned Video: Geometry Applications: Area and VolumeTopicArea and Volume |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume | Closed Captioned Video: Geometry Applications: Area and VolumeTopicArea and Volume |
Applications of Surface Area and Volume, Surface Area and Volume |