
Illustrative Math Alignment: Grade 6 Unit 1
Dividing Fractions
Lesson 15: Volume of Prisms
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Math Example--Volume Concepts--Calculating Volume: Example 3 | Math Example--Volume Concepts--Calculating Volume: Example 3TopicVolume DescriptionA hollow rectangular prism with outer dimensions: length = 60, width = 20, and height = 16. The inner hollow part has dimensions: length = 60, width = 18, and height = 14. The image shows how to subtract volumes to find the hollow volume. This image illustrates Example 3: The caption explains how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume. V = (60 * 20 * 16) - (60 * 18 * 14) = 4080. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 4 | Math Example--Volume Concepts--Calculating Volume: Example 4TopicVolume DescriptionA hollow rectangular prism with outer dimensions labeled as x, y, and z, and inner hollow dimensions labeled as x - 2 and y - 2. The image shows a symbolic calculation for finding the hollow volume using variables. This image illustrates Example 4: The caption describes how to calculate the volume of a hollow rectangular prism by subtracting the inner volume from the outer volume using variables: V = xyz - z(y - 2)(x - 2) = 2z(y + x - 2). |
Volume |
|
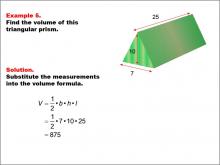
Math Example--Volume Concepts--Calculating Volume: Example 5 | Math Example--Volume Concepts--Calculating Volume: Example 5TopicVolume DescriptionThe image shows a triangular prism with dimensions labeled as base (7), height (10), and length (25). It is part of an example on how to calculate the volume of a solid triangular prism. This image illustrates Example 5: "Find the volume of this triangular prism." The solution involves substituting the given measurements into the volume formula for a triangular prism: V = 1/2 * b * h * l = 1/2 * 7 * 10 * 25 = 875. |
Volume |
|
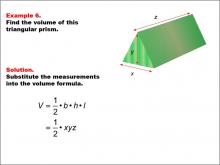
Math Example--Volume Concepts--Calculating Volume: Example 6 | Math Example--Volume Concepts--Calculating Volume: Example 6TopicVolume DescriptionThe image depicts a triangular prism with dimensions labeled as x, y, and z. The example demonstrates how to calculate the volume using a general formula for a triangular prism. This image illustrates Example 6: "Find the volume of this triangular prism." The solution uses the formula V = 1/2 * b * h * l, which is simplified to V = 1/2 * x * y * z.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 7 | Math Example--Volume Concepts--Calculating Volume: Example 7TopicVolume DescriptionThe image shows a hollow triangular prism with outer dimensions labeled as base (10), height (7), and length (35), and inner dimensions labeled as base (8) and height (5). The example calculates the volume by subtracting the hollow region from the full prism. This image illustrates Example 7: "Find the volume of this hollow triangular prism." The solution calculates the full volume using V = 1/2 * b1 * h1 * l1 - 1/2 * b2 * h2 * l2, which simplifies to V = 1/2 * 10 * 7 * 35 - 1/2 * 8 * 5 * 35 = 525.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 8 | Math Example--Volume Concepts--Calculating Volume: Example 8TopicVolume DescriptionThis image shows a hollow triangular prism with outer dimensions labeled as x, y, and z, and inner dimensions reduced by 2 units each. It demonstrates how to calculate the volume by subtracting the hollow region from the full prism. This image illustrates Example 8: "Find the volume of this hollow triangular prism." The solution uses V = 1/2 * b1 * h1 * l1 - 1/2 * b2 * h2 * l2, which simplifies to V = z(xy - (x - 2)(y - 2)) = z(x + y - 2).. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 9 | Math Example--Volume Concepts--Calculating Volume: Example 9TopicVolume Description
A green cylinder with a radius of 10 units and a height of 8 units. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 9: The task is to find the volume of the cylinder. The volume formula V = πr2h is used. Substituting the values r = 10 and h = 8, the volume is calculated as V= 800π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 10 | Math Example--Volume Concepts--Calculating Volume: Example 10TopicVolume DescriptionA green cylinder with a general radius y and height x. The radius is marked on the top surface, and the height is marked on the side. This image illustrates Example 10: The task is to find the volume of this cylinder. The volume formula V = πr2h is used, and substituting r = y and h = x, the volume is calculated as V = xy2π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 11 | Math Example--Volume Concepts--Calculating Volume: Example 11TopicVolume DescriptionA hollow green cylinder with an outer radius of 10 units, an inner radius of 9 units, and a height of 15 units. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 11: The task is to find the volume of this hollow cylinder. The volume formula for a hollow cylinder V = πr12h1 - πr22h2 is used. Substituting values, the result is V = 285π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 12 | Math Example--Volume Concepts--Calculating Volume: Example 12TopicVolume DescriptionA hollow green cylinder with an outer radius y, an inner radius y - 1, and a height x. The radii are marked on the top surface, and the height is marked on the side. This image illustrates Example 12: The task is to find the volume of this hollow cylinder. Using V = π(r12h1 - r22h2), substituting values gives: V = πx(y2 - (y - 1)2= πx(2y - 1). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 13 | Math Example--Volume Concepts--Calculating Volume: Example 13TopicVolume DescriptionA rectangular-based pyramid is shown with dimensions: base length 10, base width 8, and height 30. The image demonstrates how to calculate the volume of this pyramid. This image illustrates Example 13: The caption provides a step-by-step solution for calculating the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h. Substituting values: V = (1/3) * 8 * 10 * 30 = 800. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 14 | Math Example--Volume Concepts--Calculating Volume: Example 14TopicVolume DescriptionA general rectangular-based pyramid is shown with variables x, y, and z representing the base dimensions and height. This example shows how to calculate the volume of a pyramid using variables instead of specific numbers. This image illustrates Example 14: The caption explains how to calculate the volume of a pyramid with a rectangular base using the formula V = (1/3) * Area of Base * h, which simplifies to V = (1/3) * x * y * z. |
Volume |
|
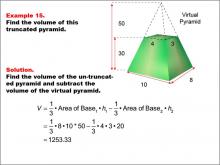
Math Example--Volume Concepts--Calculating Volume: Example 15 | Math Example--Volume Concepts--Calculating Volume: Example 15TopicVolume |
Volume |
|
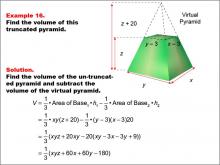
Math Example--Volume Concepts--Calculating Volume: Example 16 | Math Example--Volume Concepts--Calculating Volume: Example 16TopicVolume DescriptionA truncated rectangular-based pyramid is shown with variables x, y, and z representing dimensions. The smaller virtual pyramid has reduced dimensions by 3 units for both width and length and reduced height by z - 20. The image demonstrates how to calculate the volume in terms of variables. This image illustrates Example 16: The caption explains how to find the volume of a truncated pyramid using variables for both pyramids' dimensions. Formula: V = (1/3) * xy(z + 20) - (1/3) * (y - 3)(x - 3)(z), which simplifies to V = (1/3) * (xyz + 60x + 60y - 180). |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 17 | Math Example--Volume Concepts--Calculating Volume: Example 17TopicVolume DescriptionA green sphere with a radius labeled as 3. The image is part of a math example showing how to calculate the volume of a sphere. This image illustrates Example 17: The text describes finding the volume of a sphere. The formula used is V = (4/3) * π * r3, where r = 3. After substituting, the result is V = 36π. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 18 | Math Example--Volume Concepts--Calculating Volume: Example 18TopicVolume Description
A green sphere with a radius labeled as x. This image is part of a math example showing how to calculate the volume of a sphere using an unknown radius. This image illustrates Example 18: The text explains how to find the volume of a sphere with an unknown radius x. The formula used is V = (4/3) * π * r3, and substituting r = x gives V = (4/3) * x3 * π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 19 | Math Example--Volume Concepts--Calculating Volume: Example 19TopicVolume Description
A green cube with side length labeled as 7. The image illustrates how to calculate the volume of a cube with known side length. This image illustrates Example 19: The text describes finding the volume of a cube. The formula used is V = s3, where s = 7. After substituting, the result is V = 343. Volume is a fundamental concept in geometry that helps students understand the space occupied by three-dimensional objects. In this collection, each example uses various geometric shapes to calculate volume, showcasing real-life applications of volume in different shapes. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 20 | Math Example--Volume Concepts--Calculating Volume: Example 20TopicVolume DescriptionA green cube with side length labeled as x. This image is part of a math example showing how to calculate the volume of a cube using an unknown side length. This image illustrates Example 20: The text explains how to find the volume of a cube with an unknown side length x. The formula used is V = s3, and substituting s = x gives V = x3. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 21 | Math Example--Volume Concepts--Calculating Volume: Example 21TopicVolume DescriptionA hollow cube with an outer edge of 9 and an inner hollow region with an edge of 7. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 21: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 is the outer edge (9) and s2 is the inner edge (7). The solution calculates 9^3 - 7^3 = 386.. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 22 | Math Example--Volume Concepts--Calculating Volume: Example 22TopicVolume DescriptionA hollow cube with an outer edge of x and an inner hollow region with an edge of x - 2. The image shows how to calculate the volume by subtracting the volume of the inner cube from the outer cube. This image illustrates Example 22: Find the volume of a hollow cube. The formula used is V = s13 - s23, where s1 = x and s2 = x - 2. Expanding and simplifying gives V = 6x2 - 12x + 8. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 23 | Math Example--Volume Concepts--Calculating Volume: Example 23TopicVolume Description
A cone with a height of 12 and a radius of 4. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 23: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = 4 and h = 12. Substituting these values gives V = (1/3) * π * (42) * 12 = 64π. |
Volume |

|
Math Example--Volume Concepts--Calculating Volume: Example 24 | Math Example--Volume Concepts--Calculating Volume: Example 24TopicVolume DescriptionA cone with a height labeled as y and a radius labeled as x. The image shows how to calculate its volume using the cone volume formula (V = 1/3 * π * r2 * h). This image illustrates Example 24: Find the volume of a cone. The formula used is V = (1/3) * π * r2 * h, where r = x and h = y. Substituting these variables gives V = (x^2 * y)/3 * π. |
Volume |

|
Definition--3D Geometry Concepts--Volume | VolumeTopic3D Geometry DefinitionVolume is the measure of the amount of space occupied by a three-dimensional object, expressed in cubic units. DescriptionVolume is a fundamental concept in the study of three-dimensional geometry. It quantifies the capacity of a 3D object, indicating how much space it occupies. This measurement is crucial in various fields, including mathematics, engineering, architecture, and physical sciences. |
Volume |

|
Definition--3D Geometry Concepts--Volume | VolumeTopic3D Geometry DefinitionVolume is the measure of the amount of space occupied by a three-dimensional object, expressed in cubic units. DescriptionVolume is a fundamental concept in the study of three-dimensional geometry. It quantifies the capacity of a 3D object, indicating how much space it occupies. This measurement is crucial in various fields, including mathematics, engineering, architecture, and physical sciences. |
Volume |

|
Definition--3D Geometry Concepts--Volume | VolumeTopic3D Geometry DefinitionVolume is the measure of the amount of space occupied by a three-dimensional object, expressed in cubic units. DescriptionVolume is a fundamental concept in the study of three-dimensional geometry. It quantifies the capacity of a 3D object, indicating how much space it occupies. This measurement is crucial in various fields, including mathematics, engineering, architecture, and physical sciences. |
Volume |

|
Definition--3D Geometry Concepts--Volume | VolumeTopic3D Geometry DefinitionVolume is the measure of the amount of space occupied by a three-dimensional object, expressed in cubic units. DescriptionVolume is a fundamental concept in the study of three-dimensional geometry. It quantifies the capacity of a 3D object, indicating how much space it occupies. This measurement is crucial in various fields, including mathematics, engineering, architecture, and physical sciences. |
Volume |

|
Formulas--Volume of a Cube | Formulas--Volume of a Cube
The formula for the Volume of a Cube. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
Formulas--Volume of a Cube | Formulas--Volume of a Cube
The formula for the Volume of a Cube. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
Formulas--Volume of a Cube | Formulas--Volume of a Cube
The formula for the Volume of a Cube. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
Formulas--Volume of a Cylinder | Formulas--Volume of a Cylinder
The formula for the Volume of a Cylinder. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume and Cylinders |

|
Formulas--Volume of a Cylinder | Formulas--Volume of a Cylinder
The formula for the Volume of a Cylinder. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume and Cylinders |

|
Formulas--Volume of a Cylinder | Formulas--Volume of a Cylinder
The formula for the Volume of a Cylinder. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume and Cylinders |
|
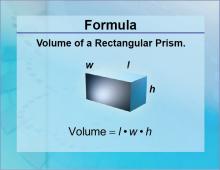
Formulas--Volume of a Rectangular Prism | Formulas--Volume of a Rectangular Prism
The formula for the Volume of a Recantular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
Formulas--Volume of a Rectangular Prism | Formulas--Volume of a Rectangular Prism
The formula for the Volume of a Recantular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
Formulas--Volume of a Rectangular Prism | Formulas--Volume of a Rectangular Prism
The formula for the Volume of a Recantular Prism. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
Formulas--Volume of a Sphere | Formulas--Volume of a Sphere
The formula for the Volume of a Sphere. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
Formulas--Volume of a Sphere | Formulas--Volume of a Sphere
The formula for the Volume of a Sphere. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
Formulas--Volume of a Sphere | Formulas--Volume of a Sphere
The formula for the Volume of a Sphere. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |
|
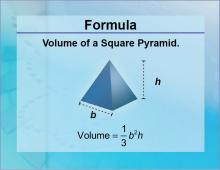
Formulas--Volume of a Square Pyramid | Formulas--Volume of a Square Pyramid
The formula for the Volume of a Square Pyramid. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
Formulas--Volume of a Square Pyramid | Formulas--Volume of a Square Pyramid
The formula for the Volume of a Square Pyramid. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |

|
Formulas--Volume of a Square Pyramid | Formulas--Volume of a Square Pyramid
The formula for the Volume of a Square Pyramid. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file.Related ResourcesTo see resources related to this topic click on the Related Resources tab above. |
Volume |
|
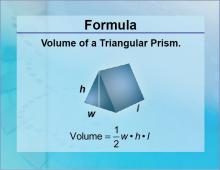
Formulas--Volume of a Triangular Prism | Note: The download is a JPG file. Related ResourcesTo see the complete collection of Formulas, click on this link: https://media4math.com/math-formulas |
Volume |

|
Formulas--Volume of a Triangular Prism | Note: The download is a JPG file. Related ResourcesTo see the complete collection of Formulas, click on this link: https://media4math.com/math-formulas |
Volume |

|
Formulas--Volume of a Triangular Prism | Note: The download is a JPG file. Related ResourcesTo see the complete collection of Formulas, click on this link: https://media4math.com/math-formulas |
Volume |
|
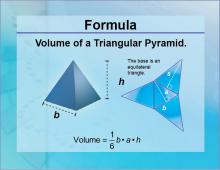
Formulas--Volume of a Triangular Pyramid | Volume of a Triangular Pyramid
Watch this video to learn about the volume of a pyramid. (The video transcript is also included.) Your browser does not support the video tag. Video Transcript Pyramids are majestic and a bit mysterious. Arising from deserts and jungles, they are grand in size and sleek in appearance. Mathematically, pyramids also have an air of mystery. Let’s take a closer look. Here is a cube of side s. Its volume couldn’t be more straightforward: s • s •s, or s-cubed. Its name, its shape, its volume are straightforward. |
Volume |

|
Formulas--Volume of a Triangular Pyramid | Volume of a Triangular Pyramid
Watch this video to learn about the volume of a pyramid. (The video transcript is also included.) Your browser does not support the video tag. Video Transcript Pyramids are majestic and a bit mysterious. Arising from deserts and jungles, they are grand in size and sleek in appearance. Mathematically, pyramids also have an air of mystery. Let’s take a closer look. Here is a cube of side s. Its volume couldn’t be more straightforward: s • s •s, or s-cubed. Its name, its shape, its volume are straightforward. |
Volume |

|
Formulas--Volume of a Triangular Pyramid | Volume of a Triangular Pyramid
Watch this video to learn about the volume of a pyramid. (The video transcript is also included.) Your browser does not support the video tag. Video Transcript Pyramids are majestic and a bit mysterious. Arising from deserts and jungles, they are grand in size and sleek in appearance. Mathematically, pyramids also have an air of mystery. Let’s take a closer look. Here is a cube of side s. Its volume couldn’t be more straightforward: s • s •s, or s-cubed. Its name, its shape, its volume are straightforward. |
Volume |

|
Promethean Flipchart: Geometry Applications: Area And Volume 3 | The Citibank Tower in New York City presents some unique design challenges. In addition it has to cope with a problem that all tall structure have to deal with: heat loss. By managing the ratio of surface area to volume, a skyscraper can effective manage heat loss. Note: The download for this resources is the Promethean Flipchart. To access the full video [Geometry Applications: Area and Volume, Segment 3: Ratio of Surface Area to Volume]: https://www.media4math.com/library/geometry-applications-area-and-volume-segment-3-ratio-surface-area-volume |
Applications of Surface Area and Volume |

|
Promethean Flipchart: Geometry Applications: Area And Volume 3 | The Citibank Tower in New York City presents some unique design challenges. In addition it has to cope with a problem that all tall structure have to deal with: heat loss. By managing the ratio of surface area to volume, a skyscraper can effective manage heat loss. Note: The download for this resources is the Promethean Flipchart. To access the full video [Geometry Applications: Area and Volume, Segment 3: Ratio of Surface Area to Volume]: https://www.media4math.com/library/geometry-applications-area-and-volume-segment-3-ratio-surface-area-volume |
Applications of Surface Area and Volume |

|
Promethean Flipchart: Geometry Applications: Area And Volume 3 | The Citibank Tower in New York City presents some unique design challenges. In addition it has to cope with a problem that all tall structure have to deal with: heat loss. By managing the ratio of surface area to volume, a skyscraper can effective manage heat loss. Note: The download for this resources is the Promethean Flipchart. To access the full video [Geometry Applications: Area and Volume, Segment 3: Ratio of Surface Area to Volume]: https://www.media4math.com/library/geometry-applications-area-and-volume-segment-3-ratio-surface-area-volume |
Applications of Surface Area and Volume |