
Illustrative Math Alignment: Grade 6 Unit 1
Dividing Fractions
Lesson 15: Volume of Prisms
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Closed Captioned Video: Geometry Applications: Area and Volume, 3 | Closed Captioned Video: Geometry Applications: Area and Volume, 3TopicArea and Volume DescriptionThis segment explores the surface area-to-volume ratio using the Citigroup Building as an example. It discusses how this ratio impacts energy efficiency in buildings and compares it to natural examples like polar bears and snakes for context. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Geometry Applications: Area and Volume, 2 | Closed Captioned Video: Geometry Applications: Area and Volume, 2TopicArea and Volume DescriptionThis segment focuses on surface area, using the Louvre Pyramid to highlight geometric tessellations and triangular net calculations. It explains the surface area formula for pyramids and how these calculations are applied in architectural design and material efficiency. |
Applications of Surface Area and Volume, Surface Area and Volume |

|
Closed Captioned Video: Algebra Applications: Rational Functions, 2 | Closed Captioned Video: Algebra Applications: Rational Functions, 2TopicRational Functions DescriptionExamines surface area to volume ratios in animals using rational functions, connecting these ratios to evolutionary adaptations in different climates. This video provides a detailed explanation of examines surface area to volume ratios in animals using rational functions, connecting these ratios to evolutionary adaptations in different climates and its significance in understanding rational functions. |
Rational Expressions and Rational Functions and Equations |

|
Closed Captioned Video: Algebra Applications: Rational Functions, 2 | Closed Captioned Video: Algebra Applications: Rational Functions, 2TopicRational Functions DescriptionExamines surface area to volume ratios in animals using rational functions, connecting these ratios to evolutionary adaptations in different climates. This video provides a detailed explanation of examines surface area to volume ratios in animals using rational functions, connecting these ratios to evolutionary adaptations in different climates and its significance in understanding rational functions. |
Rational Expressions and Rational Functions and Equations |

|
Closed Captioned Video: Algebra Applications: Rational Functions, 1 | Closed Captioned Video: Algebra Applications: Rational Functions, 1TopicRational Functions DescriptionExplains submarine pressure and volume relationships using rational functions, illustrating depth impacts on vessel integrity and scuba safety. This video provides a detailed explanation of explains submarine pressure and volume relationships using rational functions, illustrating depth impacts on vessel integrity and scuba safety. and its significance in understanding rational functions. |
Rational Expressions and Rational Functions and Equations |

|
Closed Captioned Video: Geometry Applications--Pyramid Volume | Closed Captioned Video: Geometry Applications--Pyramid Volume
In this video, students see a derivation of the formula for the volume of a pyramid. This involves a hands-on activity using unit cubes, along with analysis, and a detailed algebraic derivation. |
Pyramids |

|
Closed Captioned Video: Geometry Applications--Pyramid Volume | Closed Captioned Video: Geometry Applications--Pyramid Volume
In this video, students see a derivation of the formula for the volume of a pyramid. This involves a hands-on activity using unit cubes, along with analysis, and a detailed algebraic derivation. |
Pyramids |

|
Closed Captioned Video: Geometry Applications--Pyramid Volume | Closed Captioned Video: Geometry Applications--Pyramid Volume
In this video, students see a derivation of the formula for the volume of a pyramid. This involves a hands-on activity using unit cubes, along with analysis, and a detailed algebraic derivation. |
Pyramids |

|
Closed Captioned Video: Geometry Applications--Pyramid Volume | Closed Captioned Video: Geometry Applications--Pyramid Volume
In this video, students see a derivation of the formula for the volume of a pyramid. This involves a hands-on activity using unit cubes, along with analysis, and a detailed algebraic derivation. |
Pyramids |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 6 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 6TopicPolynomials DescriptionA cubic example where the volume of a cube, A = x3 + 3x2 + 3x + 1, is used to find the side length. Example 6: Given the volume A = x3 + 3x2 + 3x + 1, factor as (x + 1)3, so the side lengths are x + 1. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 7 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 7TopicPolynomials DescriptionAnother cubic example solving for side length with volume A = x3 - 3x2 + 3x - 1. Example 7: For the volume A = x3 - 3x2 + 3x - 1, express as (x - 1)3 to determine side lengths of x - 1. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 1 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 1TopicPolynomials DescriptionAn example showing how to find the side lengths of a square given its area, A = x2+ 2x + 1. Example 1: Given the area A = x2+ 2x + 1, find the side lengths. Solution: Express the area as a perfect square, (x + 1)2, so the side lengths are x + 1. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 2 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 2TopicPolynomials DescriptionAnother example of finding the side lengths of a square with area A = x2+ 4x + 4. Example 2: Given A = x2+ 4x + 4, find the side lengths. Solution: Factor as (x + 2)2, so the side lengths are x + 2. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 3 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 3TopicPolynomials DescriptionShows how to determine the side lengths of a square with area A = x2 - 2x + 1. Example 3: For A = x2 - 2x + 1, the solution expresses it as (x - 1)2, making the side lengths x - 1. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 4 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 4TopicPolynomials DescriptionExample solving for side lengths of a square with area A = x2 - 4x + 4. Example 4: Given A = x2 - 4x + 4, factor as (x - 2)2 to find side lengths x - 2. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 5 | Math Example--Polynomial Concepts-- Perfect Squares and Cubes--Example 5TopicPolynomials DescriptionSolves for side lengths of a square with area A = x2 + 6x + 9. Example 5: With A = x2 + 6x + 9, factor as (x + 3)2, giving side lengths x + 3. Polynomials involve expressions with variables raised to powers, and these examples specifically address perfect squares and cubes. Each example in this collection explores how to derive side lengths or volumes using factorization, demonstrating the practical applications of polynomial expressions. |
Variable Expressions |

|
Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 1 | Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 1
This is part of a collection of math examples that focus on volume. |
Volume |

|
Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 2 | Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 2
This is part of a collection of math examples that focus on volume. |
Volume |
|
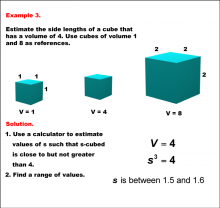
Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 3 | Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 3
This is part of a collection of math examples that focus on volume. |
Volume |

|
Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 4 | Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 4
This is part of a collection of math examples that focus on volume. |
Volume |

|
Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 5 | Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 5
This is part of a collection of math examples that focus on volume. |
Volume |

|
Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 6 | Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 6
This is part of a collection of math examples that focus on volume. |
Volume |

|
Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 7 | Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 7
This is part of a collection of math examples that focus on volume. |
Volume |

|
Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 8 | Math Example--Volume Concepts--Exploring Volumes of Cubes: Example 8
This is part of a collection of math examples that focus on volume. |
Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 1 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 1
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 1 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 1
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 2 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 2
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 2 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 2
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 3 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 3
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 3 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 3
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 4 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 4
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 4 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 4
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 5 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 5
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 5 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 5
This is part of a collection of math examples that focus on volume. |
Mass and Volume |
|
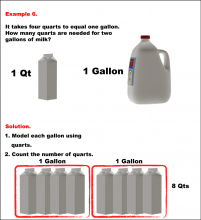
Math Example--Volume Concepts--Calculating Mass and Volume--Example 6 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 6
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 6 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 6
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 7 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 7
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 7 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 7
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 8 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 8
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 8 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 8
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 9 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 9
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 9 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 9
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 10 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 10
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Math Example--Volume Concepts--Calculating Mass and Volume--Example 10 | Math Example--Volume Concepts--Calculating Mass and Volume--Example 10
This is part of a collection of math examples that focus on volume. |
Mass and Volume |

|
Video Transcript: Geometry Applications--Volume of a Pyramid | Video Transcript: Geometry Applications--Volume of a Pyramid
This is the transcript for video entitled: "Geometry Applications--Volume of a Pyramid." This is part of a collection of video transcript from the Geometry Applications video series. To see the complete collection of transcripts, click on this link. Note: The download is a PDF file. Video Transcript LibraryTo see the complete collection of video transcriptsy, click on this link. Video LibraryTo see the complete collection of videos in the Video Library, click on this link. |
Pyramids |