
Illustrative Math Alignment: Grade 6 Unit 1
Dividing Fractions
Lesson 17: Fitting Boxes into Boxes
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Nodes |
|---|---|---|---|

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 7)--Lesson 2--Unit Rates and Complex Fractions | Lesson Plan: Unit Rates and Complex Fractions This lesson introduces seventh-grade students to unit rates and complex fractions, helping them develop a deeper understanding of proportional relationships and fraction operations. Students will learn to compute unit rates with fractional quantities, simplify complex fractions, and apply these skills to real-world situations such as speed calculations, recipe adjustments, and measurement conversions. |
Ratios and Rates and Applications of Ratios, Proportions, and Percents |

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 7)--Lesson 2--Unit Rates and Complex Fractions | Lesson Plan: Unit Rates and Complex Fractions This lesson introduces seventh-grade students to unit rates and complex fractions, helping them develop a deeper understanding of proportional relationships and fraction operations. Students will learn to compute unit rates with fractional quantities, simplify complex fractions, and apply these skills to real-world situations such as speed calculations, recipe adjustments, and measurement conversions. |
Ratios and Rates and Applications of Ratios, Proportions, and Percents |

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 7)--Lesson 2--Unit Rates and Complex Fractions | Lesson Plan: Unit Rates and Complex Fractions This lesson introduces seventh-grade students to unit rates and complex fractions, helping them develop a deeper understanding of proportional relationships and fraction operations. Students will learn to compute unit rates with fractional quantities, simplify complex fractions, and apply these skills to real-world situations such as speed calculations, recipe adjustments, and measurement conversions. |
Ratios and Rates and Applications of Ratios, Proportions, and Percents |

|
Lesson Plan--Ratios, Proportions, and Percents (Gr 7)--Lesson 2--Unit Rates and Complex Fractions | Lesson Plan: Unit Rates and Complex Fractions This lesson introduces seventh-grade students to unit rates and complex fractions, helping them develop a deeper understanding of proportional relationships and fraction operations. Students will learn to compute unit rates with fractional quantities, simplify complex fractions, and apply these skills to real-world situations such as speed calculations, recipe adjustments, and measurement conversions. |
Ratios and Rates and Applications of Ratios, Proportions, and Percents |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 10--Subtracting Mixed Numbers | Lesson Plan: Subtracting Mixed Numbers In this final lesson of the Adding and Subtracting Fractions Unit, students will learn how to subtract mixed numbers. This lesson builds on their understanding of mixed numbers and fraction subtraction, helping them develop strategies for subtracting whole numbers and fractions together. Students will: |
Add and Subtract Mixed Numbers |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 9--Adding Mixed Numbers | Lesson Plan: Adding Mixed Numbers In this ninth lesson of the Adding and Subtracting Fractions Unit, students will learn how to add mixed numbers. This lesson builds on their understanding of mixed numbers and fraction addition, providing strategies for combining whole numbers and fractions efficiently. Students will: |
Add and Subtract Mixed Numbers |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 8--Review of Mixed Numbers | Lesson Plan: Review of Mixed Numbers In this eighth lesson of the Adding and Subtracting Fractions Unit, students will review the concept of mixed numbers. This lesson reinforces students’ understanding of mixed numbers, improper fractions, and how to convert between the two, laying the groundwork for adding and subtracting mixed numbers in future lessons. Students will: |
Fractions and Mixed Numbers |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 7--Subtracting Fractions with Unlike Denominators | Lesson Plan: Subtracting Fractions with Unlike Denominators In this seventh lesson of the Adding and Subtracting Fractions Unit, students will learn how to subtract fractions with unlike denominators. This essential skill builds on their understanding of finding common denominators and equivalent fractions, enabling them to successfully subtract fractions with different denominators. Students will: |
Add and Subtract Fractions |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 6--Adding Fractions with Unlike Denominators | Lesson Plan: Adding Fractions with Unlike Denominators In this sixth lesson of the Adding and Subtracting Fractions Unit, students will learn how to add fractions with unlike denominators. This skill builds on their understanding of finding common denominators and equivalent fractions, allowing them to successfully combine fractions with different denominators. Students will: |
Add and Subtract Fractions |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 5--Finding Common Denominators | Lesson Plan: Finding Common Denominators In this fifth lesson of the Adding and Subtracting Fractions Unit, students will learn how to find common denominators, a critical skill for adding and subtracting fractions with unlike denominators. By understanding how to determine the Least Common Denominator (LCD), students will be better prepared to rewrite fractions as equivalent fractions with a shared denominator. Students will: |
Least Common Denominator |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 4--Subtracting Fractions with Like Denominators | Lesson Plan: Subtracting Fractions with Like Denominators In this fourth lesson of the Adding and Subtracting Fractions Unit, students will learn how to subtract fractions with like denominators. Since the denominators are the same, students can focus on subtracting numerators and reinforcing their understanding of fraction subtraction. Students will: |
Add and Subtract Fractions |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 3--Adding Fractions with Like Denominators | Lesson Plan: Adding Fractions with Like Denominators In this third lesson of the Adding and Subtracting Fractions Unit, students will learn how to add fractions with like denominators. Since the denominators are the same, students can focus on adding numerators and reinforcing their understanding of fraction addition. Students will: |
Add and Subtract Fractions |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 2--Review of LCM and GCF | Lesson Plan: Review LCM and GCF This second lesson in the Adding and Subtracting Fractions Unit focuses on the essential concepts of Least Common Multiple (LCM) and Greatest Common Factor (GCF). Understanding these concepts is critical for working with fractions, especially when finding common denominators for addition and subtraction. Students will: |
Find Greatest Common Factors |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 2--Review of LCM and GCF | Lesson Plan: Review LCM and GCF This second lesson in the Adding and Subtracting Fractions Unit focuses on the essential concepts of Least Common Multiple (LCM) and Greatest Common Factor (GCF). Understanding these concepts is critical for working with fractions, especially when finding common denominators for addition and subtraction. Students will: |
Find Greatest Common Factors |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 2--Review of LCM and GCF | Lesson Plan: Review LCM and GCF This second lesson in the Adding and Subtracting Fractions Unit focuses on the essential concepts of Least Common Multiple (LCM) and Greatest Common Factor (GCF). Understanding these concepts is critical for working with fractions, especially when finding common denominators for addition and subtraction. Students will: |
Find Greatest Common Factors |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 1--Understanding Equivalent Fractions | Lesson Plan: Understanding Equivalent Fractions This first lesson in the Adding and Subtracting Fractions Unit introduces students to the fundamental concepts of fraction addition and subtraction. By using visual models and real-world examples, students will develop an understanding of what it means to combine and take away fractional parts. Students will: |
Find Equivalent Fractions |

|
Lesson Plan--Adding and Subtracting Fractions--Lesson 1--Understanding Equivalent Fractions | Lesson Plan: Understanding Equivalent Fractions This first lesson in the Adding and Subtracting Fractions Unit introduces students to the fundamental concepts of fraction addition and subtraction. By using visual models and real-world examples, students will develop an understanding of what it means to combine and take away fractional parts. Students will: |
Find Equivalent Fractions |

|
Lesson Plan--Fraction Basics--Lesson 4--Comparing Fractions | Lesson Plan: Comparing Fractions This comprehensive lesson teaches students how to compare fractions using multiple strategies. By leveraging visual models, number lines, and mathematical reasoning, students will develop a strong foundation in fraction comparison. This lesson helps students understand when fractions are greater than, less than, or equal to one another, reinforcing key mathematical concepts. Students will: |
Compare and Order Fractions |

|
Lesson Plan--Fraction Basics--Lesson 3--Equivalent Fractions | Lesson Plan: Equivalent Fractions This engaging lesson introduces students to equivalent fractions, a key concept in developing strong fraction skills. Through interactive activities and visual models, students will learn how different fractions can represent the same value. By using fraction bars, number lines, and real-world examples, this lesson helps students grasp the idea of fraction equivalence in an intuitive way. Students will: |
Fractions and Mixed Numbers |

|
Lesson Plan--Fraction Basics--Lesson 2--Fractions on a Number Line | Lesson 2--Fractions on a Number Line This lesson plan, the second in a five-part series on fraction basics, introduces elementary students to the powerful concept of using number lines to understand fractions. Building on foundational knowledge from the first lesson, it leverages Media4Math.com's engaging resources to visualize fractions in a linear context. The lesson likely begins with a warm-up activity, reviewing previous fraction concepts before transitioning to the main focus: number lines. Students learn how to represent fractions on a number line, a crucial skill that helps them visualize fractions as precise points between whole numbers. |
Fractions and Mixed Numbers |

|
Lesson Plan--Fraction Basics--Lesson 1--What Is a Fraction? | Lesson 1--What Is a Fraction? This comprehensive lesson plan introduces elementary students to the fundamental concept of fractions. Designed as the first of five lessons in a unit on fractions, it utilizes engaging resources from Media4Math.com to make learning both interactive and effective. The lesson begins with a warm-up activity using pizza slices to illustrate the concept of fair sharing, setting the stage for understanding fractions as equal parts of a whole. Students then explore fraction basics through interactive slideshows, learning key terms like numerator and denominator. The plan incorporates various visual models, including circles and rectangles, to reinforce fraction concepts. Students practice identifying and labeling fractions, with a focus on developing a solid understanding of unit fractions. |
Fractions and Mixed Numbers |

|
Lesson Plan--Fraction Basics--Lesson 1--What Is a Fraction? | Lesson 1--What Is a Fraction? This comprehensive lesson plan introduces elementary students to the fundamental concept of fractions. Designed as the first of five lessons in a unit on fractions, it utilizes engaging resources from Media4Math.com to make learning both interactive and effective. The lesson begins with a warm-up activity using pizza slices to illustrate the concept of fair sharing, setting the stage for understanding fractions as equal parts of a whole. Students then explore fraction basics through interactive slideshows, learning key terms like numerator and denominator. The plan incorporates various visual models, including circles and rectangles, to reinforce fraction concepts. Students practice identifying and labeling fractions, with a focus on developing a solid understanding of unit fractions. |
Fractions and Mixed Numbers |

|
Math Clip Art Booklet: Fraction Number Lines | Number Lines for Fractions: Plotting and ComparingTeach Fractions Visually with Number LinesHelp your students master fractions with Number Lines for Fractions: Plotting and Comparing, a comprehensive resource for teaching fractions using number lines. This guide is designed for elementary teachers and offers a hands-on approach to teaching fractions, helping students develop a deep understanding of this essential math concept. With ready-to-use templates, students will learn how to plot fractions, compare values, and explore fraction equivalencies. The visual nature of number lines allows learners to see fractions as points on a continuum, making it easier to understand their relationships and operations. From comparing fractions with different denominators to visualizing addition and subtraction, this resource aligns with Common Core Standards for Grades 3–5. |
Find Equivalent Fractions |

|
Math Clip Art Booklet: Fraction Number Lines | Number Lines for Fractions: Plotting and ComparingTeach Fractions Visually with Number LinesHelp your students master fractions with Number Lines for Fractions: Plotting and Comparing, a comprehensive resource for teaching fractions using number lines. This guide is designed for elementary teachers and offers a hands-on approach to teaching fractions, helping students develop a deep understanding of this essential math concept. With ready-to-use templates, students will learn how to plot fractions, compare values, and explore fraction equivalencies. The visual nature of number lines allows learners to see fractions as points on a continuum, making it easier to understand their relationships and operations. From comparing fractions with different denominators to visualizing addition and subtraction, this resource aligns with Common Core Standards for Grades 3–5. |
Find Equivalent Fractions |

|
Math Clip Art Booklet: Fraction Number Lines | Number Lines for Fractions: Plotting and ComparingTeach Fractions Visually with Number LinesHelp your students master fractions with Number Lines for Fractions: Plotting and Comparing, a comprehensive resource for teaching fractions using number lines. This guide is designed for elementary teachers and offers a hands-on approach to teaching fractions, helping students develop a deep understanding of this essential math concept. With ready-to-use templates, students will learn how to plot fractions, compare values, and explore fraction equivalencies. The visual nature of number lines allows learners to see fractions as points on a continuum, making it easier to understand their relationships and operations. From comparing fractions with different denominators to visualizing addition and subtraction, this resource aligns with Common Core Standards for Grades 3–5. |
Find Equivalent Fractions |

|
Math Clip Art Booklet: Pizza Fractions | Discover the Power of Pizza Fractions: A Hands-On Guide for Elementary Math Teachers Engage your students with this exciting, hands-on resource for teaching fractions using pizza models. Fraction Fun with Pizza: Hands-On Activities for Elementary Math Teachers is a comprehensive guide designed to make learning fractions enjoyable and interactive. Perfect for educators teaching Grades 3-5, this 20-page booklet includes step-by-step instructions, activities, and printable Media4Math clip art to help students master foundational fraction concepts. |
Find Equivalent Fractions |

|
Math Clip Art Booklet: Fraction Bar Templates | Fraction Bars Toolkit: Visual Strategies for Fraction MasteryLooking for an engaging way to teach fractions in your elementary classroom? Our Fraction Bars Booklet is the ultimate resource to make fraction learning fun, visual, and interactive. Designed specifically for elementary math teachers, this booklet features customizable templates for fraction bars ranging from halves to twelfths. Students can cut, shade, and manipulate these fraction bars to explore fraction concepts, equivalencies, and operations like addition and subtraction. This hands-on approach helps bridge the gap between abstract fraction concepts and real-world understanding, fostering deeper numerical reasoning. |
Find Equivalent Fractions |

|
Math Clip Art Booklet: Fraction Bar Templates | Fraction Bars Toolkit: Visual Strategies for Fraction MasteryLooking for an engaging way to teach fractions in your elementary classroom? Our Fraction Bars Booklet is the ultimate resource to make fraction learning fun, visual, and interactive. Designed specifically for elementary math teachers, this booklet features customizable templates for fraction bars ranging from halves to twelfths. Students can cut, shade, and manipulate these fraction bars to explore fraction concepts, equivalencies, and operations like addition and subtraction. This hands-on approach helps bridge the gap between abstract fraction concepts and real-world understanding, fostering deeper numerical reasoning. |
Find Equivalent Fractions |
|
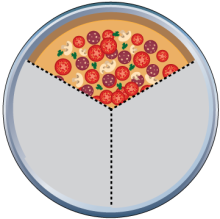
Math Clip Art--Equivalent Fractions Pizza Slices--One Third | Math Clip Art--Equivalent Fractions Pizza Slices--One ThirdTopicFractions DescriptionThis math clip art image depicts a pizza with one-third of it left to eat. The visual representation clearly illustrates the concept of fractions, showing how one part out of three equal parts forms the fraction one-third. As part of a collection of similar images showing various fractions, this visual aid can be used to introduce and reinforce the concept of fractions. Teachers can use this image alongside others to demonstrate different fractions, compare fractions, and introduce equivalent fractions. |
Find Equivalent Fractions |
|
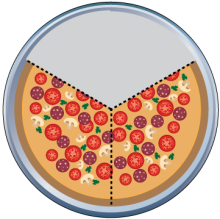
Math Clip Art--Equivalent Fractions Pizza Slices--Two Thirds | Math Clip Art--Equivalent Fractions Pizza Slices--Two ThirdsTopicFractions DescriptionThis math clip art showcases a pizza with two-thirds of it left to eat, offering a clear visual representation of the fraction 2/3. The image effectively demonstrates how two parts out of three equal parts constitute two-thirds, making it an invaluable tool for teaching fractions. When used in conjunction with other images in the collection, this visual aid can help students understand various fractions, compare different fractions, and explore the concept of equivalent fractions. Teachers can use this image to illustrate how two-thirds relates to one-third and to the whole. |
Find Equivalent Fractions |
|
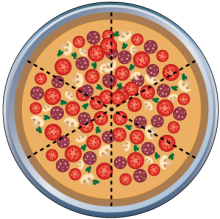
Math Clip Art--Equivalent Fractions Pizza Slices--Full Sixths | Math Clip Art--Equivalent Fractions Pizza Slices--Full SixthsTopicFractions DescriptionThis math clip art image presents a complete pizza sliced into six equal parts. It provides a visual representation of a whole divided into sixths, serving as a reference point for understanding fractions with a denominator of 6. As part of a comprehensive series of images illustrating various fractions and their representations, this visual aid can be used to enhance understanding of fractional concepts, especially the idea of a whole and its parts. Teachers can use this image as a starting point to demonstrate how different fractions are formed from these six equal parts. |
Find Equivalent Fractions |
|
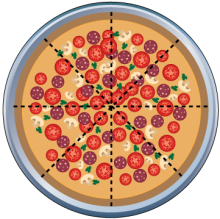
Math Clip Art--Equivalent Fractions Pizza Slices--Full Eighths | Math Clip Art--Equivalent Fractions Pizza Slices--Full EighthsTopicFractions DescriptionThis math clip art image presents a complete pizza sliced into eight equal parts. It provides a visual representation of a whole divided into eighths, serving as a reference point for understanding fractions with a denominator of 8. As part of a comprehensive series of images illustrating various fractions and their representations, this visual aid can be used to enhance understanding of fractional concepts, especially the idea of a whole and its parts. Teachers can use this image as a starting point to demonstrate how different fractions are formed from these eight equal parts. |
Find Equivalent Fractions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio) | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio)
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio) | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio)
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio) | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio)
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio) | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio)
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio) | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio)
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio) | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio)
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio) | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression (Spanish Audio)
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression | Video Definition 23--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression
TopicRationals and Radicals |
Rational Expressions |

|
Video Definition 23--Fraction Concepts--Mixed Number | Video Definition 23--Fraction Concepts--Mixed Number
TopicFractions DescriptionThe term Mixed Number describes a number that consists of a whole number and a proper fraction. Examples include 1 1/2, 2 3/4, and 12 2/3. The image explains that the mixed number format combines a whole number with a fractional part. Mixed numbers are a common representation in fractions, linking whole numbers and fractions together in real-world applications. |
Fractions and Mixed Numbers |
|
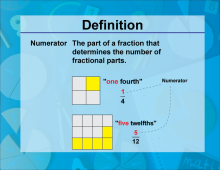
Video Definition 24--Fraction Concepts--Numerator | Video Definition 24--Fraction Concepts--Numerator
TopicFractions DescriptionThe term Numerator represents the part of a fraction that indicates how many parts of the whole are being considered. For example, in 1/4, the numerator is 1, meaning one part out of four. The image uses visual models to illustrate numerators in fractions like 1/4 and 5/12. Understanding the numerator is critical for interpreting the value of a fraction and applying it to real-world problems. |
Fractions and Mixed Numbers |

|
Video Definition 24--Fraction Concepts--Numerator | Video Definition 24--Fraction Concepts--Numerator
TopicFractions DescriptionThe term Numerator represents the part of a fraction that indicates how many parts of the whole are being considered. For example, in 1/4, the numerator is 1, meaning one part out of four. The image uses visual models to illustrate numerators in fractions like 1/4 and 5/12. Understanding the numerator is critical for interpreting the value of a fraction and applying it to real-world problems. |
Fractions and Mixed Numbers |

|
Video Definition 23--Fraction Concepts--Mixed Number | Video Definition 23--Fraction Concepts--Mixed Number
TopicFractions DescriptionThe term Mixed Number describes a number that consists of a whole number and a proper fraction. Examples include 1 1/2, 2 3/4, and 12 2/3. The image explains that the mixed number format combines a whole number with a fractional part. Mixed numbers are a common representation in fractions, linking whole numbers and fractions together in real-world applications. |
Fractions and Mixed Numbers |