Illustrative Math Alignment: Grade 6 Unit 7

Rational Numbers

Lesson 16: Common Factors

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Nodes
Closed Captioned Video: Quadratics: Solving Quadratic Equations in Standard Form By Factoring	Closed Captioned Video: Quadratics: Solving Quadratic Equations in Standard Form By Factoring Topic Quadratics Description Factoring is explained as a method to solve quadratics expressed as products of binomials. Terms like factor pairs and standard form are covered. Applications include determining dimensions of rectangles, triangles, and squares.	Graphs of Quadratic Functions and Quadratic Equations and Functions
Closed Captioned Video: Quadratics: Solving Quadratic Equations in Standard Form By Factoring	Closed Captioned Video: Quadratics: Solving Quadratic Equations in Standard Form By Factoring Topic Quadratics Description Factoring is explained as a method to solve quadratics expressed as products of binomials. Terms like factor pairs and standard form are covered. Applications include determining dimensions of rectangles, triangles, and squares.	Graphs of Quadratic Functions and Quadratic Equations and Functions
Definition--Common Factor	Definition--Common Factor This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions and Variable Expressions
Definition--Common Factor	Definition--Common Factor This is part of a collection of math definitions from Media4Math's Visual Glossary.	Numerical Expressions and Variable Expressions
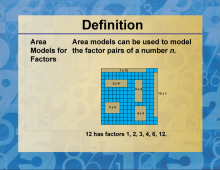
Definition--Factors and Multiples--Area Models for Factors	Area Models for Factors Topic Factors and Multiples Definition Factors are numbers that divide another number without leaving a remainder, while multiples are the result of multiplying a number by an integer. Description Understanding factors and multiples is crucial in mathematics, particularly in number theory and algebra. Factors are the building blocks of numbers, representing the integers that can be multiplied together to produce another number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. Multiples, on the other hand, are the product of a number and any integer. For instance, the multiples of 5 include 5, 10, 15, 20, and so on.	Numerical Expressions
Definition--Factors and Multiples--Common Factors	Common Factors Topic Factors and Multiples Definition A common factor is a number that divides two or more numbers exactly without leaving a remainder. Description Common factors are integral to understanding the mathematical concepts of factors and multiples. They are the numbers that can divide two or more given numbers without leaving a remainder. For example, if you consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. This is because these numbers can divide both 12 and 18 exactly, with no remainder.	Numerical Expressions
Definition--Factors and Multiples--Common Multiples	Common Multiples Topic Factors and Multiples Definition A common multiple is a number that is a multiple of two or more numbers. Description In the context of factors and multiples, understanding common multiples is crucial for solving various mathematical problems, particularly those involving fractions, least common multiples (LCM), and algebraic expressions. A common multiple of a set of numbers is a number that each of the numbers in the set divides without leaving a remainder. For example, the common multiples of 4 and 6 include 12, 24, 36, and so on. The smallest of these, 12, is known as the least common multiple (LCM).	Numerical Expressions
Definition--Factors and Multiples--Divisor	Divisor Topic Factors and Multiples Definition A divisor is a number that divides another number evenly, leaving no remainder. Description In the context of factors and multiples, a divisor plays a crucial role in understanding the relationships between numbers. A divisor is essentially a factor of a given number, as it divides that number without leaving a remainder. This concept is fundamental to identifying factors and understanding divisibility rules.	Numerical Expressions
Definition--Factors and Multiples--Factor Pairs	Factor Pairs Topic Factors and Multiples Definition Factor pairs are sets of two numbers that, when multiplied together, produce a given number. Description Factor pairs play a crucial role in understanding the relationships between numbers and their factors. They are essential in various mathematical operations, particularly in algebra and number theory. Factor pairs help students visualize the multiplicative structure of numbers and provide a foundation for more advanced concepts such as prime factorization and divisibility rules.	Numerical Expressions
Definition--Factors and Multiples--Factor Tree	Factor Tree Topic Factors and Multiples Definition A factor tree is a graphical method used to break down a number into its prime factors. Description A factor tree is a visual representation that helps in identifying the prime factors of a given number. It starts with the original number at the top and branches downwards, breaking the number into its factors until all the branches end in prime numbers. This method is particularly useful in understanding the concept of prime factorization, which is the process of expressing a number as the product of its prime factors.	Numerical Expressions
Definition--Factors and Multiples--Factoring Algebraic Expressions	Factoring Algebraic Expressions Topic Factors and Multiples Definition Factoring algebraic expressions involves breaking down a polynomial into simpler components called factors that, when multiplied together, give the original polynomial. Description Factoring algebraic expressions is a fundamental concept in algebra that plays a crucial role in simplifying expressions, solving equations, and understanding polynomial functions. This process involves expressing a polynomial as a product of its factors, which are simpler polynomials or numbers. For instance, the polynomial x^2 - 5x + 6 can be factored into (x - 2)(x - 3).	Numerical Expressions
Definition--Factors and Multiples--Factors	Factors Topic Factors and Multiples Definition Factors are numbers that divide evenly into another number without leaving a remainder. Description Factors play a crucial role in understanding the fundamental properties of numbers and their relationships. In the context of factors and multiples, factors are the building blocks that, when multiplied together, create a given number. This concept is essential for various mathematical operations and problem-solving techniques.	Numerical Expressions
Definition--Factors and Multiples--Greatest Common Factor (GCF)	Greatest Common Factor (GCF) Topic Factors and Multiples Definition The Greatest Common Factor (GCF) is the largest number that divides two or more numbers without leaving a remainder. Description The concept of the Greatest Common Factor (GCF) is crucial in the study of factors and multiples. The GCF is used to simplify fractions, find common denominators, and solve problems involving ratios. Understanding the GCF helps in breaking down complex problems into simpler parts, making it easier to handle large numbers and perform arithmetic operations efficiently.	Numerical Expressions
Definition--Factors and Multiples--LCM	Least Common Multiple (LCM) Topic Factors and Multiples Definition The least common multiple (LCM) is the smallest number that is a multiple of two or more numbers. Description The concept of the least common multiple (LCM) is essential in the study of factors and multiples. The LCM of two or more numbers is the smallest number that is evenly divisible by all of the given numbers. This concept is particularly useful in various mathematical operations and problem-solving scenarios.	Numerical Expressions
Definition--Factors and Multiples--Multiple	Multiples Topic Factors and Multiples Definition A multiple is a number that can be divided by another number without leaving a remainder. Description Multiples are fundamental in understanding the relationships between numbers in mathematics. They are particularly relevant when learning about factors and multiples, which are key concepts in elementary and middle school math curricula. A multiple of a number is obtained by multiplying that number by an integer. For example, the multiples of 5 include 5, 10, 15, 20, and so on.	Numerical Expressions
Definition--Factors and Multiples--Multiples of 10	Multiples of 10 Topic Factors and Multiples Definition Multiples of 10 are the numbers that result from multiplying 10 by any whole number. Description Multiples of 10 play a significant role in understanding factors and multiples. These numbers are easily recognizable as they always end in zero and form a predictable pattern on the number line. In the context of factors and multiples, multiples of 10 serve as an excellent example to illustrate the concept of multiples in general.	Numerical Expressions
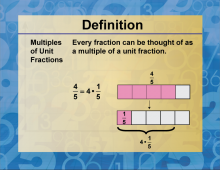
Definition--Factors and Multiples--Multiples of Unit Fractions	Multiples of Unit Fractions Topic Factors and Multiples Definition Multiples are the results obtained when a number is multiplied by an integer. Description In mathematics, understanding the concept of multiples is crucial, especially when dealing with factors and multiples. A multiple of a number is the product obtained when that number is multiplied by an integer. For example, the multiples of 3 include 3, 6, 9, 12, and so on. This concept is fundamental in various mathematical operations and problem-solving scenarios.	Numerical Expressions
Definition--Factors and Multiples--Prime Factorization	Prime Factorization Topic Factors and Multiples Definition Prime factorization is the process of breaking down a composite number into its prime factors. Description Prime factorization is a fundamental concept in the study of factors and multiples. It involves expressing a composite number as a product of prime numbers. For example, the number 60 can be factorized into 2 × 2 × 3 × 5. This process is crucial because it provides a unique representation of numbers, which is essential in various mathematical applications, including simplifying fractions, finding least common multiples (LCM), and greatest common divisors (GCD).	Numerical Expressions
Definition--Factors and Multiples--Prime Factors	Prime Factors Topic Factors and Multiples Definition Prime factors are the prime numbers that multiply together to give the original number. Description Prime factors are a fundamental concept in the study of factors and multiples. They are the building blocks of all numbers, as any integer greater than 1 can be expressed as a product of prime numbers. This process is known as prime factorization. For example, the prime factorization of 28 is 2 × 2 × 7, where 2 and 7 are prime numbers.	Numerical Expressions
Definition--Factors and Multiples--Proper Factors	Proper Factors Topic Factors and Multiples Definition Proper factors are the factors of a number excluding the number itself and 1. Description Proper factors play a significant role in the study of factors and multiples. Understanding proper factors is essential for grasping more complex mathematical concepts such as prime factorization, greatest common divisors, and least common multiples.	Numerical Expressions
Definition--Factors and Multiples--Simplifying Fractions Using Factoring	Simplifying Fractions with Factoring Topic Factors and Multiples Definition Simplifying fractions involves reducing the fraction to its simplest form by dividing both the numerator and the denominator by their greatest common factor (GCF).	Numerical Expressions
Definition--Factors and Multiples--Unknown Factors	Unknown Factors Topic Factors and Multiples Definition An unknown factor is a value in a multiplication equation that needs to be determined to solve the equation. Description Factors and multiples are fundamental concepts in mathematics, particularly in number theory and arithmetic. Understanding these concepts is crucial for solving a wide range of mathematical problems, from basic arithmetic to more advanced topics such as algebra and number theory. Factors of a number are the integers that can be multiplied together to produce that number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. These numbers can be paired in various ways to produce the product 12 (e.g., 2 x 6, 3 x 4).	Numerical Expressions
Definition--Factors and Multiples--Using the LCM to Find a Common Denominator	Using LCM to Find LCD Topic Factors and Multiples Definition The Least Common Multiple (LCM) of two or more numbers is used to find the Least Common Denominator (LCD) when working with fractions.	Numerical Expressions
Definition--Factors and Multiples--Visual Models of Multiples	Visual Models of Common Multiples Topic Factors and Multiples Definition Visual models of multiples are graphical representations that help illustrate the concept of multiples and common multiples of numbers, making it easier to understand their relationships and properties.	Numerical Expressions
Definition--Fraction Concepts--Greatest Common Factor (GCF)	Greatest Common Factor (GCF) Topic Fractions Definition The Greatest Common Factor (GCF) is the highest number that divides exactly into two or more numbers without leaving a remainder. Description The concept of the Greatest Common Factor (GCF) is crucial in the study of fractions. It is used to simplify fractions to their lowest terms, making them easier to work with and understand. When two or more fractions have the same GCF, it means they share a common factor that can be used to reduce each fraction to its simplest form. This process is essential for performing operations such as addition, subtraction, multiplication, and division of fractions.	Fractions and Mixed Numbers
Definition--Polynomial Concepts--Binomial Factor	Binomial Factor Topic Polynomials Definition A binomial factor is a two-term expression that, when multiplied by another factor, produces a given polynomial. Description Binomial factors are essential components in the study of polynomials, particularly in the context of factoring and solving polynomial equations. These two-term expressions play a crucial role in breaking down more complex polynomials into simpler, more manageable parts. Understanding binomial factors is key to mastering various algebraic techniques and problem-solving strategies.	Factoring Polynomials
Definition--Polynomial Concepts--Factor Theorem	Factor Theorem Topic Polynomials Definition The Factor Theorem states that a polynomial p(x) has a factor (x - r) if and only if p(r) = 0. Description The Factor Theorem is a powerful tool in polynomial algebra that bridges the concepts of roots and factors. This theorem provides a method for determining whether a given linear expression is a factor of a polynomial without performing long division. It's particularly useful in finding roots of polynomials and in polynomial factorization.	Factoring Polynomials
Definition--Polynomial Concepts--Factored Cubic	Factored Cubic Polynomial Topic Polynomials Definition A factored cubic polynomial is a third-degree polynomial expressed as the product of its linear factors, typically in the form a(x - r₁)(x - r₂)(x - r₃), where r₁, r₂, and r₃ are the roots of the polynomial.	Factoring Polynomials
Definition--Polynomial Concepts--Factored Polynomial	Factored Polynomial Topic Polynomials Definition A factored polynomial is a polynomial that is expressed as the product of its factors. Description Factoring polynomials is a fundamental skill in algebra that simplifies complex expressions and solves polynomial equations. By expressing a polynomial as the product of its factors, students can more easily identify the roots of the polynomial and understand its behavior. Factored forms are particularly useful in solving quadratic and higher-degree equations.	Factoring Polynomials
Definition--Polynomial Concepts--Factored Quadratic	Factored Quadratic Topic Polynomials Definition A factored quadratic is a second-degree polynomial expressed as the product of its linear factors. Description Factoring quadratic polynomials is a key concept in algebra that simplifies solving quadratic equations and analyzing their properties. A factored quadratic reveals the roots of the equation, which are the x-intercepts of its graph. This form is particularly useful in solving equations, graphing quadratic functions, and understanding the behavior of parabolas.	Factoring Polynomials
Definition--Polynomial Concepts--Factorial	Factorial Topic Polynomials Definition A factorial, denoted by n!, is the product of all positive integers less than or equal to n. Description The factorial function is a fundamental concept in mathematics, particularly in combinatorics, algebra, and calculus. It is denoted by n! and represents the product of all positive integers up to a given number n. Factorials are used to calculate permutations, combinations, and in various mathematical series and functions.	Polynomial Expressions
Definition--Prime and Composite Properties--Common Factors	Common Factors Topic Prime and Composite Numbers Definition Common factors are numbers that are factors of two or more numbers. In the context of prime and composite numbers, common factors can help identify relationships between different numbers. Description Common factors play a significant role in understanding the properties and relationships between prime and composite numbers. A prime number is defined as a number greater than 1 that has no positive divisors other than 1 and itself. In contrast, a composite number has more than two factors, meaning it can be divided evenly by numbers other than 1 and itself.	Prime and Composite Numbers
Definition--Prime and Composite Properties--Factor	Prime and Composite Numbers: Factor Topic Prime and Composite Numbers Definition A factor is a number that divides another number without leaving a remainder. Description Factors play a crucial role in understanding prime and composite numbers. A prime number is defined as a number greater than 1 that has no positive divisors other than 1 and itself. This means a prime number has exactly two distinct factors: 1 and the number itself. For example, the number 7 is prime because its only factors are 1 and 7.	Prime and Composite Numbers
Definition--Prime and Composite Properties--Factor Tree	Factor Tree Topic Prime and Composite Numbers Definition A factor tree is a graphical representation used to determine the prime factors of a composite number by breaking it down into its prime components.	Prime and Composite Numbers
Definition--Prime and Composite Properties--Greatest Common Factor	Greatest Common Factor (GCF) Topic Prime and Composite Numbers Definition The Greatest Common Factor (GCF) of two or more numbers is the largest number that divides all of them without leaving a remainder. Description The concept of the Greatest Common Factor (GCF) is crucial in the study of prime and composite numbers. The GCF helps in simplifying fractions, finding common denominators, and solving problems involving divisibility. Understanding the GCF is essential for grasping more complex mathematical concepts such as least common multiples, prime factorization, and algebraic expressions.	Prime and Composite Numbers
Definition--Prime and Composite Properties--Prime Factor	Prime Factors Topic Prime and Composite Numbers Definition Prime factors are the prime numbers that when multiplied together give a particular result. Description Prime factors play a crucial role in the study of prime and composite numbers. A prime factor is a factor that is a prime number, one of the building blocks of all numbers. For example, the prime factors of 12 are 2 and 3, because 2 • 2 • 3 = 12. Understanding prime factors helps in various mathematical processes such as simplifying fractions, finding the greatest common divisor (GCD), and the least common multiple (LCM).	Prime and Composite Numbers
Definition--Prime and Composite Properties--Prime Factorization	Prime Factorization Topic Prime and Composite Numbers Definition Prime factorization is the process of breaking down a composite number into a product of its prime factors. Description Prime factorization is a fundamental concept in number theory and is essential for understanding the properties of numbers. It involves expressing a composite number as a product of prime numbers, which are numbers greater than 1 that have no divisors other than 1 and themselves. For example, the prime factorization of 28 is 22 • 7, meaning 28 can be broken down into the prime numbers 2 and 7.	Prime and Composite Numbers
Definition--Prime and Composite Properties--Proper Factor	Proper Factors Topic Prime and Composite Numbers Definition Proper factors of a number are all the factors of that number except the number itself and 1. Description Proper factors play a significant role in the study of prime and composite numbers. A prime number is defined as a number greater than 1 that has no proper factors other than itself and 1. This means that prime numbers cannot be divided evenly by any other numbers. For example, the number 7 is a prime number because its only factors are 1 and 7, and it has no proper factors.	Prime and Composite Numbers
Definition--Quadratics Concepts--Quadratic Function in Factored Form	Quadratic Function in Factored Form Topic Quadratics Concepts Definition A quadratic function in factored form is expressed as f(x) = a(x − r1)(x − r2) where r1 and r2 are the roots.	Quadratic Equations and Functions
Definition--Rationals and Radicals--Factoring a Radical	Factoring a Radical Topic Rationals and Radicals Definition Factoring a radical involves expressing it as a product of simpler expressions. Description Factoring radicals is a key technique in the study of Radical Numbers, Expressions, Equations, and Functions. It simplifies complex radical expressions, making them easier to work with. This process is essential for solving equations and for performing algebraic manipulations involving radicals. Understanding how to factor radicals is also important for simplifying expressions in calculus and higher-level mathematics. It helps in breaking down complex problems into more manageable parts.	Radical Functions and Equations
Definition--Ratios, Proportions, and Percents Concepts--Scale Factor	Scale Factor Topic Ratios, Proportions, and Percents Definition A scale factor is a number that scales, or multiplies, some quantity. Description Scale factors are used in various applications, such as resizing images, models, and maps. For instance, if a model car is built at a scale factor of 1:24, it means the model is 1/24th the size of the actual car. This concept is crucial in fields requiring accurate scaling, such as architecture and engineering.	Proportions
Elementary Definition--Multiplication and Division Concepts--Factor	Factor Topic Multiplication and Division Definition A factor is a number that divides another number exactly without leaving a remainder.	Multiplication Expressions and Equations
Factor Bingo Game	A bingo-style game where students identify the factors of numbers I the range 1-20. Note: The download is a PDF file. Related Resources To see the complete Worksheet Library, click on this link: https://media4math.com/worksheet-library	Numerical and Algebraic Expressions
Factor Table, 1-10	A table that lists all the factors for the numbers 1-10. Note: The download is a PDF file. Related Resources To see the complete Worksheet Library, click on this link: https://media4math.com/worksheet-library	Numerical and Algebraic Expressions
Factor Table, 1-20	A table that lists all the factors for the numbers 1-20. Note: The download is a PDF file. Related Resources To see the complete Worksheet Library, click on this link: https://media4math.com/worksheet-library	Numerical and Algebraic Expressions
Factor Table, 1-5	A table that lists all the factors for the numbers 1-5. Note: The download is a PDF file. Related Resources To see the complete Worksheet Library, click on this link: https://media4math.com/worksheet-library	Numerical and Algebraic Expressions
Formulas--Factorial	Formulas--Factorial The formula for Factorial. This is part of a collection of math formulas. To see the complete collection of formulas, click on this link. Note: The download is a JPG file. Related Resources To see resources related to this topic click on the Related Resources tab above.	Numerical Expressions
INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Factored Form	INSTRUCTIONAL RESOURCE: Tutorial: Analyzing Graphs of Quadratic Functions in Factored Form This slide show provides 8 examples of quadratic functions in factored form and analyzes their graphs. This is part of a collection of tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Note: The download is a PPT file. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Quadratic Equations and Functions
INSTRUCTIONAL RESOURCE: Tutorial: Multiples and Factors	INSTRUCTIONAL RESOURCE: Tutorial: Multiples and Factors This tutorial provides an overview of multiples and factors. This includes an exploration of generating multiples by skip-counting. This is part of a collection of math tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Complete Number Patterns
INSTRUCTIONAL RESOURCE: Tutorial: Simplifying Fractions Using the GCF	INSTRUCTIONAL RESOURCE: Tutorial: Simplifying Fractions Using the GCF In this tutorial students are shown how to find the GCF of the numerator and denominator and how to use it to simplify a fraction. Note: The download is a PDF version of this tutorial. This is part of a collection of math tutorials on a variety of math topics. To see the complete collection of these resources, click on this link. Library of Instructional Resources To see the complete library of Instructional Resources , click on this link.	Find Greatest Common Factors and Write Fractions in Lowest Terms