Illustrative Math Alignment: Grade 6 Unit 8

Topic

Measures of Central Tendency

Description

This example illustrates the calculation of a weighted mean using a collection of coins with different values. The image shows pennies, nickels, dimes, and quarters stacked in columns, representing quantities of 4, 3, 5, and 2 respectively. The weighted mean is computed using the formula: (4 * 1 + 3 * 5 + 5 * 10 + 2 * 25) / (4 + 3 + 5 + 2), resulting in an average value of 8.5 cents.

Topic

Measures of Central Tendency

Description

This example demonstrates the calculation of a weighted mean in the context of probability, specifically finding the average sum when rolling two fair dice. The image displays a grid showing all possible outcomes of rolling two dice, with sums ranging from 2 to 12. The frequencies of each sum are highlighted in red, serving as the weights in the weighted mean calculation. The weighted mean is computed using the formula: (2 * 1 + 3 * 2 + 4 * 3 + 5 * 4 + 6 * 5 + 7 * 6 + 8 * 5 + 9 * 4 + 10 * 3 + 11 * 2 + 12 * 1) / 36, resulting in an average sum of 7.

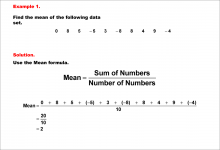
Topic

Measures of Central Tendency

Description

This math example demonstrates the calculation of the mean for a data set that includes negative numbers: 0, 8, 5, -5, 3, -8, 8, 4, 9, -4. The example emphasizes the step-by-step process of finding the mean, showing how to handle both positive and negative values in the calculation.

Topic

Measures of Central Tendency

Description

This example illustrates the calculation of the mean for a dataset containing both positive and negative numbers: 7, 4, 1, 1, -1, -2, 9, 4, -9, -4. The step-by-step process shows how to sum all values, including negative ones, and divide by the total number of data points to find the mean.

Topic

Measures of Central Tendency

Description

This example demonstrates the calculation of the mean for a dataset that includes negative numbers and zeros: 4, -1, 0, -2, -9, 0, -6, 5, 0, -1. The step-by-step process illustrates how to sum all values, including negatives and zeros, and divide by the total number of data points to determine the mean.

Topic

Measures of Central Tendency

Description

This example illustrates the calculation of the mean for a dataset containing both positive and negative numbers: -3, 8, 2, 1, 3, -6, -9, 3, -4. The step-by-step process demonstrates how to sum all values, including negative ones, and divide by the total number of data points to find the mean.

Topic

Measures of Central Tendency

Description

This example demonstrates the calculation of the mean for a dataset that includes both positive and negative numbers: -1, 9, 3, 3, 6, -8, 8, 1, 4, 5. The step-by-step process shows how to sum all values, including negative ones, and divide by the total number of data points to determine the mean.

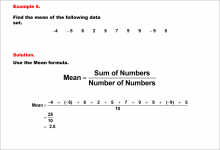
Topic

Measures of Central Tendency

Description

This example illustrates the calculation of the mean for a dataset containing both positive and negative numbers: -4, -5, 6, 2, 5, 7, 9, 9, -9, 5. The step-by-step process demonstrates how to sum all values, including negative ones, and divide by the total number of data points to find the mean.

Topic

Measures of Central Tendency

Description

This example demonstrates the calculation of the mean for a dataset that includes negative numbers and zero: -4, 0, 2, 9, -2, -3, -5, 10, -7, 5. The step-by-step process illustrates how to sum all values, including negatives and zero, and divide by the total number of data points to determine the mean.

Topic

Measures of Central Tendency

Description

This image shows a math example calculating the mean of a data set. The numbers are: 4, 8, -6, -6, 6, -3, 4, -8, -6, -8. The solution uses the mean formula. Example 8 demonstrates finding the mean of the data set. The mean is calculated by summing all numbers and dividing by the count of numbers, resulting in (-15) / (10) = -1.5.

Topic

Measures of Central Tendency

Description

The image shows Example 9, illustrating how to find the mean of a data set using the mean formula. This example demonstrates finding the mean of the data set: -8, -9, 10, -2, 3, -2, -8, -3, 2, 5. The calculation is shown step-by-step: Mean = Sum / Count. The sum of all numbers (-8 + (-9) + 10 + (-2) + 3 + (-2) + (-8) + (-3) + 2 + 5) is divided by the count of numbers (10), resulting in -12 / 10 = -1.2.

Topic

Measures of Central Tendency

Description

The image shows Example 10, demonstrating how to calculate the mean for a different set of numbers. This example illustrates finding the mean of the data set: -6, 5, -5, -5, -7, -7, -4, -1, 3. The calculation is presented step-by-step: Mean = Sum / Count. The sum of all numbers (-6 + 5 + (-5) + (-5) + (-7) + (-7) + (-4) + (-1) + 3) is divided by the count of numbers (10), resulting in -34 / 10 = -3.4.

In this drag-and-drop game, have students practice their skills at calculating the median of a data set. This game generates thousands of different combinations, offering an ideal opportunity for skill review in a game format.

Note: The download is the Teacher's Guide.

In this drag-and-drop game, have students practice their skills at calculating the mean of a data set. This game generates thousands of different combinations, offering an ideal opportunity for skill review in a game format.

Related Resources

In this TI Nspire tutorial, the Spreadsheet and Calculator windows are used to find the mean of a data list. This video supports the TI-Nspire Clickpad and Touchpad. This Mini-Tutorial Video includes a worksheet. .

This is the transcript for the TI-Nspire Mini-Tutorial entitled, Finding the Mean of a Data List.

To see the complete collection of video transcriptsy, click on this link.

In this video tutorial students learn about the mean of a probability distribution. Includes a brief discussion of expected value, plus a brief tie-in to weighted means. Includes three real-world examples.

In this video tutorial students learn about sample mean from a random sampling of data. All examples involve normally distributed data with a known population mean and standard deviation. Includes three real-world examples.

In this video tutorial students learn about normally distributed data and how to identify the population mean from the normal distribution. Standard deviation is briefly introduced. Includes three real-world examples.

In this video tutorial students learn how to calculate the mode of a data set, as well as how the mode differs from the mean and median.Includes three real-world examples.

In this video tutorial students extend their understanding of mean by looking at examples of weighted means (sometimes referred to as weighted averages). Includes three real-world examples.

In this video tutorial students learn how to find the median of a data set. The mean is also calculated so that students can learn similarities and differences between these two measures of central tendency. Includes three real-world examples.

In this video tutorial students learn how to calculate the mean when some of the data items are negative numbers. Includes three real-world examples.

In this video tutorial students learn how to calculate the mean when all of the data items are positive numbers. Includes three real-world examples.

This is the transcript for the video entitled, "Video Tutorial: Measures of Central Tendency: Mean of a Probability Distribution."

To see the complete collection of video transcriptsy, click on this link.

Topic

Measures of Central Tendency

Description

This section introduces the mean of probability distributions, also known as expected value, showing its calculation and interpretation in scenarios like dice rolls and coin flips. Key terms include mean, probability distribution, expected value, and weighted mean.

This is the transcript for the video entitled, "Video Tutorial: Measures of Central Tendency: Sample Mean."

To see the complete collection of video transcriptsy, click on this link.

Topic

Measures of Central Tendency

Description

The video explains the sample mean and standard error, illustrating how they estimate population characteristics. Examples include trout lengths, macaw wingspans, and elephant weights. Key terms include sample mean, standard error, population mean, and summation.

This is the transcript for the video entitled, "Video Tutorial: Measures of Central Tendency: The Mean and Normally Distributed Data."

To see the complete collection of video transcriptsy, click on this link.

Topic

Measures of Central Tendency

Description

This video examines the mean in normally distributed data, linking it to standard deviation and probabilities. Examples include batting averages, heights, and shoe sizes, emphasizing normal distribution properties. Key terms include mean, normal distribution, standard deviation, and probabilities.

This is the transcript for the video entitled, "Video Tutorial: Measures of Central Tendency: Finding the Mode of a Data Set."

To see the complete collection of video transcriptsy, click on this link.

Topic

Measures of Central Tendency

Description

This section focuses on the mode, the most frequent value in a data set, and its applications in dice rolls, beverage ratings, and color preferences. It compares mode with mean and median, highlighting its utility in categorical data. Key terms include mode, frequency, and categorical data.

This is the transcript for the video entitled, "Video Tutorial: Measures of Central Tendency: Weighted Mean."

To see the complete collection of video transcriptsy, click on this link.

Topic

Measures of Central Tendency

Description

The video introduces the weighted mean for data sets with different item frequencies, using examples like cylinder heights, kettlebell weights, and daycare ages. It compares weighted means to medians to show their practical applications. Key terms include weighted mean, weights, and frequency.

This is the transcript for the video entitled, "Video Tutorial: Measures of Central Tendency: Finding the Median of a Data Set."

To see the complete collection of video transcriptsy, click on this link.

Topic

Measures of Central Tendency

Description

This segment discusses the median, another measure of central tendency, focusing on its calculation by ordering data and finding the middle value. Examples include test scores, basketball player heights, and family ages, highlighting scenarios where the median differs from the mean. Key terms include median, middle value, and ordering.

This is the transcript for the video entitled, "Video Tutorial: Measures of Central Tendency: Finding the Mean of a Data Set II."

To see the complete collection of video transcriptsy, click on this link.

Topic

Measures of Central Tendency

Description

The video explores calculating the mean with data sets including negative numbers, like temperatures in Fairbanks and Fargo, and tide heights in Gloucester. It emphasizes the mean's robustness across varying data types and scenarios. Key terms include negative numbers, sum, and ratio.

This is the transcript for the video entitled, "Video Tutorial: Measures of Central Tendency: Finding the Mean of a Data Set I."

To see the complete collection of video transcriptsy, click on this link.

Topic

Measures of Central Tendency

Description

This video introduces the mean as a measure of central tendency, explaining it as the sum of values divided by their count. Examples include calculating test scores, flamingo wingspans, and football punt lengths, demonstrating how the mean is applied to summarize data. Key terms include mean, average, sum, and ratio.

Topic

Statistics

Definition

The outlier is is an extreme value for a data set.

Description

The Outlier is an important concept in statistics. While it doesn't represent the average data set, it does set the range of extreme values in the data set. An outlier can be extremely large or small. 

In mathematics education, understanding outlier is crucial as it lays the foundation for more advanced statistical concepts. It allows students to grasp the significance of data analysis and interpretation. In classes, students often perform exercises calculating the mean of sets, which enhances their understanding of averaging techniques.

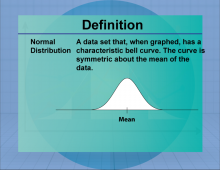
Topic

Statistics

Definition

The normal distribution is a measure of central tendency that provides an average representation of a set of data.

Description

The Normal Distribution is an important concept in statistics, used to summarize data effectively. In real-world applications, the Normal Distribution helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research.

Topic

Statistics

Definition

Categorical data refers to data that can be divided into specific categories or groups.

Description

Categorical data is essential for organizing and analyzing information that falls into distinct categories, such as gender, race, or product type. This type of data is often used in market research, social sciences, and public health studies to identify patterns and relationships between groups. In mathematics, understanding categorical data is crucial for interpreting bar charts, pie charts, and frequency tables.

Topic

Statistics

Definition

A probability distribution describes how the values of a random variable are distributed.

Description

Probability distributions are fundamental in statistics, providing a mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. They are used in various fields such as finance, science, and engineering to model uncertainty and variability. For instance, the normal distribution is a common probability distribution that describes many natural phenomena.

Topic

Statistics

Definition

The measures of central tendency is a measure of central tendency that provides an average representation of a set of data.

Description

The Measures of Central Tendency is an important concept in statistics, used to summarize data effectively.

In real-world applications, the Measures of Central Tendency helps to interpret data distributions and is widely used in areas such as economics, social sciences, and research.

For example, if a data set consists of the values 2, 3, and 10, the mean is calculated as (2 + 3 + 10)/3 = 5.

This set of 10 Quizlet Flashcards covers the topic of finding the Mean of a data set.

Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards.

Related Resources

To see other resources related to this topic, click on the Resources tab above.

Quizlet Library

To see the complete Quizlet Flash Card Library, click on this Link to see the collection.

This set of 10 Quizlet Flashcards covers the topic of finding the Mean of a data set.

Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards.

Related Resources

To see other resources related to this topic, click on the Resources tab above.

Quizlet Library

To see the complete Quizlet Flash Card Library, click on this Link to see the collection.

This set of 10 Quizlet Flashcards covers the topic of finding the Mean of a data set.

Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards.

Related Resources

To see other resources related to this topic, click on the Resources tab above.

Quizlet Library

To see the complete Quizlet Flash Card Library, click on this Link to see the collection.

This set of 10 Quizlet Flashcards covers the topic of finding the Mean of a data set.

Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards.

Related Resources

To see other resources related to this topic, click on the Resources tab above.

Quizlet Library

To see the complete Quizlet Flash Card Library, click on this Link to see the collection.

This set of 10 Quizlet Flashcards covers the topic of finding the Mean of a data set.

Note: The download is the teacher's guide for using Media4Math's Quizlet Flash Cards.

Related Resources

To see other resources related to this topic, click on the Resources tab above.

Quizlet Library

To see the complete Quizlet Flash Card Library, click on this Link to see the collection.