
Illustrative Math Alignment: Grade 6 Unit 9
Putting it All Together
Lesson 4: How Do We Choose?
Use the following Media4Math resources with this Illustrative Math lesson.
| Thumbnail Image | Title | Body | Curriculum Topics |
|---|---|---|---|

|
Math Clip Art--The Language of Math--Numbers and Operations 14 | Math Clip Art--The Language of Math--Numbers and Operations 14TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 14+5. It serves as a crucial tool in teaching addition and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "14+5" and its written form, students can more easily grasp the concept of addition and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 15 | Math Clip Art--The Language of Math--Numbers and Operations 15TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 15+6. It serves as a valuable tool in teaching addition and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "15+6" alongside its written form, students can more easily grasp the concept of addition and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 16 | Math Clip Art--The Language of Math--Numbers and Operations 16TopicThe Language of Math DescriptionThis image presents the numerical expression and corresponding words for 1-1. It's an invaluable resource for teaching subtraction and strengthening the link between mathematical notation and verbal expression. By showcasing "1-1" visually alongside its written form, students can more easily understand how subtraction is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 17 | Math Clip Art--The Language of Math--Numbers and Operations 17TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 2-1. It serves as a crucial tool in teaching subtraction and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "2-1" and its written form, students can more easily grasp the concept of subtraction and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
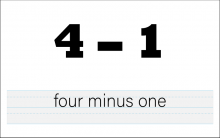
Math Clip Art--The Language of Math--Numbers and Operations 18 | Math Clip Art--The Language of Math--Numbers and Operations 18TopicThe Language of Math DescriptionThis image showcases the numerical expression and corresponding words for 3-1. It's an essential tool for teaching subtraction and reinforcing the link between mathematical notation and verbal expression. By presenting "3-1" visually alongside its written form, students can more easily understand how subtraction is expressed both numerically and verbally. |
Number Names and Numerical Expressions |
|
Math Clip Art--The Language of Math--Numbers and Operations 19 | Math Clip Art--The Language of Math--Numbers and Operations 19TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 4-1. It serves as a valuable tool in teaching subtraction and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "4-1" alongside its written form, students can more easily grasp the concept of subtraction and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 20 | Math Clip Art--The Language of Math--Numbers and Operations 20TopicThe Language of Math DescriptionThis image presents the numerical expression and corresponding words for 5-1. It's an invaluable resource for teaching subtraction and strengthening the link between mathematical notation and verbal expression. By showcasing "5-1" visually alongside its written form, students can more easily understand how subtraction is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 21 | Math Clip Art--The Language of Math--Numbers and Operations 21TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 6-2. It serves as a crucial tool in teaching subtraction and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "6-2" and its written form, students can more easily grasp the concept of subtraction and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 22 | Math Clip Art--The Language of Math--Numbers and Operations 22TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 7-1. It serves as a valuable tool in teaching subtraction and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "7-1" alongside its written form, students can more easily grasp the concept of subtraction and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 23 | Math Clip Art--The Language of Math--Numbers and Operations 23TopicThe Language of Math DescriptionThis image presents the numerical expression and corresponding words for 8-3. It's an invaluable resource for teaching subtraction and strengthening the link between mathematical notation and verbal expression. By showcasing "8-3" visually alongside its written form, students can more easily understand how subtraction is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 24 | Math Clip Art--The Language of Math--Numbers and Operations 24TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 9-5. It serves as a crucial tool in teaching subtraction and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "9-5" and its written form, students can more easily grasp the concept of subtraction and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 25 | Math Clip Art--The Language of Math--Numbers and Operations 25TopicThe Language of Math DescriptionThis image showcases the numerical expression and corresponding words for 10-1. It's an essential tool for teaching subtraction and reinforcing the link between mathematical notation and verbal expression. By presenting "10-1" visually alongside its written form, students can more easily understand how subtraction is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 26 | Math Clip Art--The Language of Math--Numbers and Operations 26TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 11-2. It serves as a valuable tool in teaching subtraction and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "11-2" alongside its written form, students can more easily grasp the concept of subtraction and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 27 | Math Clip Art--The Language of Math--Numbers and Operations 27TopicThe Language of Math DescriptionThis image presents the numerical expression and corresponding words for 12-3. It's an invaluable resource for teaching subtraction and strengthening the link between mathematical notation and verbal expression. By showcasing "12-3" visually alongside its written form, students can more easily understand how subtraction is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 28 | Math Clip Art--The Language of Math--Numbers and Operations 28TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 13-4. It serves as a crucial tool in teaching subtraction and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "13-4" and its written form, students can more easily grasp the concept of subtraction and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 29 | Math Clip Art--The Language of Math--Numbers and Operations 29TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 14-5. It serves as a crucial tool in teaching subtraction and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "14-5" and its written form, students can more easily grasp the concept of subtraction and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 30 | Math Clip Art--The Language of Math--Numbers and Operations 30TopicThe Language of Math DescriptionThis image showcases the numerical expression and corresponding words for 15-6. It's an essential tool for teaching subtraction and reinforcing the link between mathematical notation and verbal expression. By presenting "15-6" visually alongside its written form, students can more easily understand how subtraction is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 31 | Math Clip Art--The Language of Math--Numbers and Operations 31TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 1*1. It serves as a valuable tool in teaching multiplication and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "1*1" alongside its written form, students can more easily grasp the concept of multiplication and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 32 | Math Clip Art--The Language of Math--Numbers and Operations 32TopicThe Language of Math DescriptionThis image presents the numerical expression and corresponding words for 2*1. It's an invaluable resource for teaching multiplication and strengthening the link between mathematical notation and verbal expression. By showcasing "2*1" visually alongside its written form, students can more easily understand how multiplication is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 33 | Math Clip Art--The Language of Math--Numbers and Operations 33TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 3*1. It serves as a crucial tool in teaching multiplication and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "3*1" and its written form, students can more easily grasp the concept of multiplication and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 34 | Math Clip Art--The Language of Math--Numbers and Operations 34TopicThe Language of Math DescriptionThis image showcases the numerical expression and corresponding words for 4*1. It's an essential tool for teaching multiplication and reinforcing the link between mathematical notation and verbal expression. By presenting "4*1" visually alongside its written form, students can more easily understand how multiplication is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 35 | Math Clip Art--The Language of Math--Numbers and Operations 35TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 5*1. It serves as a valuable tool in teaching multiplication and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "5*1" alongside its written form, students can more easily grasp the concept of multiplication and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 36 | Math Clip Art--The Language of Math--Numbers and Operations 36TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 6*2. It serves as a valuable tool in teaching multiplication and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "6*2" alongside its written form, students can more easily grasp the concept of multiplication and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 37 | Math Clip Art--The Language of Math--Numbers and Operations 37TopicThe Language of Math DescriptionThis image presents the numerical expression and corresponding words for 7*3. It's an invaluable resource for teaching multiplication and strengthening the link between mathematical notation and verbal expression. By showcasing "7*3" visually alongside its written form, students can more easily understand how multiplication is expressed both numerically and verbally. |
Number Names and Numerical Expressions |
|
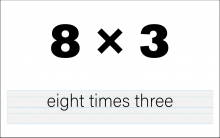
Math Clip Art--The Language of Math--Numbers and Operations 38 | Math Clip Art--The Language of Math--Numbers and Operations 38TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 8*3. It serves as a crucial tool in teaching multiplication and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "8*3" and its written form, students can more easily grasp the concept of multiplication and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 39 | Math Clip Art--The Language of Math--Numbers and Operations 39TopicThe Language of Math DescriptionThis image showcases the numerical expression and corresponding words for 9*5. It's an essential tool for teaching multiplication and reinforcing the link between mathematical notation and verbal expression. By presenting "9*5" visually alongside its written form, students can more easily understand how multiplication is expressed both numerically and verbally. |
Number Names and Numerical Expressions |
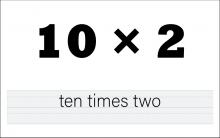
|
Math Clip Art--The Language of Math--Numbers and Operations 40 | Math Clip Art--The Language of Math--Numbers and Operations 40TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 10*2. It serves as a valuable tool in teaching multiplication and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "10*2" alongside its written form, students can more easily grasp the concept of multiplication and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |
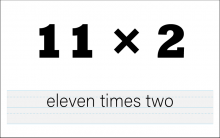
|
Math Clip Art--The Language of Math--Numbers and Operations 41 | Math Clip Art--The Language of Math--Numbers and Operations 41TopicThe Language of Math DescriptionThis image presents the numerical expression and corresponding words for 11*2. It's an invaluable resource for teaching multiplication and strengthening the link between mathematical notation and verbal expression. By showcasing "11*2" visually alongside its written form, students can more easily understand how multiplication is expressed both numerically and verbally. |
Number Names and Numerical Expressions |
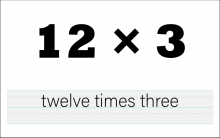
|
Math Clip Art--The Language of Math--Numbers and Operations 42 | Math Clip Art--The Language of Math--Numbers and Operations 42TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 12*3. It serves as a crucial tool in teaching multiplication and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "12*3" and its written form, students can more easily grasp the concept of multiplication and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |
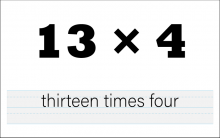
|
Math Clip Art--The Language of Math--Numbers and Operations 43 | Math Clip Art--The Language of Math--Numbers and Operations 43TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 13*4. It serves as a valuable tool in teaching multiplication and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "13*4" alongside its written form, students can more easily grasp the concept of multiplication and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |
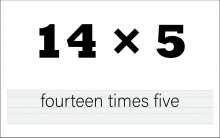
|
Math Clip Art--The Language of Math--Numbers and Operations 44 | Math Clip Art--The Language of Math--Numbers and Operations 44TopicThe Language of Math DescriptionThis image presents the numerical expression and corresponding words for 14*5. It's an invaluable resource for teaching multiplication and strengthening the link between mathematical notation and verbal expression. By showcasing "14*5" visually alongside its written form, students can more easily understand how multiplication is expressed both numerically and verbally. |
Number Names and Numerical Expressions |
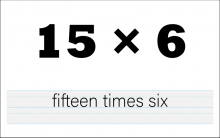
|
Math Clip Art--The Language of Math--Numbers and Operations 45 | Math Clip Art--The Language of Math--Numbers and Operations 45TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 15*6. It serves as a crucial tool in teaching multiplication and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "15*6" and its written form, students can more easily grasp the concept of multiplication and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 46 | Math Clip Art--The Language of Math--Numbers and Operations 46TopicThe Language of Math DescriptionThis image showcases the numerical expression and corresponding words for 1/1. It's an essential tool for teaching division and reinforcing the link between mathematical notation and verbal expression. By presenting "1/1" visually alongside its written form, students can more easily understand how division is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 47 | Math Clip Art--The Language of Math--Numbers and Operations 47TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 2/1. It serves as a valuable tool in teaching division and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "2/1" alongside its written form, students can more easily grasp the concept of division and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 48 | Math Clip Art--The Language of Math--Numbers and Operations 48TopicThe Language of Math DescriptionThis image presents the numerical expression and corresponding words for 3/1. It's an invaluable resource for teaching division and strengthening the link between mathematical notation and verbal expression. By showcasing "3/1" visually alongside its written form, students can more easily understand how division is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 49 | Math Clip Art--The Language of Math--Numbers and Operations 49TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 4/1. It serves as a crucial tool in teaching division and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "4/1" and its written form, students can more easily grasp the concept of division and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 50 | Math Clip Art--The Language of Math--Numbers and Operations 50TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 5/1. It serves as a valuable tool in teaching division and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "5/1" alongside its written form, students can more easily grasp the concept of division and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 51 | Math Clip Art--The Language of Math--Numbers and Operations 51TopicThe Language of Math DescriptionThis image presents the numerical expression and corresponding words for 6/2. It's an invaluable resource for teaching division and strengthening the link between mathematical notation and verbal expression. By showcasing "6/2" visually alongside its written form, students can more easily understand how division is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 52 | Math Clip Art--The Language of Math--Numbers and Operations 52TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 7/3. It serves as a crucial tool in teaching division and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "7/3" and its written form, students can more easily grasp the concept of division and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 53 | Math Clip Art--The Language of Math--Numbers and Operations 53TopicThe Language of Math DescriptionThis image showcases the numerical expression and corresponding words for 8/3. It's an essential tool for teaching division and reinforcing the link between mathematical notation and verbal expression. By presenting "8/3" visually alongside its written form, students can more easily understand how division is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 54 | Math Clip Art--The Language of Math--Numbers and Operations 54TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 9/5. It serves as a valuable tool in teaching division and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "9/5" alongside its written form, students can more easily grasp the concept of division and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 55 | Math Clip Art--The Language of Math--Numbers and Operations 55TopicThe Language of Math DescriptionThis image presents the numerical expression and corresponding words for 10/2. It's an invaluable resource for teaching division and strengthening the link between mathematical notation and verbal expression. By showcasing "10/2" visually alongside its written form, students can more easily understand how division is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 56 | Math Clip Art--The Language of Math--Numbers and Operations 56TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 11/2. It serves as a crucial tool in teaching division and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "11/2" and its written form, students can more easily grasp the concept of division and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 57 | Math Clip Art--The Language of Math--Numbers and Operations 57TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 12/3. It serves as a crucial tool in teaching division and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual link between "12/3" and its written form, students can more easily grasp the concept of division and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 58 | Math Clip Art--The Language of Math--Numbers and Operations 58TopicThe Language of Math DescriptionThis image showcases the numerical expression and corresponding words for 13/4. It's an essential tool for teaching division and reinforcing the link between mathematical notation and verbal expression. By presenting "13/4" visually alongside its written form, students can more easily understand how division is expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 59 | Math Clip Art--The Language of Math--Numbers and Operations 59TopicThe Language of Math DescriptionThis image illustrates the numerical expression and corresponding words for 14/5. It serves as a valuable tool in teaching division and reinforcing the connection between mathematical symbols and their verbal representations. By providing a visual representation of "14/5" alongside its written form, students can more easily grasp the concept of division and how it's expressed both numerically and verbally. |
Number Names and Numerical Expressions |

|
Math Clip Art--The Language of Math--Numbers and Operations 60 | Math Clip Art--The Language of Math--Numbers and Operations 60TopicThe Language of Math DescriptionThis image presents the numerical expression and corresponding words for 15/6. It's an invaluable resource for teaching division and strengthening the link between mathematical notation and verbal expression. By showcasing "15/6" visually alongside its written form, students can more easily understand how division is expressed both numerically and verbally. |
Number Names and Numerical Expressions |
|
Math Clip Art--The Language of Math--Numbers and Operations 61 | Math Clip Art--The Language of Math--Numbers and Operations 61TopicThe Language of Math DescriptionThis image shows a blank card, which is part of a series of 61 clip art images focused on the language of math and numbers and operations. While it doesn't display a specific mathematical expression, it serves an important purpose in the collection. This blank card can be used creatively by teachers and students to create their own mathematical expressions, encouraging active engagement and personalized learning. |
Number Names and Numerical Expressions |

|
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 01 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 01TopicQuadratics DescriptionThis image features a vintage car in motion with a blurred background, emphasizing speed. It serves as an introduction to the series on speed and acceleration in linear and quadratic functions. The image visually represents the concept of speed through motion blur, making it relatable for students learning about linear functions. By using this image, teachers can engage students with real-world applications of mathematical concepts. |
Graphs of Linear Functions and Graphs of Quadratic Functions |
|
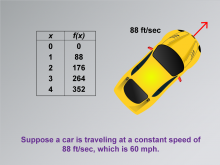
Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 02 | Math Clip Art--Applications of Linear and Quadratic Functions: Speed and Acceleration 02TopicQuadratics DescriptionThis image depicts a yellow car alongside a table that shows time in seconds and distance in feet, illustrating a constant speed of 88 ft/sec (60 mph). The table provides a clear example of how linear functions can represent constant speeds. Teachers can use this image to demonstrate the relationship between time, distance, and speed, reinforcing the concept of constant rates within linear functions. |
Graphs of Linear Functions and Graphs of Quadratic Functions |