Illustrative Math Alignment: Grade 6 Unit 9

Putting it All Together

Lesson 4: How Do We Choose?

Use the following Media4Math resources with this Illustrative Math lesson.

Title	Body	Curriculum Topics
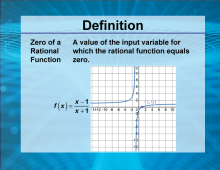
Video Definition 47--Rationals and Radicals--Zero of a Rational Function	Video Definition 47--Rationals and Radicals--Zero of a Rational Function Topic Rationals and Radicals Description The Zero of a Rational Function is the value of the input variable for which the rational function equals zero. For example, in f(x) = (x - 1)/(x + 1), the zero occurs at x = 1. This term highlights the connection between the numerator of a rational function and its roots, which are essential for solving equations involving rational expressions.	Rational Functions and Equations
Video Definition 14--Fraction Concepts--Fraction Operation	Video Definition 14--Fraction Concepts--Fraction Operation Topic Fractions Description Fraction operations include addition, subtraction, multiplication, and division. Examples include 1/2 + 1/3 = 5/6, 3/4 - 1/4 = 1/2. These operations require finding a common denominator for addition/subtraction or applying direct multiplication/division for the respective operations. This encapsulates the arithmetic procedures involving fractions, forming the basis for more complex problem-solving.	Fractions and Mixed Numbers
Video Definition 20--Fraction Concepts--Irrational Number	Video Definition 20--Fraction Concepts--Irrational Number Topic Fractions Description An irrational number cannot be expressed as a fraction and has a non-terminating, non-repeating decimal form. Examples include π = 3.14159... and √2 = 1.41421.... This highlights the contrast between rational and irrational numbers. This connects fractions to the broader number system, emphasizing differences in numerical properties.	Fractions and Mixed Numbers
Video Definition 32--Fraction Concepts--Ratio	Video Definition 32--Fraction Concepts--Ratio Topic Fractions Description A ratio is a comparison of two quantities or numbers by division, often written as a fraction. The image defines it as a / b, where b ≠ 0, and provides examples like 1 / 2 and 2 / 3. This term bridges fractions and their use in comparing quantities, which helps learners connect fraction concepts to real-world applications such as proportions and rates.	Fractions and Mixed Numbers
Video Definition 33--Fraction Concepts--Rational Number	Video Definition 33--Fraction Concepts--Rational Number Topic Fractions Description A rational number is defined as a ratio of two integers that can be expressed as a fraction, whole number, or decimal. Examples provided in the image include 0.5, 1 / 4, and 10. The term builds on the concept of ratios and fractions by showing that they can also represent rational numbers, broadening the application of fractions to include whole numbers and decimals.	Fractions and Mixed Numbers
Video Definition 32--Polynomial Concepts--Rational Root Theorem (Spanish Audio)	Video Definition 32--Polynomial Concepts--Rational Root Theorem (Spanish Audio) Topic Polynomials Description Rational Root Theorem: For a polynomial P(x) with integer coefficients, if it has rational roots, they will be of the form ±p/q, where p is a factor of the constant term and q is a factor of the leading coefficient. Example: P(x) = 2x3 + x2 - 13x + 6. Introduces a systematic way to identify potential rational roots of a polynomial.	Factoring Polynomials
Video Definition 32--Polynomial Concepts--Rational Root Theorem	Video Definition 32--Polynomial Concepts--Rational Root Theorem Topic Polynomials Description Rational Root Theorem: For a polynomial P(x) with integer coefficients, if it has rational roots, they will be of the form ±p/q, where p is a factor of the constant term and q is a factor of the leading coefficient. Example: P(x) = 2x3 + x2 - 13x + 6. Introduces a systematic way to identify potential rational roots of a polynomial.	Factoring Polynomials
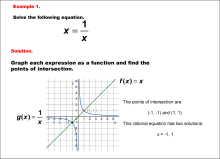
Math Example--Graphical Solutions to Rational Equations--Example 1	This is part of a collection of math examples that show how to use graphical techniques to solve rational equations. Note: The download is an image file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Create a Slide Show Subscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link: Accessibility This resource can also be used with a screen reader.	Rational Functions and Equations
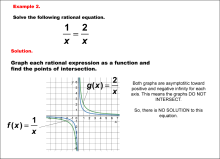
Math Example--Graphical Solutions to Rational Equations--Example 2	This is part of a collection of math examples that show how to use graphical techniques to solve rational equations. Note: The download is an image file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Create a Slide Show Subscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link: Accessibility This resource can also be used with a screen reader.	Rational Functions and Equations
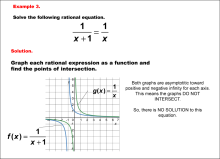
Math Example--Graphical Solutions to Rational Equations--Example 3	This is part of a collection of math examples that show how to use graphical techniques to solve rational equations. Note: The download is an image file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Create a Slide Show Subscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link: Accessibility This resource can also be used with a screen reader.	Rational Functions and Equations
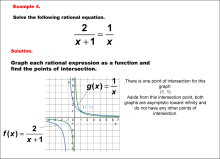
Math Example--Graphical Solutions to Rational Equations--Example 4	This is part of a collection of math examples that show how to use graphical techniques to solve rational equations. Note: The download is an image file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Create a Slide Show Subscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link: Accessibility This resource can also be used with a screen reader.	Rational Functions and Equations
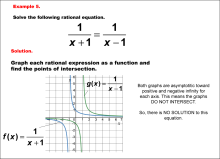
Math Example--Graphical Solutions to Rational Equations--Example 5	This is part of a collection of math examples that show how to use graphical techniques to solve rational equations. Note: The download is an image file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Create a Slide Show Subscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link: Accessibility This resource can also be used with a screen reader.	Rational Functions and Equations
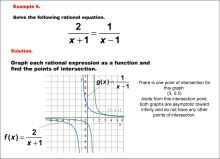
Math Example--Graphical Solutions to Rational Equations--Example 6	This is part of a collection of math examples that show how to use graphical techniques to solve rational equations. Note: The download is an image file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Create a Slide Show Subscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link: Accessibility This resource can also be used with a screen reader.	Rational Functions and Equations
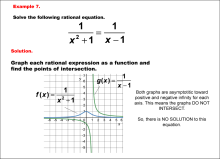
Math Example--Graphical Solutions to Rational Equations--Example 7	This is part of a collection of math examples that show how to use graphical techniques to solve rational equations. Note: The download is an image file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Create a Slide Show Subscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link: Accessibility This resource can also be used with a screen reader.	Rational Functions and Equations
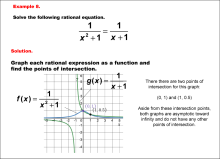
Math Example--Graphical Solutions to Rational Equations--Example 8	This is part of a collection of math examples that show how to use graphical techniques to solve rational equations. Note: The download is an image file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Create a Slide Show Subscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link: Accessibility This resource can also be used with a screen reader.	Rational Functions and Equations
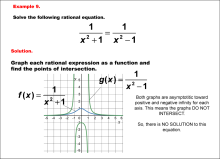
Math Example--Graphical Solutions to Rational Equations--Example 9	This is part of a collection of math examples that show how to use graphical techniques to solve rational equations. Note: The download is an image file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Create a Slide Show Subscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link: Accessibility This resource can also be used with a screen reader.	Rational Functions and Equations
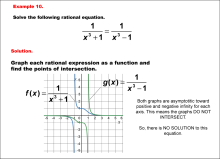
Math Example--Graphical Solutions to Rational Equations--Example 10	This is part of a collection of math examples that show how to use graphical techniques to solve rational equations. Note: The download is an image file. Related Resources To see additional resources on this topic, click on the Related Resources tab. Create a Slide Show Subscribers can use Slide Show Creator to create a slide show from the complete collection of math examples on this topic. To see the complete clip art collection, click on this Link. To learn more about Slide Show Creator, click on this Link: Accessibility This resource can also be used with a screen reader.	Rational Functions and Equations
Definition--Vector Concepts--Vector Quantity: Acceleration	Definition--Vector Concepts--Vector Quantity: Acceleration This is part of a collection of definitions on the topic of Vectors. —Click on PREVIEW to see the definition card.—	Vectors
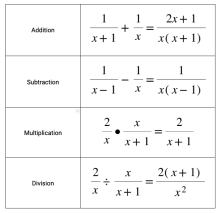
Instructional Resource: Tutorial: What Are Rational Expressions?	Instructional Resource: Tutorial: What Are Rational Expressions? In this tutorial students learn about rational expressions and use the properties of fractions to combine them. —Press PREVIEW to see the tutorial—	Rational Expressions
Definition--Calculus Topics--Acceleration	Definition--Calculus Topics--Acceleration Topic Calculus Definition Acceleration is the rate of change of velocity with respect to time. It is the second derivative of position with respect to time. Description Acceleration is a fundamental concept in calculus, particularly in the study of motion and kinematics. It's crucial for understanding how objects move and change speed over time. In real-world applications, acceleration is used extensively in physics and engineering, from designing roller coasters to launching spacecraft. For example, in automotive engineering, understanding acceleration helps in designing safer vehicles and more efficient engines.	Calculus Vocabulary
Definition--Calculus Topics--Derivative of a Rational Function	Definition--Calculus Topics--Derivative of a Rational Function Topic Calculus Definition The derivative of a rational function f(x) = P(x)/Q(x), where P(x) and Q(x) are polynomials and Q(x) ≠ 0, is given by the quotient rule: f'(x) = (Q(x)P'(x) - P(x)Q'(x)) / [Q(x)]2. Description The derivative of rational functions is a fundamental concept in calculus with significant applications in various fields of science and engineering. It's particularly useful in analyzing rates of change in complex systems, solving differential equations, and optimizing processes in fields like economics, physics, and engineering.	Calculus Vocabulary
Definition--Calculus Topics--Integration by Substitution	Definition--Calculus Topics--Integration by Substitution Topic Calculus Definition Integration by substitution is a method used to evaluate integrals by substituting a new variable for a part of the integrand, often simplifying the integral. Description Integration by substitution is a fundamental technique in calculus, often considered the counterpart to the chain rule for derivatives. It's particularly useful for integrating composite functions and functions involving trigonometric, exponential, or logarithmic terms. This method is widely applied in physics and engineering to solve problems involving changing variables or coordinate systems.	Calculus Vocabulary
Definition--Calculus Topics--Rational Function	Definition--Calculus Topics--Rational Function Topic Calculus Definition A rational function is a function that can be expressed as the ratio of two polynomials, P(x)/Q(x), where Q(x) ≠ 0. Description Rational functions are a crucial class of functions in calculus and algebra, with wide-ranging applications in science, engineering, and economics. They exhibit interesting behaviors such as asymptotes, holes, and discontinuities, making them valuable for modeling complex real-world phenomena. The study of rational functions involves analyzing their domain, range, intercepts, and end behavior.	Calculus Vocabulary
Definition--Rationals and Radicals--Fourth Root	Fourth Root Topic Rationals and Radicals Definition The fourth root of a number is a value that, when raised to the power of four, gives the original number. Description The fourth root is an important concept in Radical Numbers, Expressions, Equations, and Functions. It is the inverse operation of raising a number to the power of four. Understanding fourth roots is crucial for solving higher-degree equations and for simplifying radical expressions. Fourth roots are also relevant in various scientific and engineering applications where higher-degree roots are required. They are a part of advanced mathematical studies, including algebra and calculus.	Radical Expressions
Definition--Rationals and Radicals--Geometric Mean	Geometric Mean Topic Rationals and Radicals Definition The geometric mean of two numbers is the square root of their product. Description The geometric mean is an example of using radical expressions to solve a problem. It provides a measure of central tendency that is particularly useful in situations where the numbers are multiplied together rather than added. In geometry, the geometric mean appears in various theorems and constructions. It is also used in finance and statistics to calculate average growth rates and to compare different sets of data.	Radical Expressions
Definition--Rationals and Radicals--Rationalizing the Denominator	Rationalizing the Denominator Topic Rationals and Radicals Definition Rationalizing the denominator is the process of eliminating radicals or complex numbers from the denominator of a fraction by multiplying both the numerator and denominator by an appropriate factor. Description Rationalizing the Denominator is a crucial technique in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves removing radicals or complex numbers from the denominator of a fraction, which simplifies the expression and often makes it easier to evaluate or compare with other expressions. For example, to rationalize the denominator of	Radical Expressions
Definition--Rationals and Radicals--Conjugate of a Radical	Conjugate of a Radical Topic Rationals and Radicals Definition The conjugate of a radical expression is obtained by changing the sign between two terms in a binomial. Description In the context of Radical Numbers, Expressions, Equations, and Functions, the concept of conjugates is essential for simplifying expressions. When dealing with radicals, particularly in the denominator, multiplying by the conjugate can help to rationalize the expression. This process eliminates the radical from the denominator, making the expression easier to work with.	Radical Expressions
Definition--Rationals and Radicals--Rationalizing a Radical	Rationalizing a Radical Topic Rationals and Radicals Definition Rationalizing a radical is the process of eliminating radicals from the denominator of a fraction by multiplying both the numerator and denominator by an appropriate factor. Description Rationalizing a Radical is an important technique in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves eliminating radicals from the denominator of a fraction, which simplifies the expression and often makes it easier to work with or compare to other expressions. For example, to rationalize the denominator of $\frac{1}{\sqrt{3}}$	Radical Expressions
Definition--Rationals and Radicals--Simplifying a Radical Expression	Simplifying a Radical Expression Topic Rationals and Radicals Definition Simplifying a radical expression involves reducing the expression to its simplest form by factoring the radicand and removing any perfect square factors (for square roots) or perfect cube factors (for cube roots). Description Simplifying a Radical Expression is a fundamental skill in the study of Radical Numbers, Expressions, Equations, and Functions. This process involves reducing a radical expression to its simplest form, which often makes it easier to work with and understand. For example, simplifying $\sqrt{18}$ results in	Radical Expressions
Definition--Rationals and Radicals--Rational Exponent	Rational Exponent Topic Rationals and Radicals Definition A rational exponent is an exponent that is a fraction, where the numerator indicates the power and the denominator indicates the root. Description Rational Exponents are a crucial concept in the study of Rational Numbers, Expressions, Equations, and Functions. These exponents are fractions, where the numerator indicates the power and the denominator indicates the root. For example, the expression $a^{m/n}$ can be rewritten as $\sqrt[n]{a^m}$	Rational Expressions
Definition--Rationals and Radicals--Laws of Rational Exponents	Laws of Rational Exponents Topic Rationals and Radicals Definition The laws of rational exponents describe how to handle exponents that are fractions, including rules for multiplication, division, and raising a power to a power. Description The Laws of Rational Exponents are vital in the study of Rational Numbers, Expressions, Equations, and Functions. These laws provide a framework for simplifying expressions involving exponents that are fractions. For example, the law $a^{m/n} = \sqrt[n]{a^m}$	Rational Expressions
Definition--Rationals and Radicals--Factoring a Radical	Factoring a Radical Topic Rationals and Radicals Definition Factoring a radical involves expressing it as a product of simpler expressions. Description Factoring radicals is a key technique in the study of Radical Numbers, Expressions, Equations, and Functions. It simplifies complex radical expressions, making them easier to work with. This process is essential for solving equations and for performing algebraic manipulations involving radicals. Understanding how to factor radicals is also important for simplifying expressions in calculus and higher-level mathematics. It helps in breaking down complex problems into more manageable parts.	Radical Functions and Equations
Definition--Rationals and Radicals--Simplifying a Rational Expression	Simplifying a Rational Expression Topic Rationals and Radicals Definition Simplifying a rational expression involves reducing the fraction to its lowest terms by factoring both the numerator and denominator and canceling common factors. Description Simplifying a Rational Expression is a crucial skill in the study of Rational Numbers, Expressions, Equations, and Functions. This process involves reducing a rational expression to its simplest form by factoring both the numerator and denominator and canceling common factors. For example, simplifying $\frac{x^2 - 1}{x - 1}$ results in x + 1 for	Rational Expressions
Definition--Rationals and Radicals--Partial Fraction Decomposition of a Rational Expression	Partial Fraction Decomposition of a Rational Expression Topic Rationals and Radicals Definition Partial fraction decomposition is a method used to express a rational expression as a sum of simpler fractions. Description Partial Fraction Decomposition is a powerful tool in the study of Rational Numbers, Expressions, Equations, and Functions. It involves breaking down a complex rational expression into a sum of simpler fractions, which are easier to integrate or differentiate. For example, the rational function $\frac{2x+3}{(x+1)(x-2)}$ can be decomposed into	Rational Expressions
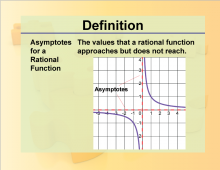
Definition--Rationals and Radicals--Asymptotes for a Rational Function	Asymptotes for a Rational Function Topic Rationals and Radicals Definition An asymptote is a line that a graph approaches but never touches. Description Asymptotes are significant in the study of Rational Numbers, Expressions, Equations, and Functions. They help in understanding the behavior of graphs of rational functions, particularly as the values of the variables approach certain limits. Horizontal asymptotes indicate the value that the function approaches as the input grows infinitely large or small. Vertical asymptotes show the values that the function cannot take because they cause division by zero.	Rational Functions and Equations
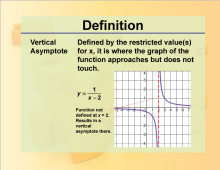
Definition--Rationals and Radicals--Vertical Asymptote	Vertical Asymptote Topic Rationals and Radicals Definition A vertical asymptote is a vertical line that the graph of a function approaches but never reaches as the input values get closer to a certain point. Description Vertical Asymptotes are a crucial concept in the study of Rational Numbers, Expressions, Equations, and Functions. They occur in rational functions when the denominator equals zero for certain input values, causing the function to approach infinity or negative infinity. For example, the function $f(x) = \frac{1}{x-2}$	Rational Functions and Equations
Definition--Rationals and Radicals--Horizontal Asymptote	Horizontal Asymptote Topic Rationals and Radicals Definition A horizontal asymptote is a horizontal line that a rational function graph approaches as the input values become very large or very small. Description Horizontal asymptotes are an important concept in the study of Rational Numbers, Expressions, Equations, and Functions. They indicate the value that a function approaches as the input grows infinitely large or small. Understanding horizontal asymptotes is crucial for graphing rational functions accurately and for analyzing their long-term behavior.	Rational Functions and Equations
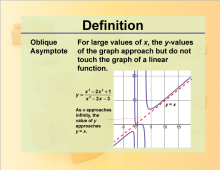
Definition--Rationals and Radicals--Oblique Asymptote	Oblique Asymptote Topic Rationals and Radicals Definition An oblique asymptote is a diagonal line that the graph of a function approaches as the input values become very large or very small. Description Oblique Asymptotes are important in the study of Rational Numbers, Expressions, Equations, and Functions. They occur in rational functions where the degree of the numerator is one more than the degree of the denominator. For example, the function $f(x) = \frac{x^2 + 1}{x}$	Rational Functions and Equations
Definition--Rationals and Radicals--Rational Equations	Rational Equations Topic Rationals and Radicals Definition Rational equations are equations that involve rational expressions, which are fractions containing polynomials in the numerator and denominator. Description Rational Equations are a fundamental aspect of Rational Numbers, Expressions, Equations, and Functions. These equations involve rational expressions, which are fractions containing polynomials in the numerator and denominator. Solving rational equations typically requires finding a common denominator, clearing the fractions, and then solving the resulting polynomial equation. For example, to solve $\frac{1}{x} + \frac{1}{x+1} = \frac{1}{2}$	Rational Functions and Equations
Definition--Rationals and Radicals--Radical Equations	Radical Equations Topic Rationals and Radicals Definition Radical equations are equations in which the variable is inside a radical, such as a square root or cube root. Description Radical Equations are a fundamental aspect of Radical Numbers, Expressions, Equations, and Functions. These equations involve variables within radical signs, such as square roots or cube roots. Solving radical equations typically requires isolating the radical on one side of the equation and then squaring both sides to eliminate the radical. For example, to solve $\sqrt{x+3} = 5$ one would square both sides to obtain $x + 3 = 25$	Radical Functions and Equations
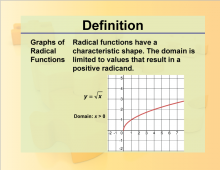
Definition--Rationals and Radicals--Graphs of Radical Functions	Graphs of Radical Functions Topic Rationals and Radicals Definition Graphs of radical functions are visual representations of equations involving radicals. Description Graphs of radical functions are crucial in the study of Radical Numbers, Expressions, Equations, and Functions. They provide a visual understanding of how these functions behave, including their domains, ranges, and key features such as intercepts and asymptotes.	Radical Functions and Equations
Math Example--Polynomial Concepts-- Rational Root Theorem: Example 7	Math Example--Polynomial Concepts-- Rational Root Theorem: Example 7 Topic Polynomials	Factoring Polynomials
Math Example--Polynomial Concepts-- Rational Root Theorem: Example 6	Math Example--Polynomial Concepts-- Rational Root Theorem: Example 6 Topic Polynomials Description The example illustrates the process of finding rational roots for the polynomial. Find the rational roots of the polynomial P(x) = x3 - 3x2 + 7x - 5 using the Rational Root Theorem. 1. Identify factors of the constant term (-5), which are ±1 and ±5, and factors of the leading coefficient (1), which is ±1. 2. Form possible values of p/q: ±1 and ±5. 3. Test these values to find the roots. Roots found are x = 1. 4. The polynomial can be factored as P(x) = (x - 1)(x2 - 2x + 5). The answer is P(x) = (x - 1)(x2 - 2x + 5). There are no additional rational roots.	Factoring Polynomials
Math Example--Polynomial Concepts-- Rational Root Theorem: Example 5	Math Example--Polynomial Concepts-- Rational Root Theorem: Example 5 Topic Polynomials Description The example illustrates the process of finding rational roots for the polynomial. Find the rational roots of the polynomial P(x) = 3x3 - 7x2 + 4 using the Rational Root Theorem. 1. Identify factors of the constant term (4), which are ±1, ±2, and ±4, and factors of the leading coefficient (3), which are ±1 and ±3. 2. Form possible values of p/q: ±1/3, ±2/3, ±1, ±4/3, ±2, and ±4. 3. Test these values to find the roots. Roots found are x = -2/3, 1, and 2. 4. The polynomial can be factored as P(x) = 3x3 - 7x2 + 4. The answer is P(x)=(x + 2/3)(x - 1)(x - 2).	Factoring Polynomials
Math Example--Polynomial Concepts-- Rational Root Theorem: Example 4	Math Example--Polynomial Concepts-- Rational Root Theorem: Example 4 Topic Polynomials	Factoring Polynomials
Math Example--Polynomial Concepts-- Rational Root Theorem: Example 3	Math Example--Polynomial Concepts-- Rational Root Theorem: Example 3 Topic Polynomials Description The example illustrates the process of finding rational roots for the polynomial. Find the rational roots of the polynomial P(x) = x3 - 7x2 + 14x - 8 using the Rational Root Theorem. 1. Identify possible factors of the constant term (-8), which are ±1, ±2, ±4, and ±8. 2. Test each factor by substituting them into the polynomial until a root is found. Roots found are x = 1, 2, and 4. 3. The polynomial can be factored as P(x)=(x - 1)(x - 2)(x - 4). The answer is P(x) = x3 - 7x2 + 14x - 8.	Factoring Polynomials
Math Example--Polynomial Concepts-- Rational Root Theorem: Example 2	Math Example--Polynomial Concepts-- Rational Root Theorem: Example 2 Topic Polynomials Description The example illustrates the process of finding rational roots for the polynomial. Find the rational roots of the polynomial P(x) = x3 + 7x2 + 14x + 8 using the Rational Root Theorem. 1. Identify possible factors of the constant term (8), which are ±1, ±2, ±4, and ±8. 2. Test each factor by substituting them into the polynomial to find the roots. Roots found are x = -1, -2, and -4. 3. The polynomial can be factored as P(x) = x3 + 7x2 + 14x + 8. The answer is P(x) = (x + 1)(x + 2)(x + 4).	Factoring Polynomials
Math Example--Polynomial Concepts-- Rational Root Theorem: Example 1	Math Example--Polynomial Concepts-- Rational Root Theorem: Example 1 Topic Polynomials Description The example illustrates the process of finding rational roots for the polynomial. Find the rational roots of the polynomial P(x) = x3 + 4x2 + x - 6 using the Rational Root Theorem. 1. Identify possible factors of the constant term (-6), which are ±1, ±2, ±3, and ±6. 2. Test each factor as possible roots by substituting them into the polynomial until a root is found. Roots found are x = 1, -2, and -3. 3. The polynomial can be factored as P(x) = x3 + 4x2 + x - 6. The answer is P(x)=(x - 1)(x + 2)(x + 3).	Factoring Polynomials
Definition--Polynomial Concepts--Rational Root Theorem	Rational Root Theorem Topic Polynomials Definition The Rational Root Theorem states that any rational root of a polynomial equation is a factor of the constant term divided by a factor of the leading coefficient. Description The Rational Root Theorem is a powerful tool in algebra that provides a systematic way to identify possible rational roots of a polynomial equation. According to the theorem, any rational root of a polynomial equation is a factor of the constant term divided by a factor of the leading coefficient. This theorem is particularly useful for solving higher-degree polynomial equations and for analyzing polynomial functions.	Factoring Polynomials
Video Tutorial: Ratios, Video 20	Video Tutorial: Ratios and Rates: Rate of Change This is part of a collection of video tutorials on the topic of Ratios and Proportions. This series includes a complete overview of ratios, equivalent ratios, rates, unit rates, and proportions. The following section will provide additional background information for the complete series of videos. What Are Ratios? A ratio is the relationship between two or more quantities among a group of items. The purpose of a ratio is find the relationship between two or more items in the collection. Let's look at an example.	Point-Slope Form and Slope